Метод секущих (метод хорд)

При решении уравнения (1.1) методом Ньютона иногда возникают сложности при взятии производной функции в формуле (1.2). Это случается, например, когда функция 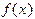не имеет конкретного вида, а получается из предварительных вычислений или же принимает очень сложную форму. Тогда часто применяют метод секущих. Если в формуле (1.2) заменить 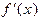приближенным выражением , то получится расчетная формула для двухшагового метода секущих:

. (1.3)

Метод называется двухшаговым, так как требуется не одно, а два начальных приближения: 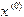и 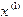. Далее, как видно из формулы (1.3), для получения каждого последующего приближения требуется два предыдущих. На практике чаще применяется одношаговый метод - модификация формулы (1.3). Одношаговый метод часто называют методом хорд (хотя терминология здесь не устоялась - в разных учебниках называют этот метод по-разному). Пусть , функция 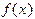принимает на концах отрезка 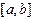значения разных знаков. Тогда, как мы знаем, существует корень 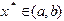уравнения (1.1), причем он единственный в случае, когда 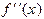не меняет знак. Это обстоятельство объясняет применение одношагового метод секущих:

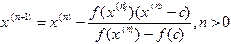. (1.4)

Здесь c равно либо a, либо b, в зависимости от знака функции 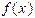и знака ее второй производной (выбирается тот конец отрезка, где знак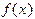и и 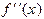совпадают). На рис.4 показаны четыре возможных варианта:

Рис.4

В качестве начального приближения 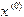принимают точку a (рис.4 а,г) или точку b (рис.4 б,в). Тогда, согласно формуле (1.4), следующим приближением станет абсцисса точки пересечения отрезка секущей (хорды) с осью Ox. Это хорошо иллюстрирует рис.4.