Порядок расчета геометрических характеристик плоских сечений
Рекомендуется следующий порядок определения геометрических характеристик сложных составных сечений:
1. Выбираем начальную систему координат y0z0, проводя оси y0 и z0 так, чтобы они касались крайних точек составного сечения слева и снизу (см. рис. 4.2а).
2. Сложную фигуру разбиваем на простые (F1, F2 и т.д.), характеристики которых легко определить. Если в составное сечение входят прокатные профили (уголки, швеллера и т.п.), то необходимые геометрические характеристики их (площадь сечения, положение центра тяжести и др.) выбираются по таблице сортамента.
3. В выбранной системе координат определяем положение центров тяжести простых фигур, обозначая их соответственно как C1(y1,z1), C2(y2,z2) и т.д. (рис. 4.2б) Символом F1, F2 и т. д., будем обозначать не только порядковый номер фигуры, но и площадь её сечения.
2. По формулам (4.8) определяем координаты центра тяжести фигуры C(yс,zс) и проводим центральные оси y и z (рис. 4.2б). Определяем моменты инерции частей фигуры относительно их собственных центральных осей (y1,z1 , y2,z2 и т.д.), и размеры а1, b1, а2, b2 и др. Используя формулы перехода к параллельным осям – (4.9)…(4.11) вычисляем значения 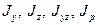 .
.
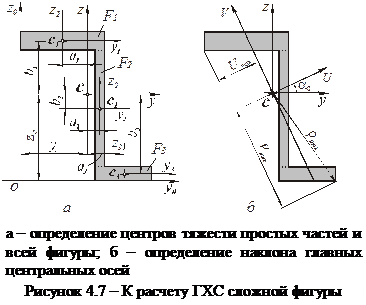
5. По формуле (4.13), определяем угол наклона главных центральных осей, причем ось, проведенную под меньшим углом (положительным или отрицательным), обозначаем буквой U,а перпендикулярную к ней – буквойV.
6. По формулам (4.14) определяем значения главных центральных моментов инерции.
Пример 4.1.
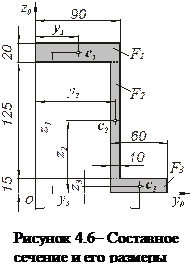
Для Z – образного сечения, показанного на рис. 4.6, определить положение центра тяжести yc, zc , угол наклона главных центральных осей инерции 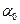 , моменты инерции относительно центральных осей oy и oz и моменты инерции относительно главных центральных осей U и V.
, моменты инерции относительно центральных осей oy и oz и моменты инерции относительно главных центральных осей U и V.
Р е ш е н и е.
Выберем систему начальных осей y0 и z0, проведя их так, чтобы они касались крайних точек (слева и снизу) рассматриваемого составного сечения.
Разбиваем фигуру на простые части в виде прямоугольников, находим площади их сечений и общую площадь фигуры:
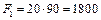 мм2 ,
мм2 , 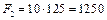 мм2,
мм2, 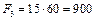 мм2,
мм2,
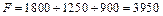 мм2.
мм2.
В выбранной системе осей определяем координаты центров тяжести простых фигур – C1, C2, C3, обозначая их соответственно как y1, z1; y2, z2 и т.д. (рис. 4.6). В таблице 4.1 даются численные значения искомых величин.
Координаты центра тяжести yс, zс составной фигуры в системе y0z0, определяем по формулам (4.8):
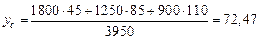 мм
мм
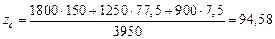 мм,
мм,
Таблица 4.1 – Промежуточные параметры сечения
| Фигура | Площадь фигуры, мм2 | Координаты ЦТ фигуры в системе y0z0, мм | Координаты ЦТ фигуры в центральной системе yz, мм | Статический момент площади фигуры относительно осей y0 и z0, 104 мм3 | Координаты ЦТ всей фигуры в системе y0z0, мм | ||||
| yi | zi | ai | bi | 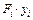
| 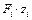
| yс | zс | ||
| F1 | -27,46 | 55,42 | 8,1 | ||||||
| F2 | 77,5 | 12,54 | -17,08 | 10,62 | 9,7 | ||||
| F3 | 7,5 | 37,54 | -87,08 | 9,9 | 0,67 | ||||
| F | - | - | - | - | 28,62 | 37,37 | 72,47 | 94,58 |
Определим моменты инерции каждого прямоугольника относительно собственных центральных осей:
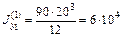 мм4,
мм4, 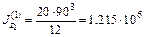 мм2.
мм2.
Остальные значения моментов (размерность – мм4) приводим без подробностей расчета:
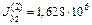 ,
, 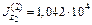 ,
, 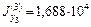 ,
, 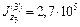 .
.
Моменты инерции каждой простой фигуры относительно центральных осей y и z вычисляются по формулам (4.11). Например:
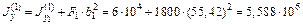 мм4,
мм4,
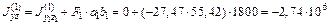 мм4.
мм4.
Остальные значения моментов приводим без подробностей расчета в таблице 4.2.
Суммируя последние три столбца таблицы 4.2, находим моменты инерции составной фигуры относительно центральных осей y и z :

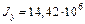 мм4,
мм4, 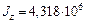 мм4,
мм4, 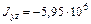 мм4.
мм4.
Угол наклона главных центральных осей (рис. 4.7б) к оси oy найдем по формуле (4.13):
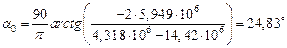 .
.
Таблица 4.2 – Моменты инерции сечения
| Фигура | Моменты инерции фигуры,
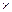 106 мм4,
относительно 106 мм4,
относительно
| ||||
| собственных осей yi, zi | центральных осей y; z | ||||
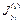
| 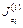
| 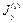
| 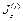
| 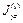
| |
| F1 | 0,06 | 1,215 | 5,588 | 2,573 | -2,74 |
| F2 | 1,628 | 0,0104 | 1,993 | 0,207 | -0,267 |
| F3 | 0,0168 | 0,27 | 6,842 | 1,538 | -2,941 |
Примечание: Центробежные моменты инерции фигур относительно собственных центральных осей 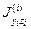 = 0
= 0
Главные центральные моменты инерции (мм4) определяем по формулам (4.14):
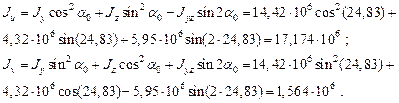
Правильность расчетов проверяем по условию (4.17):
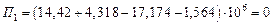 ,
,
что указывает на достаточную точность полученных результатов.
Реальные конструктивные элементы сварных конструкций (балки, фермы, колонны и т.д.) могут включать в себя как стандартные профили (уголки, швеллера, двутавры), так и нестандартные виды сечений простого или сложного очертания. Приводим пример, в котором рассматривается составное сечение, включающее профильный элемент в виде неравнополочного уголка.
Пример 4.2.
Найти положение главных центральных осей и значения главных центральных моментов инерции для сечения состоящего из неравнополочного уголка сечением 110 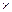 70
70 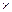 8 мм (ГОСТ 8510-86) и прямоугольной полосы сечением 20
8 мм (ГОСТ 8510-86) и прямоугольной полосы сечением 20 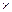 160 мм (рис. 4.8).
160 мм (рис. 4.8).
Р е ш е н и е
Прежде всего, определим все необходимые параметры сечения стандартного уголка. По сортаменту прокатной угловой стали, устанавливаем координаты ЦТ уголка (рис. 4.8,а) и значение необходимых ГХС:
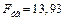 см2,
см2, 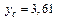 см,
см, 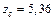 см,
см, 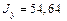 см4,
см4,
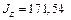 см4,
см4, 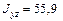 см4,
см4, 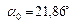 .
.
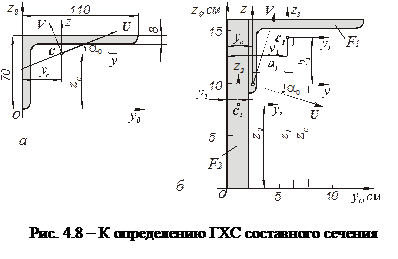
В выбранной системе осей составного сечения (рис. 4.8б) определяем координаты центров тяжести простых фигур – C1, C2,, обозначая их соответственно как y1, z1; y2, z2. В таблице 4.3 даются численные значения искомых величин.
Координаты центра тяжести yс, zс составной фигуры в системе y0z0, определяем по формулам (4.8):
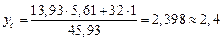 cм,
cм,
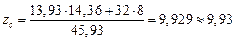 cм.
cм.
Таблица 4.3 –Промежуточные параметры сечения (рис. 4.8б)
| Фигура | Площадь фигуры, см2 | Координаты ЦТ фигуры в системе y0z0, см | Координаты ЦТ фигуры в центральной системе yz, см | Статический момент площади фигуры относительно осей
y0 и z0,
 104 см3 104 см3
| Координаты ЦТ всей фигуры в системе y0z0, см | ||||
| yi | zi | ai | bi | 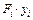
| 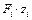
| yс | zс | ||
| F1 | 13,93 | 5,61 | 14,36 | 3,212 | 4,431 | 0,781 | 2,0 | ||
| F2 | -1,398 | -1,929 | 0,32 | 2,56 | |||||
| F | 45,93 | - | - | - | - | - | - | 2,4 | 9,93 |
Поскольку моменты инерции уголка уже известны, то определим их только для полосы (вторая простая фигура – F2) относительно собственных центральных осей:
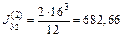 см4,
см4, 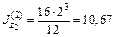 см2.
см2.
Моменты инерции (см4) каждой фигуры относительно центральных осей y и z вычисляются по формулам (4.11):
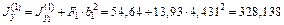 ,
,
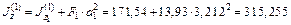 ,
,
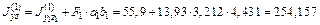 .
.
Остальные значения моментов (см4) приводим без подробностей расчета:
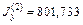 ,
, 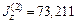 ,
, 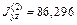
Суммируя составляющие (см. формулы 4.9 и 4.10), находим моменты инерции составной фигуры относительно центральных осей y и z :
Угол наклона главных центральных осей (рис. 4.8,б) к оси oy найдем по формуле (4.13):
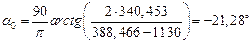 .
.
Главные центральные моменты инерции (см4) определяем по формулам (4.14):
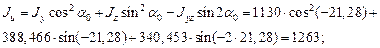
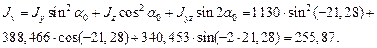
Пример 4.3.
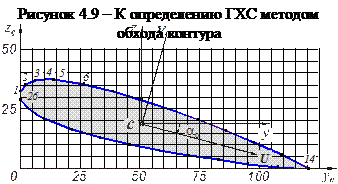
Определить геометрические характеристики поперечного сечения сварной лопасти руля судна, ( рис. 4.9) ось которой наклонена под углом 15 градусов к оси движения судна. Профиль лопасти задан координатами 26 точек в таблице 4.4 (в наклоненном положении). Размеры заданы в см.
Р е ш е н и е
Поскольку сечение рулевой лопасти имеет сложное очертание и его нельзя расчленить на простые фигуры, воспользуемся вторым способом определения ГХС – способом обхода контура, используя формулы (4.16).
Таблица 4.4 – Координаты точек контура лопасти руля (см)
| y | 0,0 | 1,97 | 6,4 | 10,65 | 14,24 | 26,67 | 38,81 | 50,78 | 62,64 |
| z | 32,35 | 35,29 | 36,95 | 37,33 | 37,21 | 35,32 | 32,3 | 28,7 | 24,65 |
| y | 74,43 | 86,14 | 97,8 | 109,37 | 120,74 | 107,96 | 95,39 | 82,89 | 70,45 |
| z | 20,36 | 15,77 | 10,94 | 5,87 | 0,0 | 0,59 | 1,99 | 3,64 | 5,52 |
| y | 58,09 | 45,8 | 33,63 | 21,62 | 9,9 | 6,73 | 3,25 | 0,24 | - |
| z | 7,69 | 10,11 | 12,98 | 16,44 | 21,02 | 22,71 | 25,16 | 28,82 | - |
По заданным координатам точек контура (на рис. 4.9 точки обозначены цифрами 1…26, обход сделан по часовой стрелке) определяем, вначале, значения промежуточной величины 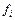 для каждой пары координат рассматриваемой точки, например, для точки 5 (
для каждой пары координат рассматриваемой точки, например, для точки 5 ( 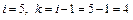 ):
):
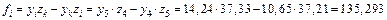 .
.
Всего будет двадцать шесть значений 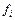 .
.
Далее определяем: площадь сечения лопасти F, координаты центра тяжести (в координатной системе y00z0) сечения 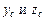 , моменты инерции
, моменты инерции 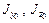 и центробежный момент
и центробежный момент 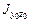 .
.
Выполненные расчеты дают следующие величины:
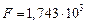 см2,
см2, 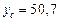 см,
см, 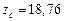 см,
см, 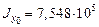 см4,
см4, 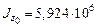 см4,
см4, 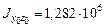 см2.
см2.
Моменты инерции относительно центральных осей 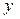 и
и 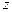 , а также главные центральные осевые моменты инерции и их положение (угол
, а также главные центральные осевые моменты инерции и их положение (угол 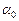 ) определяются по ранее рассмотренным соотношениям:
) определяются по ранее рассмотренным соотношениям:
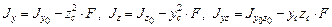 и т.д.
и т.д.
Выполненные расчеты дают следующие величины:
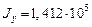 см4,
см4, 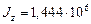 см4,
см4, 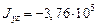 см4,
см4,
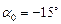 ,
, 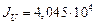 см4,
см4, 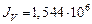 см4,
см4,
В заключение отметим, что расчеты по второму методу целесообразно выполнять на компьютере по составленной программе или используя известный математический редактор, например – MathСad.
Дата добавления: 2018-11-26; просмотров: 1666;











