Построение эпюр внутренних сил в сечениях типовых элементов конструкций
При всем разнообразии конструктивных форм, встречающихся в сооружениях и машинах, их можно свести к комбинации стержневых (балки, стойки, валы) и листовых (пластинки, оболочки) элементов (рис. 4.16).
Наиболее распространенными типовыми элементами конструкций являются балки. Балками называют прямолинейные стержни, работающие на изгиб.
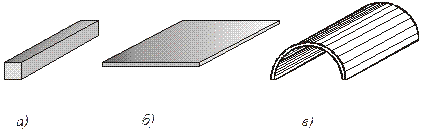
Рисунок 4.16 – Основные типы элементов конструкций: стержень (а); пластина (б); оболочка (в)
При расчете балку принято заменять осью (рис. 4.17), а опорные устройства балок схематизируются одной из трех видов опор: шарнирно-неподвижная (опора А), шарнирно-подвижная (опора В) и защемление (заделка).
 |
Для построения эпюр внутренних сил необходимо знать все внешние нагрузки, включая реакции, которые могут быть определены по формулам (4.13).
При определении опорных реакций распределенную нагрузку заменяют равнодействующей. Если в результате вычисления какая-либо реакция окажется отрицательной, то это указывает на неверный выбор направления ее и оно должно быть изменено[1].
Поперечной силой ( 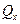 )в данном сечении называется сумма проекций всех внешних сил, находящихся по одну сторону от сечения, на нормаль к оси балки.
)в данном сечении называется сумма проекций всех внешних сил, находящихся по одну сторону от сечения, на нормаль к оси балки.
Изгибающим моментом (Мх)в данном сечении называется сумма моментов всех внешних сил, находящихся по одну сторону от сечения, относительно центра тяжести этого сечения.
При построении эпюр поперечных сил 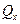 и изгибающих моментов Мх принимают следующие правила знаков:
и изгибающих моментов Мх принимают следующие правила знаков:
– изгибающий момент Мх в сечении положителен, если он вызывает сжатие в верхних волокнах балки.
– поперечная сила 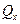 в сечении положительна, если ее векторы стремятся вращать части рассеченной балки по часовой стрелке; Эти правила знаков, отражаются на рис. 4.18.
в сечении положительна, если ее векторы стремятся вращать части рассеченной балки по часовой стрелке; Эти правила знаков, отражаются на рис. 4.18.

Изгибающий момент, поперечная сила и интенсивность распределенной нагрузки связаны между собой следующими зависимостями (по Д. И. Журавскому):

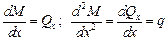 . (4.16)
. (4.16)
Эти соотношения называют дифференциальными зависимостями при изгибе. Они позволяют установить некоторые правила построения эпюр поперечных сил и изгибающих моментов (см. таблицу 4.5):
 |
Таблица 4.5 – Построение эпюр по характерным точкам
1. В сечениях, где к балке приложены сосредоточенные силы (включая и опорные реакции), на эпюре поперечных сил будут скачки.
2. В сечениях, где приложены сосредоточенные моменты, эпюра поперечных сил не меняется, а на эпюре Мх наблюдается скачок на величину сосредоточенных моментов.
3. На тех участках, где нет распределенной нагрузки, эпюра 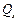 ограничена прямыми, параллельными оси, а эпюра Мх – наклонными прямыми.
ограничена прямыми, параллельными оси, а эпюра Мх – наклонными прямыми.
2. Если на участке действует равномерно распределенная нагрузка, то эпюра Мх ограничена квадратичной параболой, а эпюра Qx –, наклонными прямыми. При этом в сечениях, где 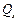 меняет знак (
меняет знак ( 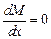 ), изгибающий момент достигает максимума или минимума.
), изгибающий момент достигает максимума или минимума.
Пример 4.4.
Для заданных размеров балки и схемы приложения нагрузок (рис. 4.17), построить эпюры поперечных сил 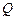 и изгибающих моментов М.
и изгибающих моментов М.
Исходные данные:
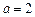 м;
м; 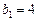 м;
м; 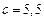 м;
м; 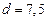 м;
м; 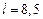 м;
м; 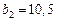 м;
м;
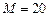 кНм;
кНм; 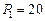 кН;
кН; 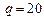 кН/м;
кН/м; 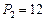 кН.
кН.
Р е ш е н и е.
1. Определение опорных реакций.
Направим реакции RA, и RB вверх. Составим уравнение моментов относительно точки А:
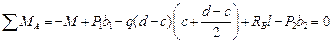 .
.
Отсюда, подставив числовые значения, находим RB:
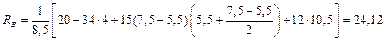 кН.
кН.
Составим уравнение моментов относительно точки В:
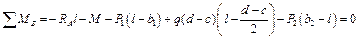 .
.

Откуда, подставив числовые значения, находим RА (кН):
Для проверки правильности определения реакций составляем сумму проекций всех сил на ось y:
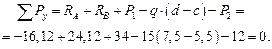
Таким образом, реакции определены верно.
Обратим внимание, что реакция RА получилась отрицательной, поэтому, в дальнейшем необходимо изменить на рисунке её направление на обратное (см. рис. 4.19) и считать эту реакцию положительной. С учетом сказанного принимаем RA = 16,12 кН.
 |
2. Построение эпюр поперечных сил и изгибающих моментов.
Для построения эпюр Q и M используем метод сечений.
Балка имеет шесть участков, поэтому будем рассматривать условие равновесия отсекаемой части балки поочередно на каждом участке. Напомним, что поперечная сила 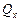 в произвольном поперечном сечении бруса с абсциссой х равна алгебраической сумме проекций на ось y всех внешних сил, приложенных к его отсеченной части.
в произвольном поперечном сечении бруса с абсциссой х равна алгебраической сумме проекций на ось y всех внешних сил, приложенных к его отсеченной части.
Изгибающий момент 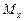 в этом же сечении, равен алгебраической сумме моментов всех сил, приложенных к отсеченной части, относительно той точки оси бруса, через которую проходит рассматриваемое сечение (точка С на рисунке 4.19).
в этом же сечении, равен алгебраической сумме моментов всех сил, приложенных к отсеченной части, относительно той точки оси бруса, через которую проходит рассматриваемое сечение (точка С на рисунке 4.19).
На первом участке для любого сечения х (0 ≤ x ≤ а) запишем:
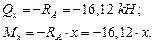
При 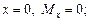
При 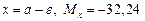 кНм.
кНм.
Здесь 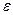 бесконечно малая величина, позволяющая определить значение момента в сечении, расположенном весьма близко к границе I – го участка. Это необходимо сделать, чтобы при переходе через границу участка обнаружить скачек момента, поскольку в сечении
бесконечно малая величина, позволяющая определить значение момента в сечении, расположенном весьма близко к границе I – го участка. Это необходимо сделать, чтобы при переходе через границу участка обнаружить скачек момента, поскольку в сечении 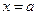 приложен внешний сосредоточенный момент М. Из последнего выражения видно, что
приложен внешний сосредоточенный момент М. Из последнего выражения видно, что 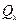 не зависит от х, т.е. она постоянная на длине участка, а
не зависит от х, т.е. она постоянная на длине участка, а 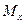 являетсялинейной функцией х , поэтому на первом участке построить эпюры достаточно просто.
являетсялинейной функцией х , поэтому на первом участке построить эпюры достаточно просто.
На втором участке (см. рис. 4.19) для любого сечения х (а ≤ x ≤ b1) запишем:
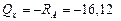 кН;
кН;
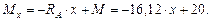
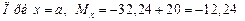 кНм;
кНм;
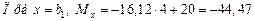 кНм.
кНм.
Рассмотрим еще один участок – четвертый (см. рис. 4.19) на котором имеется распределенная нагрузка q. Поперечная сила в сечении х от действия только распределенной нагрузки численно равна равнодействующей 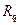 распределенной нагрузки на длине
распределенной нагрузки на длине 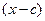 , т.е.
, т.е. 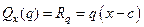 . Изгибающий момент в том же сечении от q равен моменту их равнодействующей
. Изгибающий момент в том же сечении от q равен моменту их равнодействующей 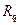 , линия действия которой проходит посредине отрезка
, линия действия которой проходит посредине отрезка 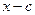 , т.е.
, т.е.
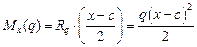 .
.
С учетом сказанного составим полное уравнение равновесия для отсеченной части при расположении сечения с абсциссой х на четвертом участке ( 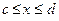 ):
):
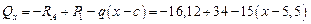 кН,
кН,
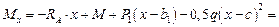
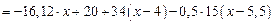 кНм.
кНм.
Анализ последнего выражения показывает, что поперечная силалинейно зависит от х, поэтому для построения эпюры 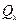 достаточно найти ее ординаты в двух граничных сечениях: x = c и x = d.
достаточно найти ее ординаты в двух граничных сечениях: x = c и x = d.
При 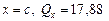 кН; при
кН; при 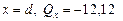 кН.
кН.
В тоже время, изгибающий момент в пределах длины четвертого участка, изменяется по квадратичному закону, поэтому для построения эпюры 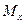 следует определить три-четыре её ординаты. Изгибающие моменты на границах участка:
следует определить три-четыре её ординаты. Изгибающие моменты на границах участка:
при 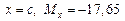 кНм;
кНм;
при 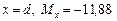 кНм.
кНм.
Для приближенного построения параболы необходимо определить ординату эпюры Мх, соответствующую экстремальной величине М. Для этого нужно найти координату сечения, в котором Q = 0. В соответствии с полученными выше формулами запишем:
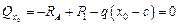 ,
,
откуда
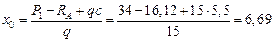 м.
м.
тогда
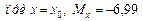 кНм.
кНм.
Порядок построения эпюр на других участках выполняется по таким же правилам.
 |
На рисунке 4.20 показаны эпюры поперечных сил и изгибающих моментов для рассматриваемой балки.
При построении эпюр внутренних усилий в колоннах следует учесть, что помимо поперечных сил Qx и изгибающих моментов Мх в сечениях колонны будут действовать и продольные силы. В данном поперечном сечении продольная сила равна сумме проекций всех сил, расположенных по одну сторону от этого сечения, на ось бруса (на нормаль к сечению).
Продольная сила, направленная от сечения (растяжение), считается положительной, а направленная к сечению (сжатие) – отрицательной (рис. 4.21). В том случае, когда направление продольной силы заранее неизвестно, ее направляют от сечения. Если из условия равновесия ( 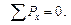 ) продольная сила получится со знаком плюс, стержень в данном случае испытывает растяжение, со знаком минус – сжатие.
) продольная сила получится со знаком плюс, стержень в данном случае испытывает растяжение, со знаком минус – сжатие.

Наглядное представление о методике построения эпюр и характере распределения внутренних сил в колонне дает рис. 4.21. Линейные размеры колонны и величины нагрузок взяты такими: а = 8 м; b = 7 м; с = 5 м; е = 0,5 м; Р1 = 200 кН; Р2 = 20 кН; Р3 = 100 кН; Р4 = 10 кН; Р5 = 50 кН.
Контрольные вопросы к лекции № 4
1. Как классифицируются нагрузки, действующие на части машин и сооружений?
2. Что называется брусом, пластинкой и тонкостенной оболочкой?
3. Какие основные виды деформаций вызываются внешними силами?
4. В чем сущность метода сечений?
5. По каким формулам находят координаты центра тяжести плоской фигуры?
6. Какие оси называются главными?
7. Для каких фигур можно без вычислений установить положение главных центральных осей?
8. Относительно каких центральных осей осевые моменты инерции имеют наибольшее и наименьшее значения?
9. Что такое чистый и поперечный изгиб?
10. Какие внутренние усилия возникают в поперечных сечениях бруса в общем случае действия на него плоской системы сил?
11. Какие правила знаков приняты для каждого из внутренних усилий?
12. Какие уравнения используются для определения значения опорных реакций?
13. Как проверить правильность определения опорных реакций?
14. Что такое эпюра поперечных сил, эпюра продольных сил и эпюра изгибающих моментов? Что представляет собой каждая ордината этих эпюр?
15. Почему при построении эпюр Q и М для балки, заделанной одним концом, можно обойтись без определения опорных реакций?
16. Какие перемещения получают поперечные сечения балок при прямом изгибе?
Дата добавления: 2018-11-26; просмотров: 1388;











