Основные формулы для расчета элементов металлических конструкций по первой группе предельных состояний

Для расчета элементов металлических конструкций при действии статических нагрузок различного вида используют следующие зависимости:

1. Расчет на прочность элементов, подверженных центральному растяжению или сжатию следует выполнять по формуле

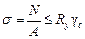, (3.8)

где σ – нормальные напряжения в элементе, МПа;

N – расчетное усилие, действующее в стержне, кН;

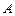– площадь сечения стержня нетто (за вычетом ослаблений сечения стержня, например – отверстиями), м²;

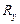– расчетное сопротивление материала, МПа;

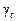– коэффициент условий работы конструкции, характеризующий особенности нагрузки, изменчивости среды и др.

Условие (3.8) позволяет решать три задачи:

– выполнять проверочный расчет – непосредственно по формуле (3.8);

– подбирать требуемое сечение (проектный расчет)

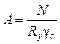; (3.8,а)

– определять предельную силу

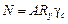. (3.8,б)

2. Расчет на прочность элементов при поперечном изгибе выполняется по зависимостям:

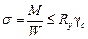; (3.9)

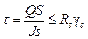, (3.10)

где 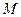, 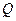– расчетный изгибающий момент и поперечная сила, кН и кН∙м соответственно;

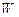– момент сопротивления поперечного сечения элемента, м³;

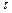– максимальные касательные напряжения в элементе конструкции от расчетных силовых воздействий, МПа;

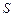– статический момент сдвигающейся части сечения относительно нейтральной оси, м³;

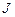– момент инерции сечения относительно нейтральной оси, м⁴;

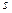– толщина сечения, в котором определяются напряжения, м.

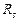– расчетное сопротивление материала при сдвиге, МПа.

3. При проверке на устойчивость центрально-сжатых элементов расчет сплошностенчатых элементов, подверженных центральному сжатию расчетной силой N, выполняется по формуле

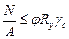, (3.11)

где 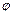– коэффициент продольного изгиба (коэффициент уменьшения расчетного сопротивления сжатию).

Значения j можно вычислить по формулам:

при 0 < 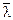£ 2,5

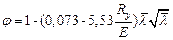; (3.12)

при 2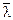,5 < £ 4,5

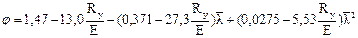; (3.13)

при 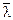> 4,5

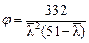. (3.14)

В приведенных формулах 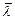– условная гибкость стержня, определяемая через гибкость стержня 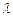(подробнее см. в разделе по расчету колонн) так

,

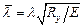здесь 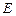– модуль упругости стали (МПа).

Численные значения j для стали приведены в табл. А8 приложения А.

4. При проверке на прочность элементов, работающих на срез (сдвиг), используется формула (3.10)

5. При проверке на прочность элементов, находящихся в сложнонапряженном состоянии, одновременно подверженных действию нормальных 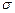и касательных (тангенциальных) 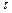напряжений,

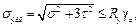(3.15)

где 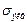– эквивалентное (приведенное) напряжение, МПа.

6. При проверке на прочность оболочек, находящихся в двухосном напряженном состоянии,

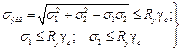, (3.16)

где 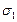и 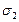– соответственно меридиональные и кольцевые напряжения.

Второе расчетное предельное состояние требует надлежащей жесткости конструкции с тем, чтобы величина относительной деформации не превышала допустимой.

Для элементов, воспринимающих действие осевой силы, это условие состоит в том, чтобы гибкость конструкции не превышала допустимой, т.е.

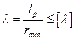, (3.17)

где 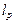– расчетная длина элемента, м;

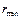– наименьший радиус инерции его сечения, м;

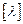– допустимая гибкость элемента (см. таблицу А16).

При определении деформации возможная перегрузка не учитывается, т.е. принимается 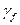= 1.