Методика расчета по предельным состояниям

Согласно СНиП II-23-81* [6] (СНиП – Строительные нормы и правила) для стальных конструкций, при расчете их по этому методу, различают две группы предельных состояний:

1) по потере несущей способности конструкции (из-за пластического, хрупкого, усталостного разрушения и потери устойчивости) или полной непригодности к эксплуатации (из-за текучести материала, неупругого сдвига в соединениях, ползучести и др.);

2) по непригодности к нормальной эксплуатации вследствие появления недопустимых перемещений (прогибов, поворотов или осадок) при статических нагрузках и колебаний при динамических нагрузках.

В общем виде условие работоспособности конструкций и элементов при расчете их по первой группе предельных состояний можно записать следующей формулой:

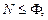(3.1)

где 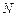– расчетные силовые факторы (продольная сила при растяжении-сжатии, изгибающий момент при изгибе и т.д.), возникающие в сечении элемента от действия одной или совокупности нагрузок в самом опасном их сочетании;

Φ – наименьшая возможная несущая способность элемента конструкции, подвергающегося растяжению, сжатию или изгибу.

Величина 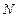может представлять собой расчетную продольную силу 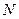(кН), перерезывающую силу 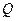(кН) или изгибающий момент 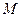(кН∙м), а величина Ф зависит от геометрических размеров сечения, прочностных свойств материала и условий работы конструкции.

С целью выравнивания фактических запасов прочности разнообразных конструкций при расчете их по предельным состояниям вводятся поправочные коэффициенты, учитывающие:

– возможные отклонения нагрузок от нормативных значений (коэффициент надежности по нагрузке );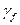

– свойства материала (коэффициент надежности по материалу );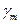

– различные условия работы материалов и конструкций в условиях эксплуатации (коэффициент условий работы );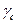

– степень ответственности сооружений (зданий) (коэффициент надежности по назначению (ответственности) ).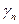

Числовые значения этих коэффициентов (см. приложение 1) и их сочетание для конкретных расчетов устанавливаются в СНиП.

Расчетные нагрузки (сосредоточенные 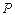, распределенные 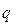и др.) находят из нормативных (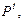 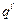) путем умножения их на соответствующие коэффициенты надежности по нагрузке 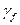(см. табл. А1 приложения А):

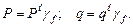(3.2)

Коэффициенты надежности по нагрузке 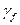для каждого вида нагрузки могут быть различными (см. таблицу А1 приложения А). Они позволяют учесть превышение каждой фактической нагрузки по сравнению с ее нормативным значением.

Нагрузки разделяют на постоянные, временные (временные длительные, кратковременные) и особые [6].

Постоянные нагрузки: вес частей зданий и сооружений, в том числе несущих и ограждающих строительных конструкций; вес и давление грунтов (насыпей, засыпок), горное давление; воздействия предварительного напряжения конструкций.

Длительные нагрузки: вес временных перегородок; стационарного оборудования (станки, аппараты, моторы, емкости и т. д.); давление газов, жидкостей и сыпучих тел в емкостях и трубопроводах в процессе их эксплуатации; нагрузки на перекрытия в складских помещениях и др.

Кратковременные нагрузки: нагрузки от оборудования, возникающие в пускоостановочном, переходном и испытательном режимах, а также при его перестановке или замене; вес людей, ремонтных материалов в зонах обслуживания и ремонта оборудования; снеговые нагрузки; ветровые нагрузки; гололедные нагрузки и др.

Особые нагрузки: сейсмические и взрывные воздействия; нагрузки, вызываемые резкими нарушениями технологического процесса, временной неисправностью или поломкой оборудования и др.

Нагрузки действуют на конструкцию в сочетании друг с другом. При этом одновременное воздействие нескольких нагрузок максимальной интенсивности (например, нагрузок на подкрановую балку от двух сближенных кранов) считается маловероятным, что учитывается умножением их на коэффициенты сочетаний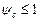

Если обозначить 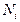часть расчетного усилия от любого произвольного количества расчетных нагрузок 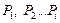, то совокупное расчетное усилие (с учетом формулы 3.2) будет определяться так:

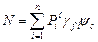, (3.3)

В основу расчета металлических конструкций по методу предельных состояний, положены так называемые нормативные расчетные сопротивления материала (или сварного соединения) 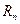, ( 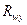). Значения этих величин устанавливаются исходя из механических свойств материала, вида напряженного состояния, а для соединений – в зависимости от типа соединения и способа его получения.

Нормативное сопротивление материала принимается равным пределу текучести 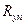или временному сопротивлению 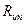в зависимости от условий работы конструкции и свойств материала.

Расчетное сопротивление материала растяжению, сжатию, изгибу по пределу текучести 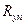или по временному сопротивлению 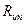находят из соотношений:

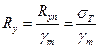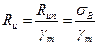; . (3.4)

В этих формулах 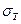и 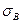– предел текучести и временное сопротивление (предел прочности) стали, определяемые по ГОСТу или ТУ.

Коэффициент надежности по материалу 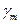позволяет учесть возможные отклонения сопротивлений материалов в неблагоприятную сторону от нормативных значений.

Формулы для определения расчетных сопротивлений проката, гнутых профилей и труб для других видов напряженных состояний (смятие, срез) приведены в таблице А2 приложения А, а коэффициента 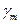– в таблице А3.

Расчетные сопротивления для сварных соединений зависят от типа соединения (стыковое, нахлесточное и т.д.), способа сварки, вида напряженного состояния и выражают в долях от расчетных сопротивлений для основного металла. Формулы для определения расчетных сопротивлений сварных соединений в стальных конструкциях приведены в таблице А4 приложения А.

С учетом изложенного зависимость (3.1) можно преобразовать к следующему виду:

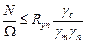, (3.5)

где 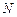– расчетное силовое воздействие (сила, изгибающий момент);

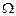– геометрическая характеристика рассчитываемого сечения (площадь поперечного сечения А, момент сопротивления сечения W и т.д.).

Левая часть выражения (3.5) представляет собой максимальное нормальное напряжение ( 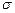), действующее в рассматриваемом сечении.

Если для упрощения в формуле (3.3) принять 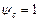, а нагрузки будут действовать одного вида, то тогда 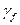= const и, следовательно, выполнение условия работоспособности (3.1) можно преобразовать к виду

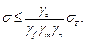(3.6)

Величина 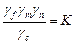является коэффициентом запаса прочности по отношению к пределу текучести материала .

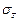Таким образом, при использовании методики расчета конструкции по первой группе предельных состояний не вводят постоянного коэффициента запаса прочности, последний заменен коэффициентами, которые в разных сочетаниях дают различные значения коэффициента запаса.

При расчете металлических конструкций по второй группе предельных состояний (чаще всего по прогибам) должно соблюдаться условие

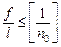, (3.7)

где 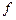– прогиб элемента (например, балки) от действия нагрузки;

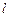– длина элемента (пролет балки);

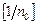– предельный относительный прогиб (таблица А7 приложения А).