Приближенные (итерационные) методы решения НАУ
Постановка задачи
Дано нелинейное алгебраическое уравнение (НАУ) вида
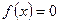 (1.1)
(1.1)
Нелинейность уравнения означает, что аргумент функции 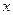 входит в функцию
входит в функцию 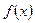 в некоторой степени или под знаком функции (тригонометрической, логарифмической и т.п.), и, следовательно, графиком этой функции не является прямая линия. Решить уравнение – это значит найти такое
в некоторой степени или под знаком функции (тригонометрической, логарифмической и т.п.), и, следовательно, графиком этой функции не является прямая линия. Решить уравнение – это значит найти такое 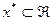 что
что 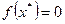 .Значение
.Значение 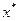 называют корнем уравнения. На графике функции
называют корнем уравнения. На графике функции 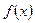 корню соответствует точка, в которой функция пересекает ось абсцисс. Нелинейное уравнение, в общем случае, может иметь несколько корней, как, например, на рис. 1.1 корнями являются точки
корню соответствует точка, в которой функция пересекает ось абсцисс. Нелинейное уравнение, в общем случае, может иметь несколько корней, как, например, на рис. 1.1 корнями являются точки 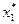 ,
, 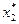 ,
, 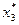 .
.
 Все методы решения нелинейных алгебраических уравнений вида(1.1) можно разделить на два класса. Это точные (аналитические) и приближенные (итерационные) методы. В точных методах корень уравнения находится при помощи некоторой алгебраической формулы. Примерами служат решения квадратных уравнений, некоторых видов тригонометрических, логарифмических, показательных уравнений и т.д., способы решения которых известны нам из школьного курса.
Все методы решения нелинейных алгебраических уравнений вида(1.1) можно разделить на два класса. Это точные (аналитические) и приближенные (итерационные) методы. В точных методах корень уравнения находится при помощи некоторой алгебраической формулы. Примерами служат решения квадратных уравнений, некоторых видов тригонометрических, логарифмических, показательных уравнений и т.д., способы решения которых известны нам из школьного курса.
 На практике часто встречаются функции
На практике часто встречаются функции 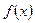 столь сложного вида, что процесс нахождения точного решения либо чрезвычайно затруднен, либо вовсе невозможен. В этом случае приходится прибегать к приближенным методам решения. В приближенных методах процесс нахождения решения (корней уравнения), вообще говоря, бесконечен. В этом случае решение ищется в виде бесконечной последовательности
столь сложного вида, что процесс нахождения точного решения либо чрезвычайно затруднен, либо вовсе невозможен. В этом случае приходится прибегать к приближенным методам решения. В приближенных методах процесс нахождения решения (корней уравнения), вообще говоря, бесконечен. В этом случае решение ищется в виде бесконечной последовательности 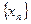 , такой, что
, такой, что 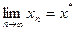 , где
, где 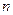 – это индекс, указывающий на номер приближения или итерации. По определению предела,для любого сколь угодно малого
– это индекс, указывающий на номер приближения или итерации. По определению предела,для любого сколь угодно малого 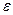 найдется такое N, что при n>N,
найдется такое N, что при n>N, 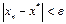 . Члены последовательности
. Члены последовательности 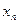 называются последовательными приближениями к решению, или итерациями. Наперед заданное число
называются последовательными приближениями к решению, или итерациями. Наперед заданное число 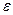 называют точностью метода, а N – это количество итераций, которое необходимо выполнить, чтобы получить решение с точностью
называют точностью метода, а N – это количество итераций, которое необходимо выполнить, чтобы получить решение с точностью 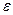 .
.
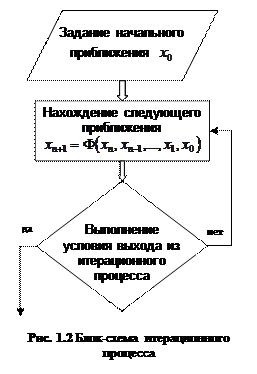
Существует различные методы нахождения приближенного решения, т.е. способы построения последовательности итераций 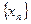 , однако все они имеют общие этапы, представленные на рис. 1.2 в виде блок-схемы.
, однако все они имеют общие этапы, представленные на рис. 1.2 в виде блок-схемы.
Для выхода из итерационного процесса используют различные условия. Наиболее часто используется следующий критерий остановки итерационного процесса: 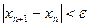 , т.е. процесс нахождения следующего приближения останавливается, когда разница между соседними итерациями становится малой. Также для окончания итерационного процесса используется условие ÷f(xn)÷<e, где f(xn)есть невязка метода.
, т.е. процесс нахождения следующего приближения останавливается, когда разница между соседними итерациями становится малой. Также для окончания итерационного процесса используется условие ÷f(xn)÷<e, где f(xn)есть невязка метода.
Прежде, чем использовать приближенный метод, уравнение необходимо исследовать на наличие корней и уточнить, где эти корни находятся, т.е. найти интервалы изоляции корней. Интервалом изоляции корня называется отрезок, на котором корень уравнения существует и единственный
Необходимое условие существования корня уравнения на отрезке [a,b]: Пусть 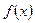 непрерывна и
непрерывна и 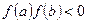 (т.е. на концах интервала функция имеет разные знаки). Тогда внутри отрезка [a, b] существует хотя бы один корень уравнения (1.1).
(т.е. на концах интервала функция имеет разные знаки). Тогда внутри отрезка [a, b] существует хотя бы один корень уравнения (1.1).
Достаточное условие единственности корня на отрезке [a,b]: Корень будет единственным, если 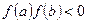 и производная функции
и производная функции 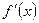 не меняет знак на отрезке [a, b], т.е.
не меняет знак на отрезке [a, b], т.е. 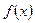 является монотонной на отрезке от
является монотонной на отрезке от 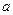 до
до 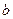 . В этом случае отрезок [a,b] будет интервалом изоляции.
. В этом случае отрезок [a,b] будет интервалом изоляции.
Если уравнение имеет несколько корней, то для каждого из них нужно найти свой интервал изоляции.
Существуют различные способы исследования функции: аналитический, табличный, графический.
Аналитическийспособ состоит в исследовании поведения функции путем нахождении ее экстремумов, исследование ее поведения при 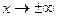 и нахождение участков возрастания и убывания функции.
и нахождение участков возрастания и убывания функции.
Графический способ – это построение графика функции 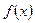 и определение числа корней по количеству пересечений графика с осью
и определение числа корней по количеству пересечений графика с осью 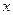 .
.
Табличный способ – это построение таблицы, состоящей из столбца аргумента 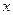 и столбца значений функции
и столбца значений функции 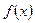 . О наличии корней свидетельствуют перемены знака функции. Чтобы не произошла потеря корней, шаг изменения аргумента должен быть достаточно мелким, а интервал изменения достаточно широким.
. О наличии корней свидетельствуют перемены знака функции. Чтобы не произошла потеря корней, шаг изменения аргумента должен быть достаточно мелким, а интервал изменения достаточно широким.
ПРИМЕР 1.1.Решить нелинейное алгебраическое уравнение 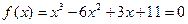 . Исследуем уравнение на интервалы изоляции корней аналитическим способом. Для этого найдем производную функции
. Исследуем уравнение на интервалы изоляции корней аналитическим способом. Для этого найдем производную функции 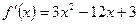 . Далее определим экстремумы функции, где, как известно, производная принимает нулевое значение:
. Далее определим экстремумы функции, где, как известно, производная принимает нулевое значение:
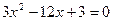
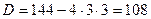
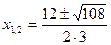 , откуда
, откуда 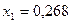 ,
, 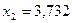 .
.
Значения функции в экстремальных точках: 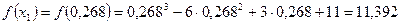
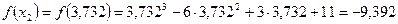 . Так как
. Так как 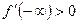 , то
, то 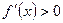 при
при 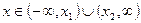 , и
, и 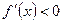 при
при 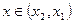 . Кроме того,
. Кроме того, 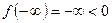 ,
, 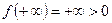 . Следовательно, на интервале
. Следовательно, на интервале 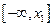 функция возрастает от
функция возрастает от 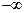 до 11,392; на интервале
до 11,392; на интервале 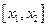 - убывает до -9,392, и на интервале
- убывает до -9,392, и на интервале 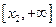 возрастает до
возрастает до 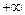 . Т.е. уравнение имеет три корня. Найдем интервалы изоляции для каждого из корней.
. Т.е. уравнение имеет три корня. Найдем интервалы изоляции для каждого из корней.
Рассмотрим для первого корня отрезок 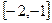 . На левом конце отрезка функция принимает значение
. На левом конце отрезка функция принимает значение 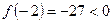 , а на правом
, а на правом 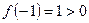 . Так как внутри этого отрезка производная положительна, то функция является монотонно возрастающей, т.е. меняет знак только один раз. Следовательно, отрезок
. Так как внутри этого отрезка производная положительна, то функция является монотонно возрастающей, т.е. меняет знак только один раз. Следовательно, отрезок 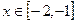 является интервалом изоляции первого корня. Рассмотрим для второго корня отрезок
является интервалом изоляции первого корня. Рассмотрим для второго корня отрезок 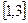 :
: 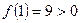 ,
, 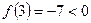 ,
, 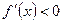 при
при 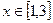 , т.е. этот отрезок является интервалом изоляции второго корня.
, т.е. этот отрезок является интервалом изоляции второго корня.
Рассмотрим для третьего корня отрезок 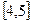 :
: 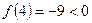 ,
, 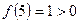 ,
, 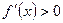 при
при 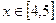 , т.е. этот отрезок является интервалом изоляции третьего корня.
, т.е. этот отрезок является интервалом изоляции третьего корня.
Табличный способ:
В интервале от -5 до 6 с шагом 1 вычислим значения функции. Результаты представим в виде таблицы:
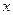
| -5 | -4 | -3 | -2 | -1 | |||||||
| f(x) | -279 | -161 | -79 | -27 | -7 | -9 |
Из таблицы видно, что смена знака функции происходит три раза на интервалах 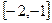 ,
, 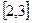 и
и 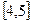 . Эти интервалы и можно выбрать в качестве интервалов изоляции корней.
. Эти интервалы и можно выбрать в качестве интервалов изоляции корней.
Графический способ
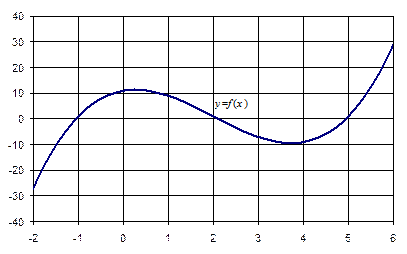
Для нахождения интервалов изоляции графическим способом необходимо построить график функции и выбрать те отрезки, в пределах которых график пересекает ось 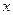 только один раз. На рис. 1.3 представлен построенный в Excel график функции
только один раз. На рис. 1.3 представлен построенный в Excel график функции 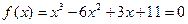 , из которого следует, что интервалы изоляции корней могут быть выбраны следующим образом: [-2, 0], [1, 3] и [4, 6].
, из которого следует, что интервалы изоляции корней могут быть выбраны следующим образом: [-2, 0], [1, 3] и [4, 6].
| |
| Рис. 1.3. Иллюстрация графического способа исследования НАУ |
Приближенные (итерационные) методы решения НАУ
Пусть интервалы изоляции корней известны. Познакомимся с несколькими итерационными методами, позволяющими найти корень на известном интервале изоляции [a, b].
Дата добавления: 2021-09-07; просмотров: 436;











