Метод обратной матрицы
Если 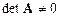 , то существует матрица
, то существует матрица 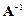 , обратная к данной. Умножим исходную систему уравнений (2.1) на обратную матрицу слева. Получим
, обратная к данной. Умножим исходную систему уравнений (2.1) на обратную матрицу слева. Получим
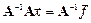 .
.
Известно, что произведение обратной матрицы на исходную дает единичную матрицу 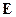 , и, следовательно, получаем
, и, следовательно, получаем 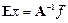 , или
, или
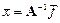 (2.3)
(2.3)
Решение СЛАУ свелось к умножению известной обратной матрицы на вектор правых частей. Таким образом, задача решения СЛАУ и задача нахождения обратной матрицы связаны между собой, поэтому часто решение СЛАУ называют задачей обращения матрицы. Проблемы использования этого метода те же, что и при использовании метода Крамера: нахождение обратной матрицы – трудоемкая операция. Однако для небольших m решение может быть получено с помощью функций Excel.
ПРИМЕР 2.3. С помощью метода обратной матрицы решить систему 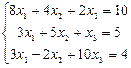
Занесем на рабочий лист Excel матрицу коэффициентов
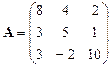 и вектор правых частей
и вектор правых частей 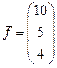 .
.
Выделим на рабочем листе область размером 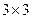 ячейки для обратной матрицы и вызовем функцию МОБР. В поле Массив занесем адреса ячеек исходной матрицы A, и, нажав комбинацию клавиш Ctrl+Shift+Enter, получим A-1:
ячейки для обратной матрицы и вызовем функцию МОБР. В поле Массив занесем адреса ячеек исходной матрицы A, и, нажав комбинацию клавиш Ctrl+Shift+Enter, получим A-1:
| 0.195489 | -0.16541 | -0.02256 |
| -0.1015 | 0.278195 | -0.00752 |
| -0.07895 | 0.105263 | 0.105263 |
Полученную обратную матрицу умножим на вектор правых частей 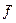 . Для этого выделим столбец из трех ячеек и вызовем функцию МУМНОЖ. В поля Массив 1 и Массив 2 занесем адреса ячеек, в которых находятся найденная обратная матрица и вектор правых частей, после чего, нажав комбинацию клавиш Ctrl+Shift+Enter,получим решение СЛАУ
. Для этого выделим столбец из трех ячеек и вызовем функцию МУМНОЖ. В поля Массив 1 и Массив 2 занесем адреса ячеек, в которых находятся найденная обратная матрица и вектор правых частей, после чего, нажав комбинацию клавиш Ctrl+Shift+Enter,получим решение СЛАУ
| 1.037594 |
| 0.345865 |
| 0.157895 |
Замечание. Если одна из клавиш Ctrlили Shiftне нажата, вычисления будут выполнены не во всем выделенном диапазоне, а только в одной ячейке. В этом случае весь процесс вызова функции необходимо повторить.
Метод Гаусса
Наиболее известным и популярным прямым методом решения СЛАУ является метод Гаусса. Этот метод заключается в последовательном исключении неизвестных. Метод состоит из двух этапов. На первом (прямом) этапе исходная система сводится к системе с треугольной матрицей, которая решается на втором (обратном) этапе. На прямом этапе используются следующие эквивалентные преобразования строк расширенной матрицы системы: перестановка строк, умножение строки на ненулевую константу, сложение строк.
Прямой этап.Пусть в системе уравнений
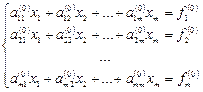
первый элемент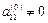 . Назовем его ведущимэлементом первой строки. Разделим все элементы этой строки на
. Назовем его ведущимэлементом первой строки. Разделим все элементы этой строки на 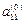 , и исключим
, и исключим 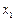 из всех последующих строк, начиная со второй, путем вычитания первой (преобразованной), умноженной на коэффициент при
из всех последующих строк, начиная со второй, путем вычитания первой (преобразованной), умноженной на коэффициент при 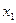 в соответствующей строке. Получим
в соответствующей строке. Получим
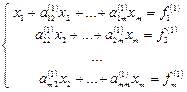 .
.
Если 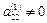 , то на него можно разделить второе уравнение, а затем исключить
, то на него можно разделить второе уравнение, а затем исключить 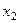 из всех остальных уравнений. С помощью аналогичных преобразований приходим к системе уравнений с верхней треугольной матрицей
из всех остальных уравнений. С помощью аналогичных преобразований приходим к системе уравнений с верхней треугольной матрицей
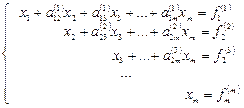 (2.4)
(2.4)
Обратный этап.Решаем систему (2.4) с верхней треугольной матрицей в обратном порядке:
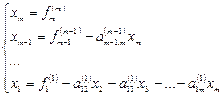 . (2.5)
. (2.5)
В случае если один из ведущих элементов равен нулю, изложенный алгоритм метода Гаусса неприменим. Кроме того, если какие-либо ведущие элементы малы, то это приводит к усилению ошибок округления и ухудшению точности счета. Поэтому обычно используется другой вариант метода Гаусса – схема Гаусса с выбором главного элемента. Путем перестановки строк и других эквивалентных преобразований добиваются выполнения условия: 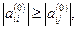
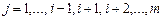 , т.е. осуществляется выбор первого главного элемента. Переставляют уравнения так, чтобы в первом уравнении коэффициент
, т.е. осуществляется выбор первого главного элемента. Переставляют уравнения так, чтобы в первом уравнении коэффициент 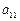 был максимальный по модулю. Разделив первую строку на главный элемент, как и прежде, исключают
был максимальный по модулю. Разделив первую строку на главный элемент, как и прежде, исключают 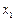 из остальных уравнений. Затем для оставшихся столбцов и строк выбирают второй главный элемент и т.д.
из остальных уравнений. Затем для оставшихся столбцов и строк выбирают второй главный элемент и т.д.
ПРИМЕР 2.4.Рассмотрим применение метода Гаусса с выбором главного элемента на примере следующей системы уравнений:
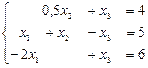 .
.
В первом уравнении коэффициент при 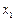 равен 0, во втором 1 и в третьем -2, т.е. максимальный по модулю коэффициент находится в третьем уравнении. Поэтому переставим третье уравнение на место первого:
равен 0, во втором 1 и в третьем -2, т.е. максимальный по модулю коэффициент находится в третьем уравнении. Поэтому переставим третье уравнение на место первого:
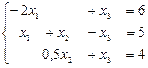 .
.
В третьем уравнении коэффициент при 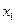 равен 0. Исключим
равен 0. Исключим 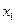 из второго уравнения:
из второго уравнения:
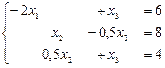
Рассмотрим второе и третье уравнения. Исключим 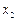 из третьего уравнения. Для этого умножим второе на -0.5 и сложим с третьим:
из третьего уравнения. Для этого умножим второе на -0.5 и сложим с третьим:
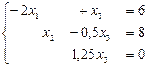 .
.
Далее находим значения 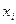 обратным ходом: из третьего уравнения получаем
обратным ходом: из третьего уравнения получаем 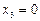 , из второго
, из второго 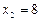 , и из первого
, и из первого 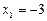 . Выполним проверку:
. Выполним проверку:
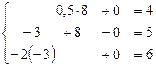 .
.
Такая перестановка уравнений необходима для того, чтобы уменьшить влияние ошибок округления на конечный результат.
Часто возникает необходимость в решении СЛАУ, матрицы которых являютсяслабо заполненными, т.е. содержат много нулевых элементов. В то же время эти матрицы имеют определенную структуру. Среди таких систем выделим системы с матрицами ленточной структуры, в которых ненулевые элементы располагаются на главной диагонали и на нескольких побочных диагоналях. Для решения систем с ленточными матрицами коэффициентов вместо метода Гаусса можно использовать более эффективные методы. Для случая трехдиагональных матриц разработан экономичный метод прогонки.
Метод прогонки
Рассмотрим метод прогонки для СЛАУ вида:
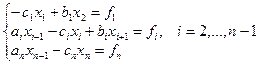 (2.6)
(2.6)
Решение данной системы ищем в виде:
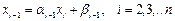 (2.7)
(2.7)
Здесь ai, bi – неизвестные прогоночные коэффициенты. Как и метод Гаусса, метод прогонки состоит из двух этапов. На первом (прямом) этапе определяются прогоночные коэффициенты, на втором (обратном) вычисляется вектор решения.
Прямой этап.Сравнивая соотношение (2.7) при i=2: 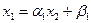 и следствие первого уравнения системы (2.6):
и следствие первого уравнения системы (2.6): 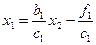 , получим формулы для первых прогоночных коэффициентов:
, получим формулы для первых прогоночных коэффициентов: 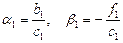 .
.
Подставляя (2.7) во второе уравнение (2.6), получим:
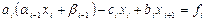 .
.
Или, после преобразования,
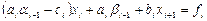 ,
,
откуда
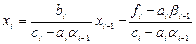
Сравнивая с (2.7), получим
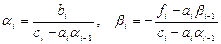 .
.
Таким образом, можно найти все 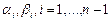 .
.
Обратный этап.Подставляя последнее прогоночное соотношение (2.7) в последнее уравнение (2.6), получим:
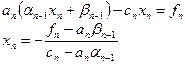 .
.
Затем, последовательно применяя (2.7), находим:
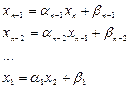 .
.
Таким образом, алгоритм метода прогонки можно представить в виде:
1. Находим 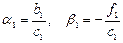 ;
;
2. Для 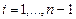 вычисляем
вычисляем
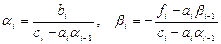 .
.
3. Находим 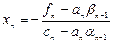 .
.
4. Для 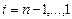 находим:
находим: 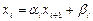 .
.
Теорема. Пусть коэффициенты 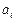 ,
, 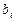 системы уравнений при
системы уравнений при 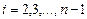 отличны от нуля и пусть
отличны от нуля и пусть 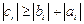 при
при 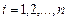 . Тогда прогонка корректна и устойчива.
. Тогда прогонка корректна и устойчива.
При выполнении этих условий знаменатели в алгоритме метода прогонки не обращаются в нуль и, кроме того, погрешность вычислений, внесенная на каком либо шаге расчетов, не будет возрастать при переходе к следующим шагам. Данное условие есть не что иное, как условие диагонального преобладания.
Дата добавления: 2021-09-07; просмотров: 525;











