Метод простой итерации
Для метода простой итерации (МПИ) уравнение (1.1) необходимо сначала преобразовать к виду 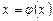 . Это всегда можно сделать с помощью эквивалентных преобразований. Далее, выберем начальное приближение
. Это всегда можно сделать с помощью эквивалентных преобразований. Далее, выберем начальное приближение 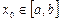 . Следующие итерации производятся по формуле:
. Следующие итерации производятся по формуле: 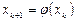 , т.е.
, т.е. 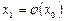 ,
, 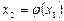 , и т.д. Если последовательность
, и т.д. Если последовательность 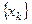 ,
, 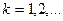 сходится, то
сходится, то 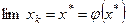 , то есть в пределе получаем искомое решение уравнения. Итерационный процесс следует остановить, когда
, то есть в пределе получаем искомое решение уравнения. Итерационный процесс следует остановить, когда 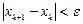 . В качестве начального приближения обычно берут середину отрезка
. В качестве начального приближения обычно берут середину отрезка 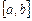 :
: 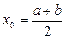 .
.
Привести исходное уравнение (1.1) к виду 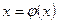 можно бесконечным числом способов. Из всевозможных функций j(x) выбирают ту, которая порождает сходящуюся к корню последовательность
можно бесконечным числом способов. Из всевозможных функций j(x) выбирают ту, которая порождает сходящуюся к корню последовательность 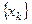 .
.
Достаточное условие сходимости.Пусть 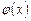 имеет производную на отрезке
имеет производную на отрезке 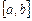 ,
, 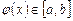 и
и 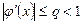 для всех
для всех 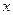 из отрезка
из отрезка 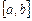 . Тогда итерационный процесс сходится к корню уравнения, т.е.
. Тогда итерационный процесс сходится к корню уравнения, т.е. 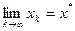 .
.
Доказательство. Из формулы МПИ следует, что
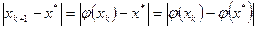
Применяя теорему Лагранжа о среднем, получим
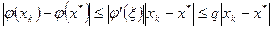 .
.
Аналогично
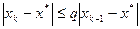 ,
, 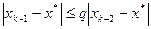 и т.д.
и т.д.
Следовательно,
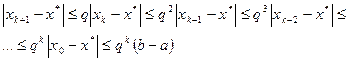
Так как 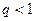 , то
, то 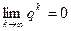 и, следовательно,
и, следовательно, 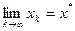 .
.
Геометрическая интерпретация метода простой итерации представлена на рис. 1.4 для случаев 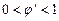 (а),
(а), 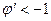 (б),
(б), 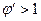 (в) и
(в) и 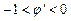 (г).
(г).

| 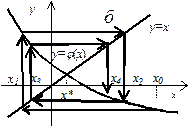
|
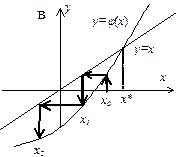
| 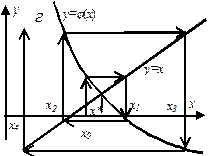
|
| Рис. 1.4.Сходящийся (а, б) и расходящийся (в, г) МПИ |
Метод релаксации
На практике часто в качестве функции 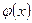 выбирают функцию
выбирают функцию 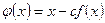 , где
, где 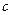 – некоторая постоянная. Постоянную
– некоторая постоянная. Постоянную 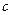 выбирают таким образом, чтобы условие
выбирают таким образом, чтобы условие 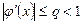 выполнялось бы для всех
выполнялось бы для всех 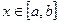 .
.
При таком выборе функции 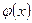 метод простой итерации называют методом релаксации.
метод простой итерации называют методом релаксации.
Получим условия на выбор константы 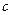 :
:
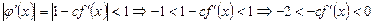
Таким образом, если 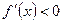 ,то
,то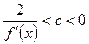 .Если же
.Если же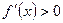 ,то
,то 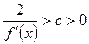 .
.
Отсюда видно, что знак постоянной 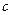 совпадает со знаком производной
совпадает со знаком производной 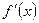 . Часто
. Часто 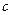 берут в виде:
берут в виде: 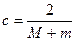 , где
, где 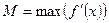 ,
, 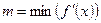 .
.
Убедимся, что такой выбор 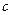 удовлетворяет условию сходимости. Пусть
удовлетворяет условию сходимости. Пусть 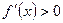 . Тогда
. Тогда 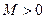 и
и 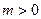 , и, следовательно,
, и, следовательно, 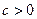 и
и
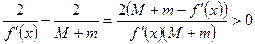 , т.к.
, т.к. 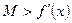 . Следовательно,
. Следовательно, 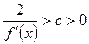 .
.
Пусть теперь 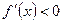 . Тогда
. Тогда 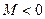 ,
, 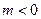
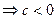 и
и
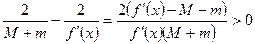 , т.к.
, т.к. 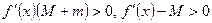 и
и 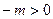 .
.
Следовательно, 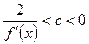 .
.
ПРИМЕР 1.3. Найдем с точностью 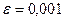 второй корень уравнения
второй корень уравнения 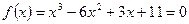 , лежащий на интервале
, лежащий на интервале 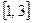 . Для определения значения параметра
. Для определения значения параметра 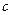 необходимо найти максимальное и минимальное значения производной функции
необходимо найти максимальное и минимальное значения производной функции 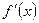 на отрезке
на отрезке 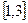 . Для этого необходимо найти значения
. Для этого необходимо найти значения 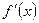 на концах интервала и в точках экстремума, где
на концах интервала и в точках экстремума, где 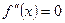 (если эти точки лежат на исследуемом отрезке). Далее среди этих значений выбираютсямаксимальное и минимальное. В нашем случае
(если эти точки лежат на исследуемом отрезке). Далее среди этих значений выбираютсямаксимальное и минимальное. В нашем случае
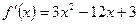 ,
, 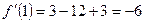
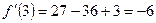 ,
, 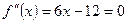 при
при 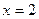
Экстремум производной находится на заданном отрезке 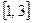 , находим значение производной в этой точке:
, находим значение производной в этой точке: 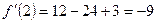 . Следовательно
. Следовательно
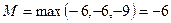 ,
, 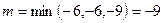 ,
, 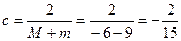 .
.
Таким образом, 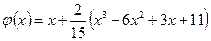 .
.
Выберем начальное приближение 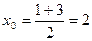 , следующие приближения вычисляются по формуле
, следующие приближения вычисляются по формуле
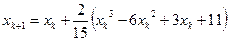 , k=0, 1, 2,..
, k=0, 1, 2,..
Условием окончания итерационного процесса является условие: 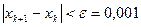 или
или 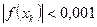 .
.
Результаты вычислений оформим на рабочем листе Excel в виде таблицы:
| A | B | C | |
| Номер итерации | 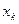
| 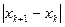
| |
| 2,133333 | 0,133333 | ||
| 2,106983 | 0,026351 | ||
| 2,1121 | 0,005117 | ||
| 2,111101 | 0,000999 | ||
| 2,111296 | 0,000195 |
Здесь формулы для вычисления 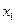 имеют вид: =B2+2/15*(B2^3-6*B2^2+3*B2+11), а для
имеют вид: =B2+2/15*(B2^3-6*B2^2+3*B2+11), а для 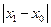 :
:
=ABS(B3-B2). Остальные вычисления получаются простым копированием формул.
Дата добавления: 2021-09-07; просмотров: 450;











