МЕТОДЫ РЕШЕНИЯ СИСТЕМ ЛИНЕЙНЫХ АЛГЕБРАИЧЕСКИХ УРАВНЕНИЙ

К решению систем линейных алгебраических уравнений сводятся многочисленные практические задачи (по некоторым оценкам, более 75% всех задач). Можно с полным основанием утверждать, что решение линейных систем является одной из самых распространенных и важных задач вычислительной математики. Существует много методов и современных пакетов прикладных программ для решения СЛАУ, но для того, чтобы их успешно использовать, необходимо разбираться в основах построения методов и алгоритмов, иметь представления о недостатках и преимуществах используемых методов.

Постановка задачи

Требуется найти решение системы 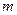линейных уравнений, которая в общем виде записывается в виде

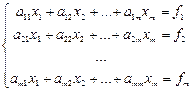. (2.1)

В матричном виде эта система уравнений записывается как:

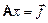(2.1¢)

где 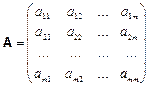- матрица системы, 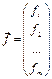- вектор правых частей, 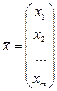- вектор неизвестных.

Таким образом, задача состоит в том, чтобы при известных коэффициентах матрицы 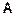и элементах вектора 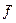найти такие значения 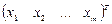, что при подстановке их в систему уравнений (2.1) они превращаются в тождества.

Необходимым и достаточным условием существования единственного решения СЛАУ является условие 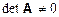, т.е. определитель матрицы 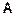не равен нулю. В случае равенства нулю определителя матрица 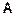называется вырожденной и при этом СЛАУ (2.1) либо не имеет решения, либо имеет их бесчисленное множество. В дальнейшем мы будем предполагать наличие единственного решения.

Все методы решения линейных алгебраических задач можно разбить на два класса: прямые (точные) и итерационные (приближенные).