Энергетические характеристики ядра
Ядро представляет систему связанных между собой нуклонов. Возникновение связанного состояния возможно только под действием ядерных сил притяжения, удерживающих нуклоны в ограниченном объеме. Устойчивость связанного состояния обеспечивается тем, что ядро как система из взаимодействующих между собой нуклонов должна иметь минимум полной энергии. Полная энергия Е1 системы из А нуклонов до объединения в ядро, т.е. находящихся между собой на таких расстояниях, когда действием сил между ними можно пренебречь, будет равна (массы выражены в единицах энергии)
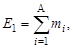
| (1.4.1) |
где mi – массы нуклонов, из которых образовано ядро.
После объединения нуклонов в ядро массой М полная энергия составит
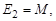
| (1.4.2) |
а изменение энергии системы будет равно
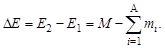
| (1.4.3) |
Работа сил притяжения вызывает переход системы в состояние с меньшей энергией, поэтому величина ΔЕ < 0 будет равна той энергии, которая выделяется при образовании ядра и передается в окружающее пространство преимущественно в виде жесткого электромагнитного излучения. Наоборот, чтобы разрушить ядро и удалить нуклоны на такие расстояния, где их можно считать свободными, потребуется затратить энергию |ΔЕ|. Величина
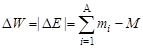
| (1.4.4) |
называется полной энергией связи ядра и справедливо в любой инерциальной системе отсчета, так как определяется через разность энергий покоя. Для устойчивого ядра полная энергия связи положительна и равна той энергии, которую надо затратить, чтобы все составляющие ядро нуклоны развести на расстояния, где между ними прекращается действие ядерных сил.
Ядро, как и любое материальное тело с массой М не равной нулю, имеет замечательную точку, которая называется центром инерции ядра. Система координат, начало которой находится в этой точке, называется системой центра инерции (СЦИ, см.§4.5). В СЦИ полная энергия E системы нуклонов, связанных в ядро массой М, будет минимальной и равной, согласно (1.3.4),
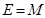 . .
| (1.4.5) |
Полная энергия отдельного нуклона в СЦИ, совершающего движение в пределах ядра, равна сумме массы нуклона mi и его кинетической энергии движения относительно общего центра инерции Тi:
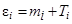 . .
| (1.4.6) |
Полная энергия системы взаимодействующих нуклонов, помимо энергии покоя отдельных нуклонов и их кинетической энергии, включает и энергию взаимодействия нуклонов друг с другом:
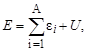
| (1.4.7) |
где через U обозначена суммарная потенциальная энергия нуклонов в ядре. Из трех последних формул получаем
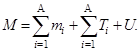
| (1.4.8) |
Из определения энергии связи (1.4.4) и формулы (1.4.8) имеем
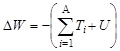 . .
| (1.4.9) |
Сила взаимодействия Fi отдельного нуклона, находящегося вне ядра, с полем центральных сил, создаваемых остальными нуклонами, и его потенциальная энергия Ui в этом поле связаны соотношением:
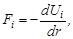
| (1.4.10) |
 где r – расстояние нуклона от центра инерции ядра. Поскольку на такой нуклон со стороны ядра действует сила притяжения, то проекция вектора силы на ось r будет отрицательна. Так как при r → ∞ потенциальная энергия нуклона Ui → 0, а величина dUi/dr в (1.4.10) должна быть больше нуля,то из этого следует, что Ui < 0 (см. рис.1.4.1), т.е. нуклон находится в потенциальной яме. В точке R нуклон захватывается поверхностным слоем ядра, и его потенциальная энергия внутри ядра не меняется. Следовательно, внутри ядра на нуклон не действуют ядерные силы, а на поверхности ядра возникает потенциальный барьер, который препятствует вылету из ядра отдельных или группы связанных нуклонов. Суммарная потенциальная энергия U всех нуклонов будет, очевидно, так же отрицательна. Таким образом, если в (1.4.9) U < 0, а |U| >
где r – расстояние нуклона от центра инерции ядра. Поскольку на такой нуклон со стороны ядра действует сила притяжения, то проекция вектора силы на ось r будет отрицательна. Так как при r → ∞ потенциальная энергия нуклона Ui → 0, а величина dUi/dr в (1.4.10) должна быть больше нуля,то из этого следует, что Ui < 0 (см. рис.1.4.1), т.е. нуклон находится в потенциальной яме. В точке R нуклон захватывается поверхностным слоем ядра, и его потенциальная энергия внутри ядра не меняется. Следовательно, внутри ядра на нуклон не действуют ядерные силы, а на поверхности ядра возникает потенциальный барьер, который препятствует вылету из ядра отдельных или группы связанных нуклонов. Суммарная потенциальная энергия U всех нуклонов будет, очевидно, так же отрицательна. Таким образом, если в (1.4.9) U < 0, а |U| > 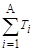 , то DW > 0 и ядро устойчиво. Если же |U| <
, то DW > 0 и ядро устойчиво. Если же |U| < 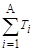 , то DW < 0 и нуклоны ядра будут разлетаться подобно свободным частицам.
, то DW < 0 и нуклоны ядра будут разлетаться подобно свободным частицам.
Следовательно, масса ядра и его устойчивость определяются тем, насколько величина энергии притяжения между нуклонами превышает суммарную кинетическую энергией движения нуклонов в ядре.
Выражая массу протона и нейтрона в энергетических единицах, применим определение (1.4.4) к ядру (A,Z):
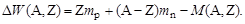
| (1.4.11) |
Эта же величина, выраженная в массовых единицах, называется дефектом массы ядра. Следует отметить принципиальное различие между понятиями декремента массы нуклида (1.3.3) и дефектом массы ядра. Например, для атома 12С декремент массы равен нулю по определению, а дефект массы ядра составляет 0,098940 а.е.м., или 92,1626 МэВ.
Формула (1.4.11) используется при теоретическом исследовании энергетических характеристик ядер, но неудобна для выполнения численных расчетов, поскольку, как отмечено выше, экспериментально измеряемой величиной является масса нуклида Mат(A,Z), которая обычно приводится в справочных таблицах. Прибавляя к правой части выражения (1.4.11) и вычитая Z·me, получим энергию связи ядра
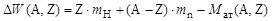
| (1.4.12) |
с точностью до энергии связи атомных электронов с ядром (см. (1.3.5)). В случае атомных масс выражение (1.4.12) будет иметь вид:
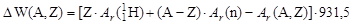 , ,
| (1.4.13) |
если энергию связи выражать в единицах МэВ. Выразим в (1.4.13) атомные массы через декременты масс, используя (1.3.3):
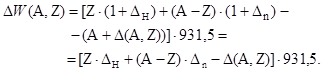
| (1.4.14) |
Последнее выражение показывает, что полная энергия связи ядра обусловлена относительными величинами, значения которых много меньше единицы, и как важно понятия декремента масс нуклида в ядерной физике. В настоящее время эта важнейшая характеристика определена из прецизионных масс-спектрометрических измерений атомных масс практически для всех известных нуклидов.
Величина DW меняется от единиц и десятков МэВ для легких ядер и более чем 1 ГэВ - для тяжелых:
| Ядро | DW (МэВ) | Ядро | DW (МэВ) |
| 2H 12C 16O | 2,2 92,2 127,6 | 131Xe 208Pb 238U | 1103,5 1636,5 1801,7 |
и увеличиваясь с ростом числа нуклонов в ядре не дает представления об интенсивности связи отдельного нуклона в ядре. Для этой цели больше подходит удельная (или средняя) энергия связи 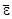 ядра нуклида (A,Z), т.е. полная энергия связи, отнесенная к одному нуклону:
ядра нуклида (A,Z), т.е. полная энергия связи, отнесенная к одному нуклону:
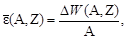
| (1.4.15) |
которая служит мерой прочности ядра
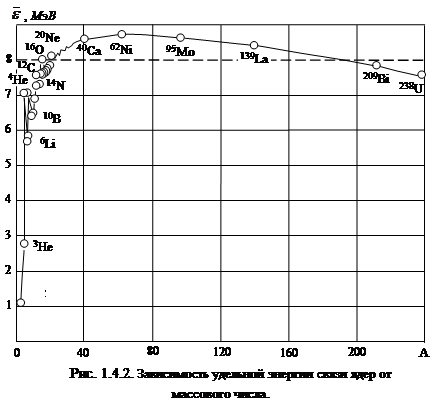
На рис.1.4.2 показана зависимость удельной энергии связи 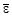 от массового числа А, рассчитанная по формуле (1.4.15) для ядер изобаров, лежащих на дорожке стабильности. Анализ хода кривой
от массового числа А, рассчитанная по формуле (1.4.15) для ядер изобаров, лежащих на дорожке стабильности. Анализ хода кривой 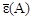 позволяет установить некоторые особенности взаимодействия между нуклонами в ядре.
позволяет установить некоторые особенности взаимодействия между нуклонами в ядре.
1. Удельная энергия связи 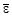 ядра быстро возрастает при малых А, и уже для ядер с А > 12 имеет примерно постоянное значение, близкое к 8 МэВ/нуклон, т.е. ΔW ≈
ядра быстро возрастает при малых А, и уже для ядер с А > 12 имеет примерно постоянное значение, близкое к 8 МэВ/нуклон, т.е. ΔW ≈ 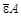 Приближенная независимость
Приближенная независимость 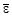 от А свидетельствует о свойстве насыщения ядерных сил, которое выражается в том, что каждый нуклон в ядре может взаимодействовать только с ограниченным числом (очевидно соседних) нуклонов и с ростом числа возможных партнеров по взаимодействию перестает «замечать» остальных. Другими словами, у каждого нуклона имеется ограниченное число возможных связей. Свойство насыщения тесно связано с короткодействием ядерных сил (§1.9 п.2) и указывает на то, что ядерные силы имеют радиус действия порядка среднего
от А свидетельствует о свойстве насыщения ядерных сил, которое выражается в том, что каждый нуклон в ядре может взаимодействовать только с ограниченным числом (очевидно соседних) нуклонов и с ростом числа возможных партнеров по взаимодействию перестает «замечать» остальных. Другими словами, у каждого нуклона имеется ограниченное число возможных связей. Свойство насыщения тесно связано с короткодействием ядерных сил (§1.9 п.2) и указывает на то, что ядерные силы имеют радиус действия порядка среднего
 |
расстояния между нуклонами в ядре.
При отсутствии насыщения каждый из А нуклонов в ядре мог бы взаимодействовать со всеми остальными нуклонами (как это имеет место для кулоновского или гравитационного взаимодействия), и вместо линейной зависимости ΔW ≈ 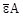 , была бы зависимость
, была бы зависимость
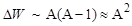 , ,
| (1.4.16) |
так как каждый их нуклонов в этом случае мог бы взаимодействовать со всеми оставшимися (А–1) нуклонами, а всего таких пар А/2.
Насыщение ядерных сил препятствует стягиванию ядра при накоплении числа нуклонов, и объемы ядер оказываются пропорциональными числу нуклонов в ядре, что свидетельствует о приблизительно постоянной плотности ядерного вещества.
2. Максимум удельной энергии связи приходится на ядра с массовыми числами 55 ÷ 60 и спадает к обоим краям кривой.
3. Резкое уменьшение 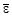 (А) в области малых А можно объяснить тем, что для малого числа взаимодействующих нуклонов насыщения ядерных сил не достигается, и согласно (1.4.16) в этой области
(А) в области малых А можно объяснить тем, что для малого числа взаимодействующих нуклонов насыщения ядерных сил не достигается, и согласно (1.4.16) в этой области 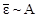 . Последовательное увеличение числа нуклонов в ядре приводит к росту насыщения ядерных сил и примерно постоянному значению
. Последовательное увеличение числа нуклонов в ядре приводит к росту насыщения ядерных сил и примерно постоянному значению 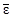 .
.
На этом участке кривой 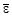 (А) наблюдаются резкие «пики», отвечающие ядрам 4H, 12C, 16O, которые указывают на кластерную структуру этих ядер. Для этих ядер энергетически выгодным оказывается объединение нуклонов в α-частичные кластеры (2p+2n).
(А) наблюдаются резкие «пики», отвечающие ядрам 4H, 12C, 16O, которые указывают на кластерную структуру этих ядер. Для этих ядер энергетически выгодным оказывается объединение нуклонов в α-частичные кластеры (2p+2n).
4. Справа от максимума величина 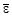 плавно уменьшается, достигая для самого тяжелого природного элемента - урана значения 7,57 МэВ/нуклон. Это уменьшение объясняется электрическим отталкиванием протонов. Поскольку кулоновские силы не обладают свойством насыщения, то при переходе к тяжелым ядрам удельная энергия связи убывает из-за роста электростатической энергии взаимного отталкивания протонов, величина которой пропорциональна Z2. В ядрах с малым числом протонов она незначительна, но существенно влияет на прочность ядер в области тяжелых ядер.
плавно уменьшается, достигая для самого тяжелого природного элемента - урана значения 7,57 МэВ/нуклон. Это уменьшение объясняется электрическим отталкиванием протонов. Поскольку кулоновские силы не обладают свойством насыщения, то при переходе к тяжелым ядрам удельная энергия связи убывает из-за роста электростатической энергии взаимного отталкивания протонов, величина которой пропорциональна Z2. В ядрах с малым числом протонов она незначительна, но существенно влияет на прочность ядер в области тяжелых ядер.
5. Из наличия максимума у зависимости 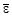 (А) следует важный вывод о двух энергетически выгодных процессах: 1) для наиболее тяжелых ядер возможен процесс деления на два более легких; 2) нескольким легчайшим ядрам, наоборот, энергетически выгодно сливаться друг с другом в более тяжелые ядра (синтез ядер). Оба процесса протекают с выделением большого количества энергии в форме кинетической энергии образующихся продуктов.
(А) следует важный вывод о двух энергетически выгодных процессах: 1) для наиболее тяжелых ядер возможен процесс деления на два более легких; 2) нескольким легчайшим ядрам, наоборот, энергетически выгодно сливаться друг с другом в более тяжелые ядра (синтез ядер). Оба процесса протекают с выделением большого количества энергии в форме кинетической энергии образующихся продуктов.
6. Энергия связи одного присоединяемого или отделяемого от ядра нуклона зависит от четности числа имеющихся в составе ядра протонов и нейтронов. Детальный анализ удельной энергии связи как функции А и Z позволил сделать заключение о наибольшей устойчивости ядер с четным числом протонов и нейтронов (т.н. четно-четных ядер). Эти ядра имеют удельную энергию связи, примерно на 1 МэВ большую, чем соседние ядра, у которых либо N, либо Z - нечетные (Ч‑Н и Н-Ч ядра) и, как отмечалось в п.7 §1.1, имеют наибольшую распространенность в природе. Этот факт свидетельствует о том, что объединение внутри ядра одноименных нуклонов в пары (эффект спаривания) обусловлен действием между ними добавочным ядерных сил и является энергетически выгодным процессом, увеличивающим удельную энергию связи приблизительно на 1 МэВ. Четность числа протонов является определяющей в числе стабильных изотопов. Элементы с четным Z имеют наибольшее число стабильных изотопов, а элементы с нечетным Z имеют не более двух стабильных изотопов. Элементы с Z = 43 и 61 вообще не имеют стабильных изотопов. Также обстоит дело и со стабильными изотонами с четным и нечетным N. Наименьшие значение удельной энергии связи и количества стабильных нуклидов (четыре) имеют нечетно-нечетные ядра. Промежуточное положение по величине удельной энергии связи и распространенности в природе занимают четно-нечетные и нечетно-четные ядра, количества которых равны.
Заслуживает внимания особо высокие значения удельной энергии связи (см. рис. 1.4.2) даже на фоне четно-четных ядер, для ядер с содержанием нейтронов и (или) протонов, равным 2, 8, 20, 28, 50, 82, 126 (только для нейтронов). Эти числа (и соответствующие ядра) получили название магических. Особенно устойчивыми являются дважды магические ядра, у которых и число нейтронов, и число протонов равно одному из магических чисел, например, 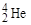 ,
, 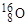 ,
, 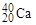 ,
, 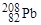 . На рис. 1.4.2 отчетливо видно, что удельная энергия связи для ядер
. На рис. 1.4.2 отчетливо видно, что удельная энергия связи для ядер 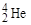 и
и 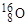 существенно выше соседних.
существенно выше соседних.
Элементы с магическими ядрами имеют большую распространенность в природе. Например, олово, атомный номер которого Z = 50, имеет 10 стабильных изотопов. Наблюдается наибольшее число стабильных изотонов у которых N = 82.
Полезно сравнить удельную энергию ядра с энергией химической связи, выделяющейся в химических реакциях, которая составляет 2 ÷ 5 эВ/молекулу. Поэтому при образовании ядер из нуклонов на единицу массы выделяется энергии в миллионы раз больше, чем при химических реакциях, что, в конечном итоге, определяет практическое значение использования ядерных реакций в качестве источника энергии.
Общее правило (1.4.4) дает возможность рассчитать энергию отделения (энергию связи) любого из нуклонов или группы связанных нуклонов.
Например, энергия отделения нейтрона равна:
 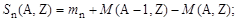
| (1.4.17) |
для протона:
 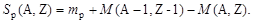
| (1.4.18) |
Эти величины положительны для всех ядер, не испытывающих радиоактивного распада с испусканием отдельных нуклонов (нуклоностабильные ядра), а равенствоихнулю дает границы области существования таких ядер, обозначенные приближенно на рис. 1.1.2. Как следует из (1.4.4), (1.4.17) и (1.4.18) величины 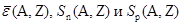 не равны друг другу.
не равны друг другу.
Например, энергия связи a-частицы в ядре урана 238U отрицательна:
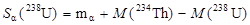 = - 4,2 МэВ, = - 4,2 МэВ,
| (1.4.19) |
что свидетельствует о нестабильность ядра урана относительно a-распада.
 §1.5. Размер ядра
§1.5. Размер ядра
 Первые представления о размерах ядра были получены Резерфордом при экспериментальном изучении рассеяния α-частиц с энергией ~ 5 МэВ при прохождении через тонкие пленки золота. Наблюдалось, что некоторое количество α-частиц рассеивается на очень большие углы θ, почти до 180º. На этом основании в 1911 г. Резерфорд пришел к выводу, что в центре атома (точка о на рис. 1.5.1) имеется область положительного электрического заряда, связанная с большой массой, сконцентрированной в очень малом объеме (по сравнению с объемом атома). На основании закона Кулона для точечных зарядов можно вычислить наименьшее расстояние rmin, на которое может подойти к центру ядра α-частица, летящая точно по направлению к ядру (прицельный параметр b = 0). Для этого следует приравнять ее начальную кинетическую энергию к потенциальной энергии взаимодействия α-частицы с ядром в момент ее полной остановки (в точке поворота):
Первые представления о размерах ядра были получены Резерфордом при экспериментальном изучении рассеяния α-частиц с энергией ~ 5 МэВ при прохождении через тонкие пленки золота. Наблюдалось, что некоторое количество α-частиц рассеивается на очень большие углы θ, почти до 180º. На этом основании в 1911 г. Резерфорд пришел к выводу, что в центре атома (точка о на рис. 1.5.1) имеется область положительного электрического заряда, связанная с большой массой, сконцентрированной в очень малом объеме (по сравнению с объемом атома). На основании закона Кулона для точечных зарядов можно вычислить наименьшее расстояние rmin, на которое может подойти к центру ядра α-частица, летящая точно по направлению к ядру (прицельный параметр b = 0). Для этого следует приравнять ее начальную кинетическую энергию к потенциальной энергии взаимодействия α-частицы с ядром в момент ее полной остановки (в точке поворота):
 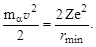
| (1.5.1) |
Формула (1.5.1) верна в предположении неподвижного ядра, когда масса ядра М(A,Z) >> mα – массы α-частицы. Приняв кинетическую энергию α-частицы равной 5 МэВ и положив Z = 79 (золото), получим rmin = 4,5·10-12 см. Естественным было принять эту величину за верхнюю оценку радиуса ядра золота.
Однако необходимо быть уверенным в том, что отбрасываемая в обратном направлении α-частица не проникает в область положительного заряда атома, поскольку равенство (1.5.1) справедливо либо для точечных, либо для сферически симметричных не перекрывающихся зарядов конечных размеров. Тщательная проверка этого предположения была выполнена сотрудниками Резерфорда в 1913 г. и было установлено хорошее согласие экспериментальных результатов рассеяния α-частиц с расчетами по формуле (1.2.2), полученной теоретически на основе закона Кулона. Оказалось, что закон Кулона имеет место для rmin > 3·10-12 см. Подобные эксперименты, выполненные двадцатью годами позже с α-частицами, имеющими энергию в десять и выше МэВ (получены на ускорителях), показали, что когда расстояние между взаимодействующими частицами уменьшается до 10-12 см, наблюдаются резкие отклонения от закона Кулона, а на расстояниях, меньших 10-12 см, обнаруживается действие быстро убывающих с расстоянием сил притяжения, которые перекрывают действие кулоновских сил отталкивания.
В дальнейшем размеры ядер определялись разными способами. Говоря о размерах ядра, нужно всегда иметь в виду, что это достаточно условная величина. Ядро, как квантовомеханическая система, не имеет определенной границы. Наиболее точными считаются оценки размеров ядра по результатам рассеяния ядрами быстрых нейтронов и электронов. Все опыты подтвердили предположения о приблизительно сферической форме ядра, радиус которого определяется через массовое число А как
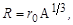
| (1.5.2) |
где r0 = (1,2 ÷ 1,4)·10-13 см.
В опытах по рассеянию быстрых нейтронов на ядрах определяется не радиус ядра, а несколько большее значение радиуса области ядерного взаимодействия, поэтому r0 = (1,3 ÷ 1,4)·10-13 см.
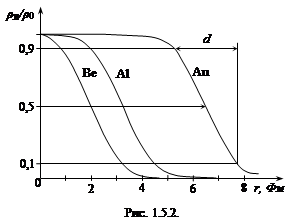 При зондировании ядра быстрыми электронами (опыты Хофштадтера) определяется сфера радиуса R, в которой находятся протоны. Поэтому получают несколько меньшее значение r0 = (1,2 ÷ 1,3)·10-13 см. Высокая точность современных методов исследования с помощью рассеяния быстрых электронов с кинетической энергией Те > 500 МэВ позволяет оценить не только размер области, занятой протонами, но и распределение плотности ρэ электрического заряда по ядру. Поскольку нет причин стабильному ядру иметь различное распределение плотности протонов и нейтронов, то полученные результаты для протонов представляют по существу распределение плотности ρя ядерного вещества в ядре. Распределение ядерного вещества хорошо согласуется с формулой (модель Ферми)
При зондировании ядра быстрыми электронами (опыты Хофштадтера) определяется сфера радиуса R, в которой находятся протоны. Поэтому получают несколько меньшее значение r0 = (1,2 ÷ 1,3)·10-13 см. Высокая точность современных методов исследования с помощью рассеяния быстрых электронов с кинетической энергией Те > 500 МэВ позволяет оценить не только размер области, занятой протонами, но и распределение плотности ρэ электрического заряда по ядру. Поскольку нет причин стабильному ядру иметь различное распределение плотности протонов и нейтронов, то полученные результаты для протонов представляют по существу распределение плотности ρя ядерного вещества в ядре. Распределение ядерного вещества хорошо согласуется с формулой (модель Ферми)
 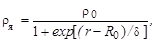
| (1.5.3) |
где R0 = 1,08·10-13·А1/3 см– расстояние от центра ядра до места, где плотность ядра падает вдвое, а δ ≈ 0,55·10 –13 см – определяет скорость убывания плотности ядерного вещества. Спад плотности ядерного вещества от 0,9ρ0 до 0,1ρ0 для всех ядер происходит в пределах одинаковых расстояниях d = 4,4δ= 2,4·10-13 см. Поэтому у легких ядер отсутствует область, где плотность ядерного вещества примерно постоянна (см. рис. 1.5.2).
Дата добавления: 2021-07-22; просмотров: 560;











