Атомное ядро. История открытия ядра.

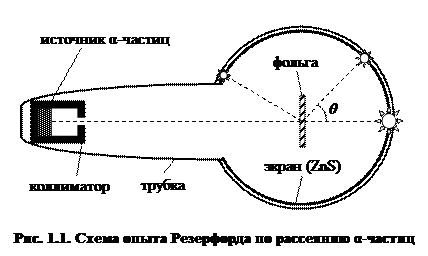
В 1909 г. сотрудники Резерфорда Г. Гейгер и Э. Марсден изучали характер рассеяния α-частиц при прохождении через различные вещества. Опыты, которые поручил им выполнить Резерфорд, заключались в следующем. Внутри вакуумированной стеклянной трубки пропущенный через узкую щель (коллиматор) пучок α-частиц с одинаковой энергией[1] направлялся на экран из сульфида цинка (рис. 1.1). Попадание каждой отдельной α-частицы вызывало на экране световую вспышку (сцинтилляцию), которую можно было наблюдать в лупу или микроскоп. При хорошем вакууме в трубке на экране появлялось яркое пятно от пучка α-частиц. Если на пути пучка помещали тонкую пластинку какого-нибудь вещества, α-частицы распределялись по большой площади экрана. Это распределение и следовало измерить путем подсчета числа частиц, рассеянных на определенный угол.

В процессе измерений Гейгер и Марсден обнаружили неожиданное явление, оказавшееся для Резерфорда весьма существенным. А именно, при прохождении через тонкие (не более 1 мкм) золотые фольги в одном случае из нескольких тысяч рассеянные α-частицы отклонялись на угол более 90^о.

Резерфорд отметил, что распределение рассеянных α-частиц не согласуется с утвердившейся в то время моделью Кельвина-Томсона. Напомним, что последняя трактовала атом как электрически нейтральную сферу размером ~10^-10 м с равномерным распределением положительного заряда, который уравновешивается отрицательным зарядом электронов. Одно из основных положений этой модели было установлено прямым опытом: наличие свободных электронов наблюдалось при разряде в газах. В ее пользу говорило и явление термоэлектронной эмиссии (металлы при нагревании испускают электроны). Наконец, радиоактивные атомы сами по себе способны испускать электроны (β-частицы). Однако присутствие в радиоактивных атомах α-частиц – фрагментов с положительным зарядом – было той загадкой, которую Резерфорд давно стремился разрешить.

Проанализировав результаты опытов Гейгера и Марсдена, Резерфорд пришел к выводу, что рассеяние на большие углы встречается чаще, чем это можно было объяснить взаимодействием со слабым электрическим полем атома Кельвина-Томсона. Действительно, для этого положительный заряд должен быть сконцентрирован в очень малом объеме и при этом связан с большой массой, так как направить частицу обратно может лишь более тяжелый объект (так отражается мяч от стены). Силы, действующие на α-частицу со стороны легких электронов, также слишком малы, чтобы резко изменить ее траекторию.

Вначале кажущееся противоречие пытались истолковать как результат ряда последовательных соударений α-частиц с атомами, т.е. многократным рассеянием. Однако Резерфорд с помощью простых статистических оценок показал, что вероятность рассеяния на большие углы в результате многократного рассеяния на порядок меньше экспериментально наблюдаемой.

На основании вышеперечисленных выводов в 1911 г. Резерфорд предложил «планетарную» модель атома с положительно заряженным ядром малого размера, в котором сосредоточена почти вся масса атома. Электроны располагаются вокруг ядра по сфере радиуса порядка атомного размера, причем количество электронов таково, что их суммарный отрицательный заряд компенсирует положительный заряд ядра Zе. Согласно Резерфорду, наблюдаемое отклонение α-частиц на большие углы является результатом их однократного рассеяния в сильном кулоновском поле ядра. Энергия электростатического взаимодействия между α-частицей и ядром, если рассматривать последние как точечные объекты, равна[2]

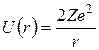, (1.1)

(2е – заряд α-частицы, r – расстояние). Используя эти представления и законы классической механики, а также дополнительное упрощающее предположение (а именно: ядро является настолько тяжелым, что при столкновении может рассматриваться покоящимся), Резерфорд вывел свою знаменитую формулу, определяющую вероятность dN/N рассеяния α-частицы на угол θ (рис. 1.1):

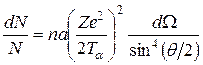, (1.2)

где n – число атомов рассеивающего вещества в единице объема, а – толщина фольги, Т_α – кинетическая энергия α-частицы, dΩ – телесный угол, в пределах которого заключены направления, соответствующие углам рассеяния от θ до θ+dθ (см. ПРИЛОЖЕНИЕ А).

К 1913 г. Гейгер и Марсден произвели проверку формулы Резерфорда путем подсчета сцинтилляций, наблюдавшихся под разными углами рассеяния за одинаковые промежутки времени. В условиях опыта счету подвергались α-частицы, заключенные в пределах одного и того же телесного угла, поэтому число сцинтилляций, наблюдавшихся под разными углами, должно было быть, в соответствии с формулой Резерфорда, пропорционально sin^–4(θ/2). Этот результат теории хорошо подтвердился на опыте. Зависимость рассеяния от толщины фольги и энергии α-частиц также оказалась в соответствии с формулой (1.2).

Теория Резерфорда и выведенная им формула полностью выдержали испытания временем. Это объясняется правильным представлением о структуре материи, на основе которой они были получены. Однако планетарная модель атома породила новые проблемы. Как известно, любая равновесная конфигурация покоящихся точечных электрических зарядов в отсутствие других действующих сил, кроме кулоновских, неустойчива (теорема Ирншоу). Таким образом, в атоме, являющемся устойчивой системой, электроны должны двигаться. С другой стороны, вращающийся вокруг ядра электрон непрерывно должен излучать электромагнитные волны. Теряя энергию на излучение, электрон непрерывно приближался бы к ядру и, в конце концов, упал бы на него. Таким образом, и в этом случае атом оказывается неустойчивым... Понадобилось еще полтора десятилетия, чтобы окончательно убедиться, что классическая механика и электродинамика просто не в состоянии объяснить существование атомов как устойчивых систем, построенных из ядер и электронов. Решение этой проблемы было получено только в рамках квантовой механики.

1.2. Заряд ядра и атомный номер.Экспериментальное подтверждение зависимостей, предсказываемых формулой (1.2), привело к всеобщему признанию предложенной Резерфордом ядерной модели атома. Кроме того, установленный закон рассеяния сделал возможным определение величины зарядов атомных ядер, т.к., согласно формуле Резерфорда, интенсивность рассеяния под данным углом θ пропорциональна квадрату заряда. Именно в результате анализа опытов по рассеянию α-частиц в простых веществах были впервые определены заряды ядер целого ряда элементов (от углерода до платины). Было найдено, что заряд ядра, выраженный в единицах заряда электрона e, равен атомному номеру Z, т.е. порядковому номеру элемента в таблице Д.И. Менделеева. Это соответствие независимым путем было подтверждено в 1913 г. английским физиком Генри Мозли, который предложил метод определения зарядов ядер, основанный на изучении рентгеновских спектров.К тому времени уже было известно, что существует два типа рентгеновского излучения. При небольших энергиях электронов, бомбардирующих антикатод рентгеновской трубки (рис. 1.2), наблюдается лишь тормозное излучение, имеющее сплошной спектр и не зависящее от материала антикатода. Когда же энергия бомбардирующих электронов становится достаточной для выбивания электронов из внутренних оболочек атомов, на фоне тормозного излучения появляются резкие линии характеристического излучения. Оно испускается при переходе электронов с верхних уровней (слоев) на нижние. Длины волн этих линий зависят от природы вещества, из которого изготовлен антикатод.

Линии в рентгеновских спектрах собраны в несколько групп, или серий. Самая коротковолновая (высокочастотная) называется К-серией.Она связана с переходами электронов, заполняющих вакансию в К-слое. Следующая в сторону длинных волн называется L-серией; далее идут серии M и N, наблюдаемые только у тяжелых элементов. Каждая серия насчитывает несколько линий, обозначаемых в порядке уменьшения длины волны индексами α, β, γ, и т.д. Серия K обязательно сопровождается остальными сериями, т. к. при переходе электронов на К-слой образуются вакансии в слоях L, M и т.д., которые будут, в свою очередь, заполнятся электронами из более высоких слоев.

Мозли установил закон, связывающий длины волн рентгеновского спектра λ с атомным номером Z испускающего их элемента:

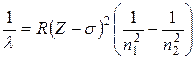, (1.3)

в которой R – постоянная Ридберга, σ – некоторое число, постоянное для каждой серии, n₁ и n₂ – натуральные числа (n₁ < n₂). Например, для линии К_α

.

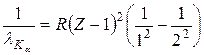Из (1.3) непосредственно следует, что частота любой линии рентгеновского спектра связана с порядковым номером элемента простым соотношением

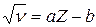, (1.4)

где a и b – постоянные. Соотношения (1.3) и (1.4) позволяют по длине волны (частоте) установить атомный номер элемента и, следовательно – заряд его ядра.

Значение закона Мозли для своего времени было исключительно велико, если принять во внимание, что расположение элементов в периодической системе, основанное на атомных весах[3] и химических свойствах, далеко не во всех случаях было сделано с полной уверенностью. В периодической таблице еще оставались пустые места, отвечающие неоткрытым элементам. Правильность расположения по порядку редкоземельных элементов, химические свойства которых различаются мало, а атомные веса были определены не вполне достоверно, также вызывала сомнения. Закон Мозли устранил все эти затруднения. Он показал со всей определенностью, что от водорода до урана насчитывается 92 химических элемента, тем самым точно указав число еще не открытых элементов. Кроме того, он устранил всякие сомнения в правильности размещения тех элементов, которые были расположены Менделеевым в порядке, противоречащем значениям их атомных весов (Ar–K, Co–Ni, Te–I). Наконец, закон Мозли впервые показал, что не атомный вес, но атомный номер, то есть заряд ядра, определяет химическую индивидуальность атома. Этот вывод нашел подтверждение в открытии изотопов.

1.3. Масса ядра и массовое число. Изотопы.Ядро атома водорода – протон (p) – простейшее ядро. Его положительный заряд по абсолютной величине равен заряду электрона. Масса протона равна 1,6726×10^-27 кг. Протон как частица, входящая в состав атомных ядер, открыт Резерфордом в 1919 г.

Для экспериментального определения масс атомных ядер применялись и применяются масс-спектрометры. Принцип масс-спектрометрии, впервые предложенный Томсоном (1907 г.), заключается в использовании фокусирующих свойств электрических и магнитных полей по отношению к пучкам заряженных частиц. Первые масс-спектрометры с достаточно высокой разрешающей способностью были сконструированы в 1919 г. Ф.У. Астоном и А. Демпстером. Принцип действия масс-спектрометра показан на рис. 1.3.

Так как атомы и молекулы электрически нейтральны, их необходимо предварительно ионизировать. Ионы создаются в ионном источнике путем бомбардировки быстрыми электронами паров исследуемого вещества и затем, после ускорения в электрическом поле (разность потенциалов V) выходят в вакуумную камеру, попадая в область однородного магнитного поля B. Под его действием ионы начинают двигаться по окружности, радиус которой r можно найти из равенства силы Лоренца и центробежной силы:

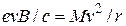, (1.5)

где М – масса иона. Скорость движения ионов v определяется соотношением

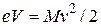. (1.6)

Исключая скорость v из (1.5) и (1.6), найдем, что

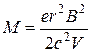. (1.7)

Ускоряющую разность потенциалов V или напряженность магнитного поля B можно подобрать так, чтобы ионы с одинаковыми массамипопадали в одно и то же место (r) фотопластинки или другого позиционно-чувствительного детектора. Тогда, находя максимум масс-спектрометрического сигнала и пользуясь формулой (1.7), можно определить и массу иона M.[4]

Развитие техники масс-спектрометрии позволило подтвердить высказанное еще в 1910 г. Фредериком Содди предположение о том, что дробные (в единицах массы атома водорода) атомные массы химических элементов объясняются существованием изотопов – атомов с одинаковым зарядом ядра, но различными массами. Благодаря пионерским исследованиям Астона было установлено, что большинство элементов действительно состоит из смеси двух или более природных изотопов. Исключением являются сравнительно немногие элементы (F, Na, Al, P, Au и др.), называемые моноизотопными. Число природных изотопов у одного элемента может достигать 10 (Sn). Кроме того, как выяснилось позже, у всех без исключения элементов имеются изотопы, обладающие свойством радиоактивности. Большинство радиоактивных изотопов не встречается в природе, они могут быть получены лишь искусственно. Элементы с атомными номерами 43 (Tc), 61 (Pm), 84 (Po) и выше имеют только радиоактивные изотопы.

Принятая сегодня в физике и химии международная атомная единица массы (а.е.м.) – это 1/12 массы наиболее распространенного в природе изотопа углерода: 1 а.е.м. = 1,66053873×10^-27 кг.[5] Она близка к атомной массе водорода, хотя и не равна ей. Масса электрона составляет примерно 1/1800 а.е.м. В современных масс-спектрометрах относительная погрешность измерения массы ΔM/M ≈ 10^–7-10^–8, что позволяет измерять разности масс на уровне 10^–6-10^–7 а.е.м.

Атомные массы изотопов, выраженные в а.е.м., являются почти точно целочисленными. Таким образом, каждому атомному ядру можно приписать его массовое число А (целое), например Н-1, H-2, Н-3,[6] С-12, О-16, Cl-35, Cl-37 и т.п. Последнее обстоятельство возродило на новой основе интерес к гипотезе У. Проута (1816 г.), согласно которой все элементы построены из водорода.[7]

1.4. Открытие нейтрона. Протонно-нейтронная теория. После открытия атомного ядра довольно долго (около 20 лет) считалось, что ядро состоит из протонов и электронов: А протонов и А – Z электронов. Мысль об этом казалась естественной, так как при радиоактивном распаде наблюдалось испускание электронов (β-частиц). При этом, так как масса протона много больше массы электрона, удавалось объяснить не только заряд, но и массу ядра. Но у протонно-электронной модели были и противоречия. С развитием квантовой механики все очевиднее становилась несопоставимость «размеров» ядра и электрона. Кроме того, вскрылось и другое несоответствие, получившее название «азотной катастрофы». Было установлено, что спин ядра азота с А = 14 равен 1, т.е. имеет целочисленное значение, тогда как модель предсказывала полуцелое значение, как и для всякой системы, состоящей из нечетного числа фермионов.[8] Это заставило ввести дополнительные предположения о том, что электроны в ядре находятся в некотором особом связанном состоянии. Интересно, что Резерфорд еще в 1920 г. высказал гипотезу о существовании «нейтрона» – комбинации из тесно связанных электрона и протона.

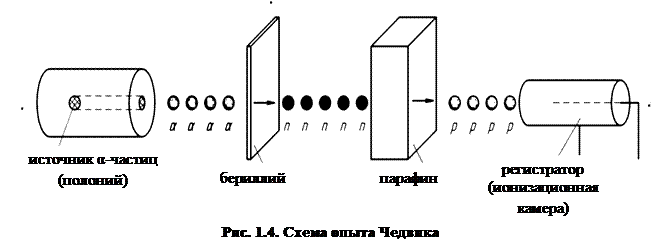В последующие годы было сделано много попыток доказать существование постулированного Резерфордом нейтрона. Это удалось только в 1932 г. Дж. Чедвик исследовал свойства сильно проникающего излучения, возникающего при бомбардировке α-частицами бериллия или бора. Вначале предполагалось, что это очень жесткие[9] γ-лучи. Однако, когда выяснилась способность неизвестного излучения выбивать быстрые протоны из веществ, содержащих водород (рис. 1.4), от такого предположения пришлось отказаться, т.к. оно противоречило законам сохранения энергии и импульса. Чедвик показал, что все опытные факты легко объясняются, если предположить, что неизвестное излучение представляет собой поток незаряженных частиц с массой, примерно равной массе протона. В первых расчетах Чедвика масса нейтрона оказалась лишь немногим меньше суммы масс протона и электрона, m_p + m_e, и вначале, в духе гипотезы Резерфорда, Чедвик считал нейтрон составной частицей. Однако более поздние точные измерения показали, что нейтрон примерно на 1,5m_e тяжелее атома водорода. Согласно современным представлениям, нейтрон (n) – такая же элементарная частица, как и протон.[10] Ее электрический заряд равен нулю, а спин, как у протона и электрона, ½.

После открытия нейтрона протонно-электронная гипотеза строения ядра была отброшена и заменена протонно-нейтронной (Д.Д. Иваненко, В. Гейзенберг, Э. Майорана, 1932 г.). Атомное ядро состоит из протонов и нейтронов, совместно именуемых нуклонами. Число протонов в ядре равно атомному номеру Z соответствующего химического элемента, а сумма чисел протонов и нейтронов равна массовому числу А. Следовательно, число нейтронов N = A – Z. Разновидность атомов химического элемента с определенным протонно-нейтронным составом ядра называют нуклидом. В качестве символа нуклида используют обозначение 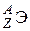, где Э – символ элемента ( 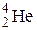, , 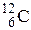, 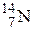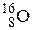и т.п.). Часто атомный номер Z опускают, так как он дублирует символ Э. Таким образом, ядро ⁴He (α-частица) содержит 2 протона и 2 нейтрона. Ядро ¹⁴N состоит из 7 протонов и 7 нейтронов, т.е. содержит 14 нуклонов, спин каждого из которых равен ½. Суммарный спин такой системы должен быть целочисленным, что и наблюдается на самом деле.

Ядра с одинаковым Z называют изотопами, с одинаковым N – изотонами, с одинаковым А – изобарами.