Электрический заряд ядра
Ядро имеет положительный электрический заряд, который образуют протоны. Число протонов Z называют зарядом ядра, подразумевая, что он равен величине Ze Кл, где е = 1,602 ×10-19 Кл (4,8×10-10 CГCЕ ед.) – абсолютная величина элементарного электрического заряда.
Заряд ядра был определен в 1913 г. Мозли, который измерил с помощью дифракции на кристаллах длину λ волны характеристического рентгеновского излучения для ряда химических элементов, следующих друг за другом в периодической системе элементов. Измерения показали, что λ изменяется дискретным образом от некоторой целой величины Z, которая совпадает с порядковым номером элемента и изменяется на единицу при переходе от элемента к соседнему элементу в периодической системе, а для водорода равна единице. Мозли интерпретировал эту величину как заряд ядра и установил, что (закон Мозли):
 aZ – b, aZ – b,
| (1.2.1) |
где a и b – константы для данной серии рентгеновского излучения и не зависят от элемента.
Закон Мозли определяет заряд ядер химического элемента косвенным образом. Прямые опыты по измерению заряда ядер на основе закона Кулона были выполнены Чедвиком в 1920 г. В 1911 г. Резерфорд, используя закон Кулона, получил формулу
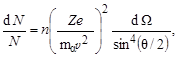
|  (1.2.2) (1.2.2)
|
 которая позволила объяснить экспериментальные результаты по рассеянию α-частиц на тяжелых ядрах, что, в конечном итоге, привело в 1911 г. к открытию атомного ядра и созданию ядерной модели атома. В формуле (1.2.2): N – количество α-частиц, падающих в единицу времени на рассеиватель; dN – количество рассеянных в единицу времени α-частиц в телесный угол dΩ под углом θ; Ze и n – заряд ядер рассеивателя и их концентрация; v и mα – скорость и масса α-частиц. Схема опыта Чедвика приведена на рис. 1.2.1. Рассеиватель α-частиц в виде кольца (заштриховано на рис 1.2.1) размещался сносно и на равных расстояниях между источником И и детектором α-частиц Д. При измерении количества dN рассеянных α-частиц отверстие в кольце закрывалось экраном, который поглощал прямой пучок α‑частиц из источника в детектор. Детектор регистрировал только α‑частицы, рассеянные в телесный угол dΩ под углом
которая позволила объяснить экспериментальные результаты по рассеянию α-частиц на тяжелых ядрах, что, в конечном итоге, привело в 1911 г. к открытию атомного ядра и созданию ядерной модели атома. В формуле (1.2.2): N – количество α-частиц, падающих в единицу времени на рассеиватель; dN – количество рассеянных в единицу времени α-частиц в телесный угол dΩ под углом θ; Ze и n – заряд ядер рассеивателя и их концентрация; v и mα – скорость и масса α-частиц. Схема опыта Чедвика приведена на рис. 1.2.1. Рассеиватель α-частиц в виде кольца (заштриховано на рис 1.2.1) размещался сносно и на равных расстояниях между источником И и детектором α-частиц Д. При измерении количества dN рассеянных α-частиц отверстие в кольце закрывалось экраном, который поглощал прямой пучок α‑частиц из источника в детектор. Детектор регистрировал только α‑частицы, рассеянные в телесный угол dΩ под углом 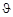 к падающему пучку α-частиц. Затем кольцо перекрывалось экраном с отверстием, и измерялась плотность тока α-частиц в точке расположения детектора. Используя полученные данные, рассчитывалось количество N α‑частиц, падающих на кольцо в единицу времени. Таким образом, если известна энергия α-частиц, испускаемых источником, без труда определяется величина Z в формуле (1.2.2). Некоторые из результатов, полученные Чедвиком, приведены в таблице 1.2.1 и не оставляют сомнений в справедливости закона Мозли.
к падающему пучку α-частиц. Затем кольцо перекрывалось экраном с отверстием, и измерялась плотность тока α-частиц в точке расположения детектора. Используя полученные данные, рассчитывалось количество N α‑частиц, падающих на кольцо в единицу времени. Таким образом, если известна энергия α-частиц, испускаемых источником, без труда определяется величина Z в формуле (1.2.2). Некоторые из результатов, полученные Чедвиком, приведены в таблице 1.2.1 и не оставляют сомнений в справедливости закона Мозли.
 §1.3. Масса ядра и масса атома
§1.3. Масса ядра и масса атома
Масса ядра является одной из важных характеристик. Массу ядра нуклида данного состава (А,Z) будемобозначать М(А,Z) или М(АХ), а массу соответствующего нуклида Мат.
В ядерной физике, так же как и в атомной физике, для измерения масс широко используется атомная единица массы (а.е.м.):
1а.е.м. = 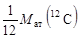 = 1,6605×10-24 г. = 1,6605×10-24 г.
| (1.3.1) |
В этих единицах:
масса протона mp = 1,6726×10-24 г = 1,007825 а.е.м.;
масса нейтрона mn = 1,6749×10-24 г = 1,008665а.е.м.
Видно, что 1 а.е.м. близка к массе нуклона, что очень удобно.
Масса электрона me много меньше массы протона, mp /me = 1836.
Масса нуклида, выраженная в атомных единицах массы, является относительной величиной и называется атомной массой. Атомная масса имеет специальное обозначение Аr (не путать с массовым числом А!).
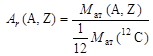
| (1.3.2) |
Величина
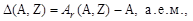
| (1.3.3) |
называется избытком массы нуклида и имеет большое значение в ядерной физике. Формула (1.3.3) выражает различие между понятиями атомной массы и массового числа. Однако величина Δ(A,Z) << 1 для всех нуклидов и поэтому даже для самых легких ядер атомная масса примерно равна массовому числу. Это послужило одной из причин выбрать пару чисел (A,Z) для идентификации состава ядра нуклида.
Связь между массой любого тела и его энергией покоя дается формулой:
 , ,
| (1.3.4) |
где с = 2,998×1010 см/с - скорость света в вакууме. На этом основании в ядерной физике для измерения массы, так же как и энергии, часто используется единица энергии электронвольт (эВ) и производные от нее:
1 кэВ (килоэлектронвольт) = 103 эВ
1 МэВ (мегаэлектронвольт) = 106 эВ
1 ГэВ (гигаэлектронвольт) = 109 эВ.
Напомним, что 1 эВ – изменение энергии элементарного заряда е при прохождении им разности потенциалов равной 1 В.
Установим соответствие между 1 а.е.м. и 1 эВ. Из формулы (1.3.4):
1а.е.м.= 1,6605×10-27×(2,998×108)2 = 1,492×10-10 Дж,
а из определения электронвольта:
1эВ = 1,602×10-19×1 = 1,602×10-19 Дж.
Таким образом, из последних двух соотношений следует, что
1 а.е.м. =  ≈ 931,5 МэВ,
≈ 931,5 МэВ,
и соответственно
mp =1,007825 а.е.м. = 1,6726×10-24 г = 938,2 МэВ,
mn = 1,008665а.е.м. = 1,6749×10-24 г = 939,5 МэВ,
me= 5,4859×10-4а.е.м. = 9,1096×10-28 г = 0,511 МэВ.
В ядерной физике обычно пользуются не массами ядер, а массами нуклидов. Это вызвано тем, что невозможно измерить непосредственно массу ядер без связанных с ними электронов, за исключением легчайших. Масса нуклида в пределах точности современных методов измерения масс равна сумме масс ядра и электронов, составляющих атом, хотя в принципе масса нуклида есть
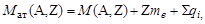
| (1.3.5) |
 где Σqi – энергия связи электронов в атоме, Σqi ≈ 13,6×Z эВ. Таким образом, энергия связи электронов с ядром более чем в 107 раз меньше энергии покоя нуклида и практически не влияет на его массу.
где Σqi – энергия связи электронов в атоме, Σqi ≈ 13,6×Z эВ. Таким образом, энергия связи электронов с ядром более чем в 107 раз меньше энергии покоя нуклида и практически не влияет на его массу.
Массы нуклидов определяют с помощью приборов, которые называются масс-спектрометрами. Схема устройства простейшего масс-спектрометра изображена на рис. 1.3.1. В ионном источнике ИИ создаются положительные ионы нуклидов, массу Мi которых необходимо измерить. Ионы, имеющие электрический заряд qi, поступают через отверстие в ускоряющее электрическое поле, создаваемое приложенной между ИИ и Д1 разностью потенциалов U, после прохождения которой ионы приобретают кинетическую энергию
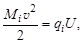
| (1.3.6) |
и со скоростью v поступают в пространственно однородное и постоянное магнитное поле с индукцией В, вектор которой перпендикулярен плоскости чертежа и направлен на читателя. На ион в магнитном поле действует сила Лоренца
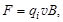
| (1.3.7) |
которая создает центростремительное ускорение v2/R, направленное к точке О, под действием которого ион будет двигаться по окружности радиуса R. Таким образом,
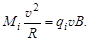
| (1.3.8) |
Исключив из (1.3.6) и (1.3.8) скорость v, находим, что величина массы иона
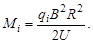
| (1.3.9) |
Окружность нужного радиуса R задается положением диафрагм Д1, Д2 и Д3 . Подбирая величины U и В добиваются того, чтобы пучок ионов попадал на коллектор К, что фиксируется по максимуму тока ионов на коллекторе. Таким образом устанавливается, что ион движется по окружности радиуса R и вычисляется масса иона. Если известна кратность ионизации то, вычитая из массы иона известную суммарную массу электронной оболочки, получают массу ядра.
Дата добавления: 2021-07-22; просмотров: 996;











