Дебаевский радиус (дебаевская длина) экранирования.
Рассмотрим газообразную среду, состоящую из ионов и электронов. Распределение заряженных частиц в пространстве в достаточно большом объеме должно быть достаточно равномерным. В противном случае возникло бы электрическое поле, стремящееся сблизить разноименные заряды и сгладить неравномерность распределения.
Рассмотрим распределение плотности заряда в окрестности произвольно выбранной заряженной частицы. Такая частица будет отталкивать одноименные заряды и притягивать заряды разноименного знака (рис. 22.1).
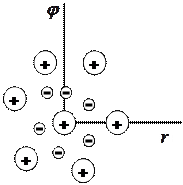
| Найдем зависимость потенциала результирующего поля, созданного выбранной (пробной) частицей и ее окружением. Запишем теорему Гаусса в дифференциальной форме
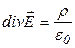 (*).
Воспользовавшись связью напряженности и потенциала (*).
Воспользовавшись связью напряженности и потенциала 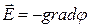 , получим: , получим:
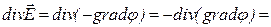
|
| Рис. 22.1 |
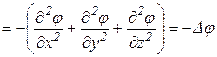 (**), где
(**), где 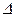 - оператор Лапласа.
- оператор Лапласа.
Сравнивая (*) с (**) получаем уравнение Пуассона 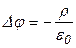 . Плотность заряда
. Плотность заряда 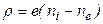 , где
, где 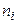 и
и 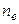 - концентрация ионов и электронов соответственно.
- концентрация ионов и электронов соответственно.
При максвелловском распределении по скоростям связь потенциала и концентрации ионов определяется формулой Больцмана
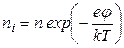
где 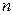 - средняя концентрация заряженных частиц (ионов) в невозмущенной области (не возмущенной полем данного заряда).
- средняя концентрация заряженных частиц (ионов) в невозмущенной области (не возмущенной полем данного заряда).
Для электронов с учетом знака соответственно (плазму считаем равновесной):
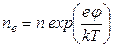
где 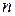 средняя концентрация электронов в невозмущенной области. (В силу квазинейтральности
средняя концентрация электронов в невозмущенной области. (В силу квазинейтральности 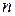 для ионов и электронов – одна и та же величина.)
для ионов и электронов – одна и та же величина.)
Подставляем последние выражения в уравнение Пуассона:
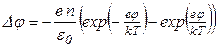 .
.
В случае низкотемпературной плазмы 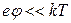 экспоненты можно разложить в ряд:
экспоненты можно разложить в ряд:
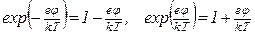 , тогда
, тогда 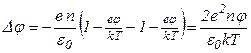 .
.
Решение этого уравнения:
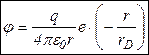
где 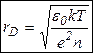 - радиус Дебая.
- радиус Дебая.
Физический смысл радиуса Дебая: на расстоянии, равном 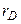 , потенциал спадает в
, потенциал спадает в 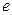 раз, действие поля заряженной частицы на окрестные частицы компенсируется (поле заряженной частицы экранируется).
раз, действие поля заряженной частицы на окрестные частицы компенсируется (поле заряженной частицы экранируется).
(Замечания. 1. Характерная длина 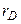 была впервые введена Дебаем при рассмотрении теории сильных электролитов. В дальнейшем это понятие было перенесено в физику плазмы. 2. Вывод был получен при
была впервые введена Дебаем при рассмотрении теории сильных электролитов. В дальнейшем это понятие было перенесено в физику плазмы. 2. Вывод был получен при 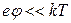 , но оказывается, что и при
, но оказывается, что и при 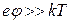 характерный масштаб нарушения квазинейтральности (
характерный масштаб нарушения квазинейтральности ( 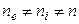 ) имеет порядок дебаевского радиуса.)
) имеет порядок дебаевского радиуса.)
Рассмотрим другой, упрощенный подход к решению задачи о масштабе нарушения квазинейтральности.
Выделим в плазме плоский слой площадью 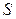 и толщиной
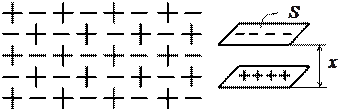
и толщиной 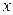 и предположим, что заряды одного знака вышли на одну из плоскостей, ограничивающих слой, т.е. произошло разделение зарядов (например, за счет тепловых флуктуаций) (рис. 22.2).
и предположим, что заряды одного знака вышли на одну из плоскостей, ограничивающих слой, т.е. произошло разделение зарядов (например, за счет тепловых флуктуаций) (рис. 22.2).
| Такое самопроизвольное разделение зарядов возможно, если потенциальная энергия заряженной частицы и ее кинетическая энергия теплового движения равны, т.е.
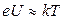 (*). (*).
|
| Рис. 22.2 |
Плоский слой можно рассматривать как конденсатор, напряжение на котором 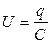 , заряд равен заряду электронов, ушедших вследствие тепловой флуктуации на одну из плоскостей рассматриваемого слоя из объема слоя, т.е.
, заряд равен заряду электронов, ушедших вследствие тепловой флуктуации на одну из плоскостей рассматриваемого слоя из объема слоя, т.е. 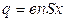 , а емкость
, а емкость 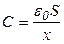 . Подставляя это выражение в (*), получим
. Подставляя это выражение в (*), получим
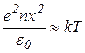 .
.
Получаем характерный размер области, в которой возможно отклонение от нейтральности, – дебаевскую длину
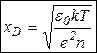
К такой же характерной длине мы пришли, рассматривая вопрос об экранировании электрического поля в плазме ( 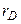 ).
).
Роль длины Дебая как радиуса экранирования и как пространственного масштаба разделения зарядов выражена определением плазмы Ленгмюра: совокупность свободно движущихся разноименно заряженных частиц, т.е. ионизированный газ, называется плазмой, если длина Дебая мала по сравнению с линейным размером объема, занимаемого газом.
Пока радиус Дебая мал по сравнению с размером 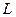 изучаемой системы
изучаемой системы 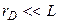 , процессы нарушения квазинейтральности носят локальный и кратковременный характер.
, процессы нарушения квазинейтральности носят локальный и кратковременный характер.
Дата добавления: 2017-01-26; просмотров: 8410;











