Интегрирование некоторых тригонометрических выражений.

Рациональные функции от двух переменных.

Определение: многочленом степени n от двух переменных x, y, называется выражение 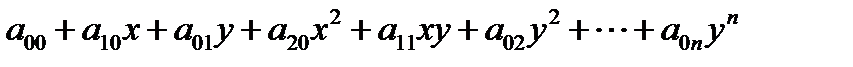, в котором через 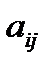обозначены некоторые постоянные числа, часть из которых может быть равна нулю, а среди 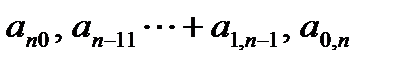есть хотя бы одно число, отличное от нуля.

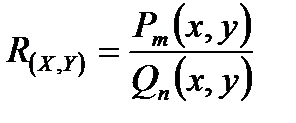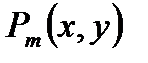Рациональной функцией от двух переменных x, y, называется выражение вида: , где -многочлен степени m, от переменных x, y. 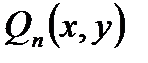-многочлен степени n, от переменных x, y.

Относительно рациональных функций от двух переменных справедливо утверждение.

Если 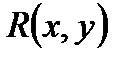- рациональная функция от двух переменных

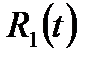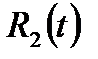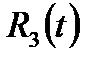, , - рациональные функции от одной переменной t,

то выражение R( 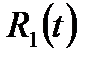, 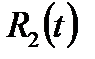) 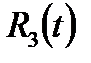является рациональной функцией от одной переменной t.

Интегрирование некоторых тригонометрических выражений.

Рассмотрим вопрос об интегрировании выражения 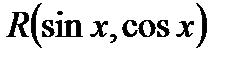, где 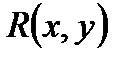- некоторая рациональная функция от двух переменных. Покажем, что 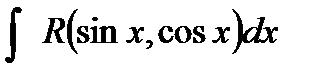рационализируется с помощью универсальной тригонометрической подстановкой, 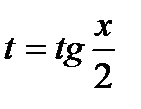, выразим величины sin x и cos x через :

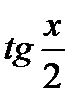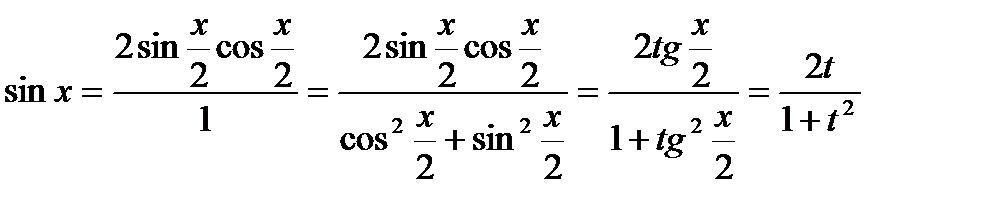
аналогично легко получить выражения cos x:

,

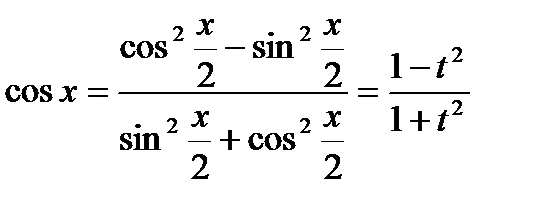видим, что величины sin x и cos x рационально выражаются через переменную t, осталось показать, что дифференциал dx также рационально выражается через переменную t.

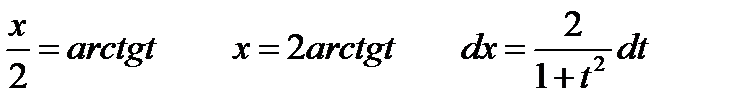
Таким образом, видим, что рассматриваемый интеграл сводится к рациональной функции от одной переменной.

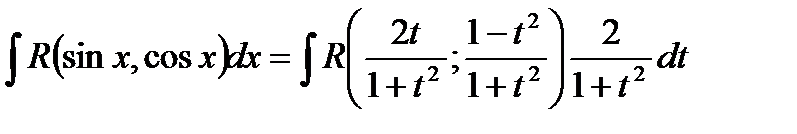
Пример: Вычислить интеграл.

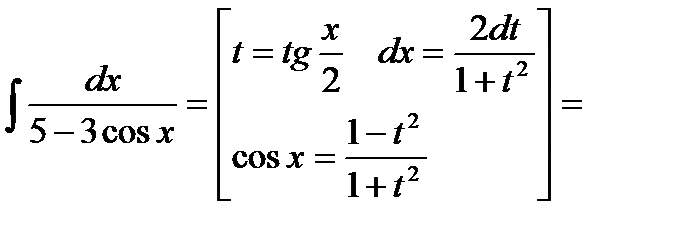
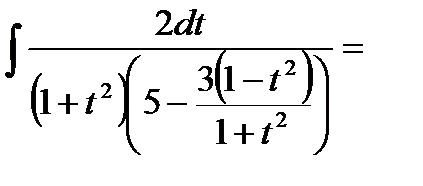
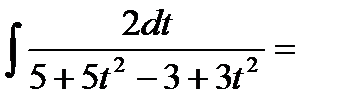
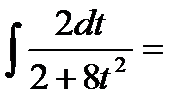
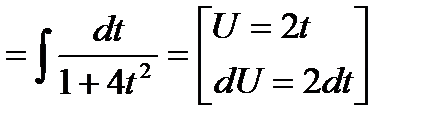
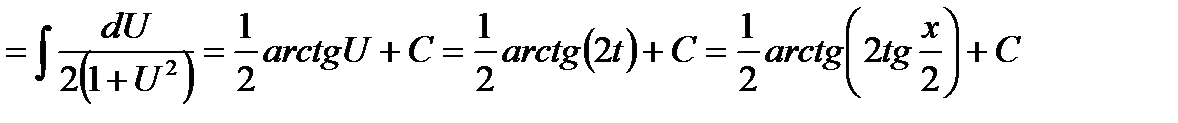
Не смотря на то, что универсальная тригонометрическая подстановка рационализирует широкий класс функций её применение достаточно громадно, часто удается вычислить конкретный интеграл без её применения.