Интегрирование квадратичных иррациональностей.
Квадратичной иррациональностью называется выражение вида: 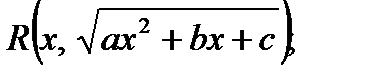 где a, b, c – некоторые вещественные числа, R(x, y)-рациональная функция от двух переменных.
где a, b, c – некоторые вещественные числа, R(x, y)-рациональная функция от двух переменных.
Будем считать, что квадратный трехчлен 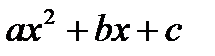 не имеет кратных корней. Покажем, что интеграл от выражения такого типа рационализируется с помощью подстановок Эйлера.
не имеет кратных корней. Покажем, что интеграл от выражения такого типа рационализируется с помощью подстановок Эйлера.
Рассмотрим сначала случай, когда квадратный трехчлен не имеет действительных корней. Так как трехчлен 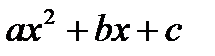 стоит под знаком квадратного радикала, то его значения должны быть не отрицательны
стоит под знаком квадратного радикала, то его значения должны быть не отрицательны 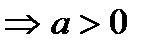 . Покажем, что в этом случае может быть использована первая подстановка Эйлера.
. Покажем, что в этом случае может быть использована первая подстановка Эйлера.
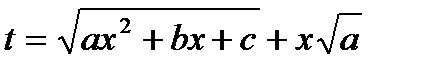
найдем значения х через величину t.
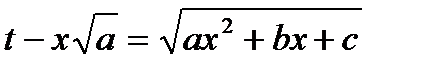 ,
, 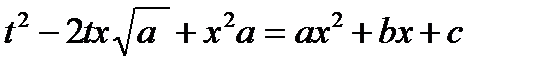 ,
, 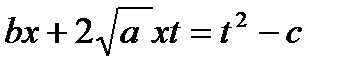 ,
, 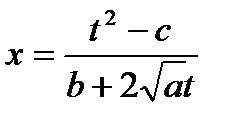 .
.
Найдем величину дифференциала dx:
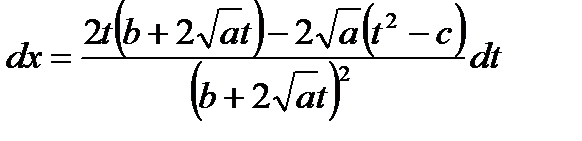 ,
, 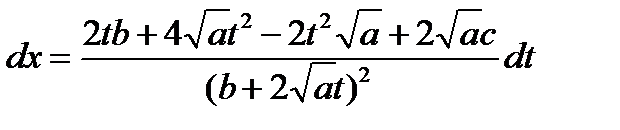 .
.
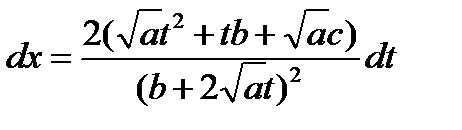
То есть дифференциал х является рациональной функцией переменой t.
Найдем выражение для квадратного радикала:
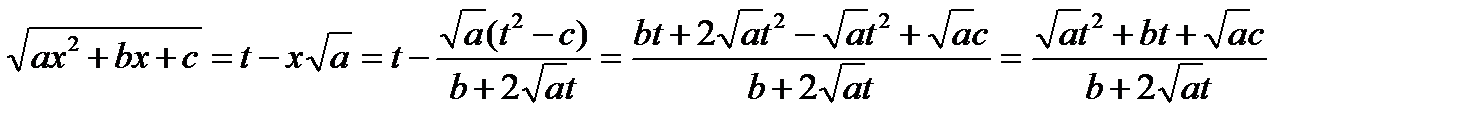
Таким образом, квадратичная рациональность интеграла принимает вид:
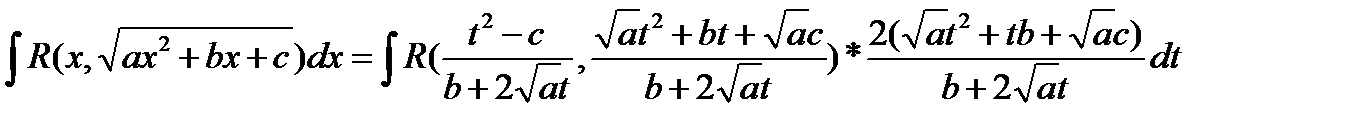
Если величина С неотрицательна, то для рационализации может быть использована вторая подстановка Эйлера.
 введем новую переменную
введем новую переменную
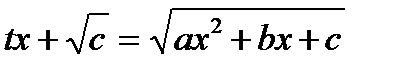 ,
, 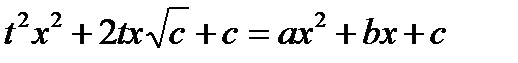 ,
, 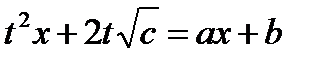 ,
,
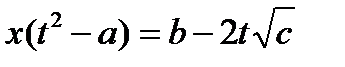
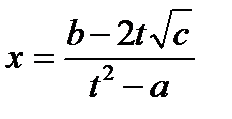
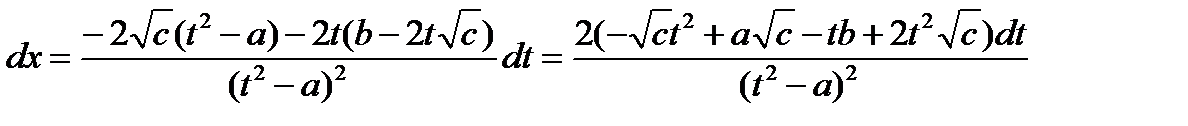
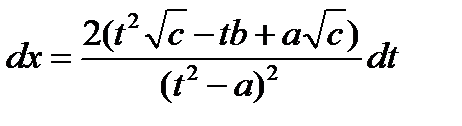 ,
, 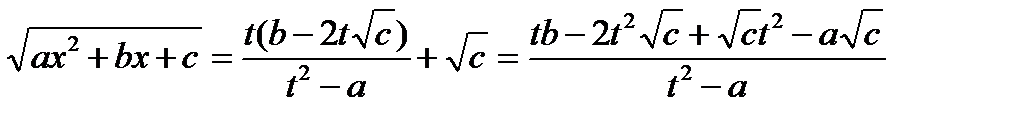
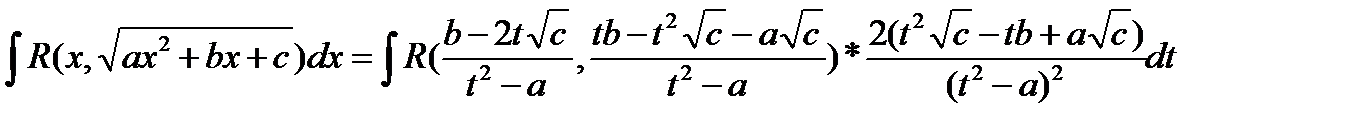
Видим, что вторая подстановка Эйлера также рационализирует квадратичную иррациональность.
Рассмотрим случай, когда 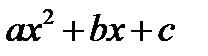 имеет действительные корни, то есть многочлен можно представить в виде:
имеет действительные корни, то есть многочлен можно представить в виде: 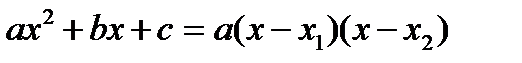 , где
, где 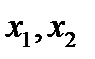 - корни квадратного трехчлена. В этом случае рационализация достигается с помощью третьей подстановки Эйлера, которая имеет вид:
- корни квадратного трехчлена. В этом случае рационализация достигается с помощью третьей подстановки Эйлера, которая имеет вид:
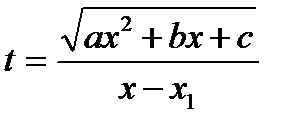 ,
, 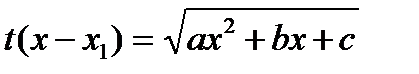 ,
, 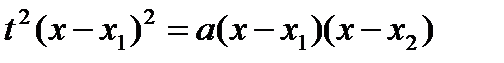 ,
, 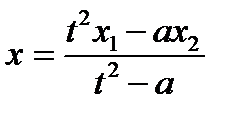
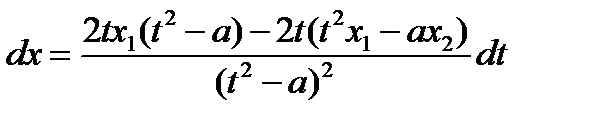 ,
, 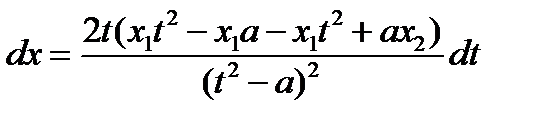 ,
, 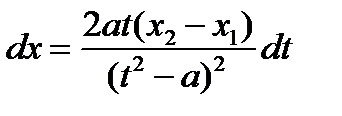
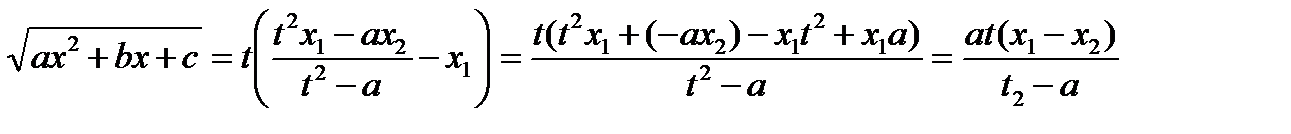
Таким образом, квадратичная иррациональность примет вид:
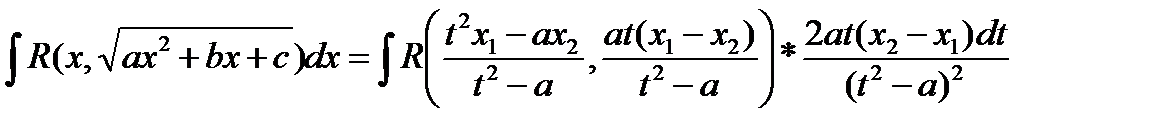
Пример: Вычислить интеграл 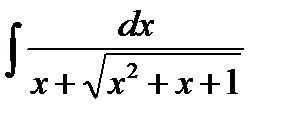
Рассмотрим квадратный трехчлен 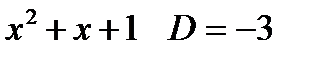 . Квадратный трёхчлен не имеет действительных корней. Используем первую подстановку Эйлера.
. Квадратный трёхчлен не имеет действительных корней. Используем первую подстановку Эйлера.
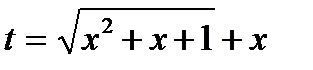 ,
, 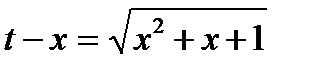 ,
, 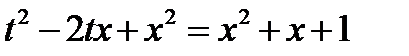 ,
, 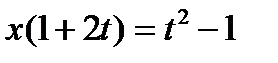 ,
, 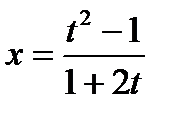 ;
;
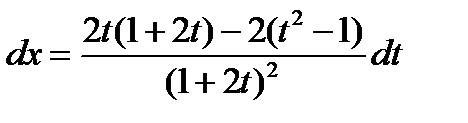 ,
, 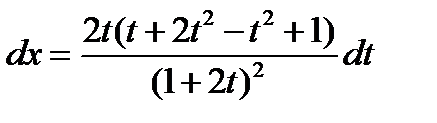 ,
, 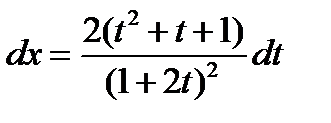
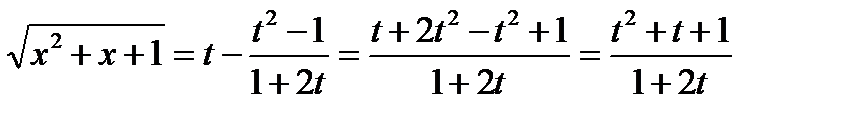
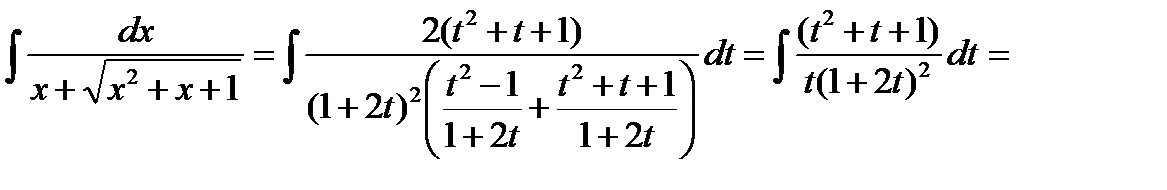
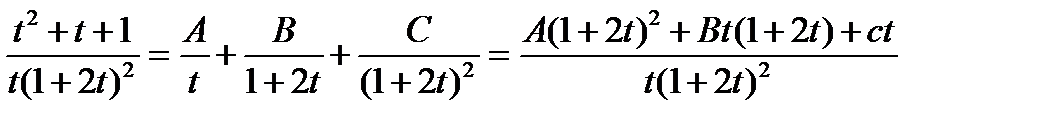
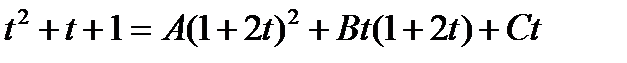
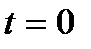 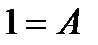
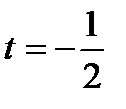 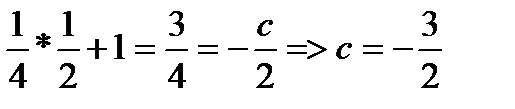
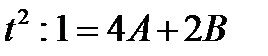 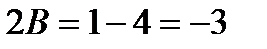 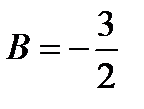
|
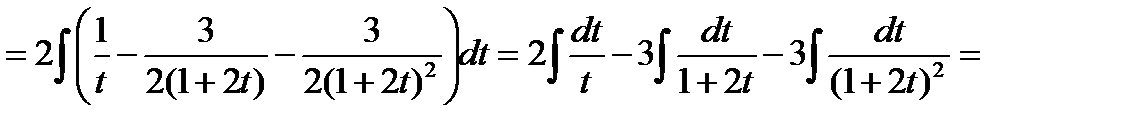
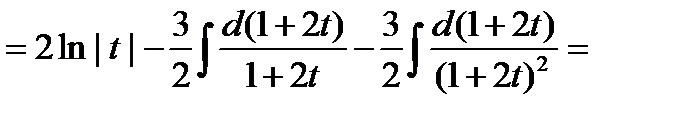
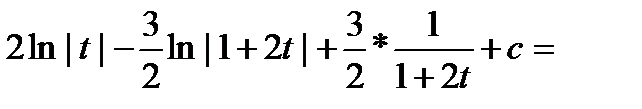
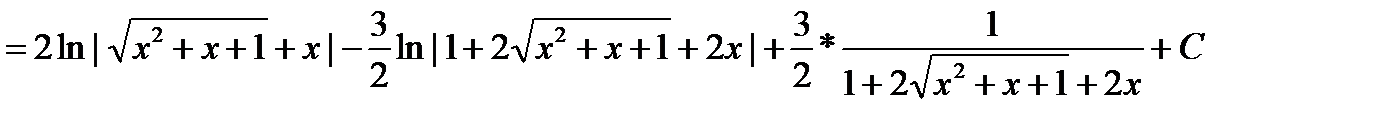
Дата добавления: 2017-06-13; просмотров: 3344;











