Расположение точек на карте — информация к размышлению

На что можно опереться в процессе интерпрета­ции ККШ? Исходные данные, — это конфигурация, или структура точек. В них содержатся сведения о значениях измеряемых величин и очень важная информация об их временной последовательности. Как известно, сам У. Шухарт предложил очень простое операциональное определение специальных причин вариабельности: выход точки на контрольной карте за границу верхнего или нижнего контрольного предела. В дальнейшем, однако, по мере того, как контрольные карты все шире использовались в промышленности, на практике все чаще возникала ситуация, когда все точки находились в зо­не между верхним и нижним пределами, но из картинки было ясно, что с процессом что-то происходит (например, процесс имеет явную тенденцию к росту/ снижению, процесс носит периодический характер и т. п.). Вот почему перечень признаков, по которым можно визуально оценить статистическую стабиль­ность (управляемость) процесса со временем был расширен: в него были добавлены так называемые неслу­чайные (особые) структуры, серии и т. п. Рассмотрим теперь эти признаки более подробно.

Начнем с одного общего важного замечания. Дело в том, что само представление о случайности уместно только до того момента, когда произошли те или иные события. Всякое уже произошедшее событие неслучайно уже в силу того, что оно случилось. Эта проблема создает принципиальные трудности в интерпретации ККШ. Ясно, что «подозрительные» структуры точек могут служить лишь поводом для вы­движения гипотез, и не более того. А проверка этих гипотез — следующий этап. Она предполагает исполь­зование широкой гаммы статистических методов и цикла Шухарта—Деминга.

Есть несколько подходов к выделению особых структур точек. Вот набор правил обнару­жения специальных причин вариаций, приведенный в одной из лучших книг на тему статистического уп­равления процессами (СУП) на русском языке.

1. Выход точек за контрольные пределы(рис. 20).

Рис.20 Выход за контрольные пределы

2. Серия— это такое состояние, когда точки неиз­менно оказываются по одну сторону от средней ли­нии, число таких точек называется длиной серии (рис. 21).

Рис.21. Понятие серии

Серия длиной в семь точек рассматривается как ненормальная.

Кроме того, ситуацию следует рассматривать как ненормальную, если:

а) не менее 10 из 11 точек оказываются по одну сторону от центральной линии;

б) не менее 12 из 14 точек оказываются по одну сторону от центральной линии;

в) не менее 16 из 20 точек оказываются по одну сторону от центральной линии.

3. Тренд (дрейф).Если точки образуют непрерывно повышающуюся или понижающуюся кривую, то гово­рят, что имеет место тренд (рис. 22).

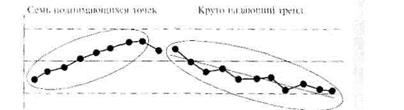
Рис. 22. Понятие тренда

4. Приближение к контрольным пределам.Рассмат­риваются точки, которые приближаются к 3-сигмо-вым контрольным пределам, причем, если из трех последовательных точек две оказываются за 2-сигмовы-ми линиями, то такой случай надо рассматривать как ненормальный (рис. 23).

Рис. 23 Приближение к контрольным пределам.

Приближение к центральной линии.Если на кон­трольной карте большинство точек концентрируется в пространстве, ограниченном 1,5-сигмовыми ли­ниями, делящими пополам расстояние между цент­ральной линией и каждой из контрольных границ, то причина, скорее всего, в неподходящем способе разбиения данных на подгруппы.

Приближение к центральной линии не всегда оз­начает, что достигнуто контролируемое состояние. Зачастую такая карта указывает, что в подгруппах смешиваются данные различных распределений, что делает размах контрольных пределов слишком широ­ким. В этом случае надо изменить способ разбиения данных на подгруппы (рис. 24).

Рис.24 Приближение к центральной линии

6. Периодичность.Когда кривая имеет периодиче­скую структуру (то подъем, то спад) с примерно оди­наковыми интервалами времени, это тоже ненормаль­но (рис. 25).

Рис. 25. Понятие периодичность

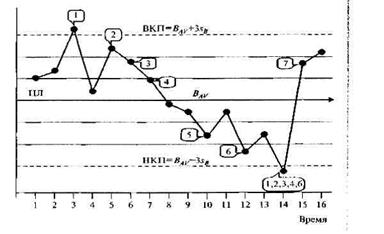
В разных источниках на­бор правил слегка отличается. Пожалуй, наиболее полный свод таких правил со ссылками на их источники приведен Д. Уилером. Эти пра­вила приведены в табл. 12, а примеры их проявления на контрольной карте отмечены на рис. 25 соответ­ствующими выносками (номер на выноске соответ­ствует номеру правила из табл. 12).

Таблица 12

П р и м е ч а н и е: Как пользоваться таблицей 12и рис 25,

Возьмем, например, правило 3: Из пяти последовательных точек четыре лежат выше (ниже) ЦЛ более чем на одно стандартное отклонение. Берем на рис. 25 выноску 3, отсчитываем от нее пять точек назади видим, что из этих пяти точек четыре лежат выше ЦЛ болей чем наодно стандартное отклонение (номера точек по порядку слева направо 2. 3, 5, 6), а одна - точка 4 — лежит внутри первой полосы, т.е. ниже на одно стандартное отклонение, от ЦЛ. Правила 2' и 3' — это просто модификация правил 2 и 3.

Латинской буквой В здесь обозначена интересующая нас характеристика, причем B_AV — это ее среднее значение, s_B — выбо­рочное стандартное отклонение, ВКП, НКП — верхний и нижний контрольные пределы, соответ­ственно

Рис.25 Поведение характеристик процесса

В современной литературе можно найти еще ряд правил. Например, весьма положительно оценивается правило числа серий. Серией на кон­трольной карте называют последовательность точек, находящуюся с одной стороны от центральной ли­нии (ЦЛ). При этом число точек нас не интересует: каждая группа с одной из сторон — это серия.

Итак, на рис. 25 три серии. Если бы четвертая по счету точка (между выносками 1 и 2) находилась ниже ЦЛ, то серий было бы пять. Если бы она находилась точно на ЦЛ, то серий было бы три (точка на ЦЛ пропускается). Границы на всех ККШрассчитываются всег­да по правилу ЦЛ ± З 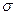, поэтому необходимо взять величи­ну расстояния между ЦЛ и верхним/нижним преде­лом, разделить полученное значение на три, отложить его вверх и вниз от ЦЛ и посмотреть, сколько точек попадают в полученную таким образом зону. Проде­лав эту несложную процедуру, мы получим, что за пределами ± 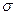от ЦЛ находится 11 точек. Если бы их было 10, то это была бы точно 1/3, а 11/30 — доста­точно близкое к 1/3 значение, т. е. по этому критерию с нашим процессом все нормально.

Важно не число дополнительных правил, сколько понимание того, откуда вообще эти правила берутся и как ими пользоваться. Приведем «10 заповедей» статистического управления процессами качества:

I.Не считай, что выход процесса важнее самого процесса.

II.Не смешивай проблемы управления процес­сом с проблемами его воспроизводимости.

III.Не используй точки, говорящие о специаль­ных причинах вариаций, для вычисления контрольных пределов.

IV.Не рисуй границы поля допуска на каждой контрольной карте.

V.Не подтасовывай данные, чтобы неуправ­ляемый процесс казался управляемым.

VI.Не поклоняйся правилу «точка за предела­ми контрольных границ».

VII.Не фальсифицируй исходные данные.

VIII.Не забывай о распределении выхода процесса.

IX.Не пренебрегай специальными причинами вариаций.

X.Не скрывай неуправляемый процесс от контролера, менеджера или потребителя.

Корректировка ККШДействия высшего руководства не всегда могут непосредственно отразиться на ККШ. Однако со­вершенствование системы рано или поздно обяза­тельно проявится в том, что вариабельность снизится. В этом, собственно, смысл совершенствования. Зна­чит, на ККШ это отразится в виде сужения разброса данных на картах, т. е. данные будут группироваться около центральной линии. И если, например, 14—15 точек подряд окажутся в пределах ± 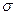относи­тельно среднего, то это, как известно, — признак возможного проявления особой причины вариации. В данном случае особая причина как раз и состоит в том, что сократилась системная вариация. Значит, пора корректировать карту. Для этого надо к уже обнаруженным 14—15 «подозрительным» точкам до­бавить, для верности, еще 5—10, после чего пересчитать среднее и контрольные пределы (границы) и нанести их на карты.

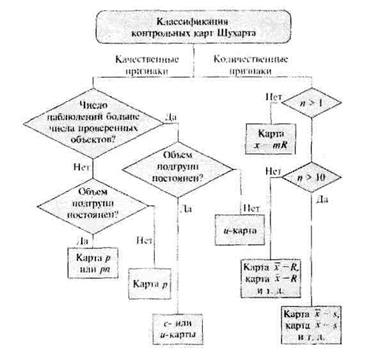
Типы контрольных картОбсудим вопрос о том, как выбирать тип контрольной карты Шухарта (ККШ). Дело в том, что, если тип выбранной карты не будет соответ­ствовать тому процессу, который необходимо диагнос­тировать и улучшать, то от примене­ния ККШ не получим того эффекта, на который рассчитывали. Есть некоторые общие ре­комендации, которые полезно иметь в виду. Прежде всего, типы ККШ различаются по тому, измеряется ли какой-либо параметр (характеристика) процесса или просто осуществлятся контроль качества по принципу «го­ден — негоден». В зависимости от этого принято де­лить ККШ на две группы: по количественным и каче­ственным признакам (см. рисунок 26)..

Карты по количественным при­знакам применяются при измерении какого-либо па­раметра (характеристики), когда в результате изме­рения получается некоторое число. Иногда эти карты называют картами для непрерывных величин.

Карты по качественным признакам применяются, когда измерения не проводятся, а сово­купность объектов разделяется на части: плохой — хороший, про­шел — не прошел, годный — дефектный или первый сорт — второй сорт — брак, и подсчитываем число объектов, попадающих в ту или иную категорию. Такие карты иногда называют картами для дискретных величин

Карты по количественным признакампринято делить на подтипы в зависимости от объема той подгруппы, какую измеряют в некоторой точке про­цесса (в некоторый момент времени). Этот объем обычно обозначают через n Если n = 1, то рекомендуется использовать ККШ, которая называется «картой индивидуальных значений и скользящего размаха» (сокращенно ее обозначают х — mR). Если п > 1, то, как легко видеть на схеме, возможно применение нескольких подтипов ККШ. Когда n мало, рекомендуется применять карты сред­него и размаха R. Когда n велико (больше 10), целесообразнее применять карты средне­го и стандартного отклонения s. При­чины такого разделения сложились исторически.

Рис. 26. Классификация контрольных карт

.

Пока не изобрели компьютеры, размах был удобной практической оценкой вариабельности данных, поскольку для выборок объема меньше 10 его информа­тивность в этом качестве близка к информативности стандартного отклонения. Однако при большом объе­ме подгруппы, размах теряет свою информативность, поскольку это всего лишь оценка, основанная на двух крайних значениях, и существенно уступает в этом качестве величине s. Сегодня, в эпоху всеобщей ком­пьютеризации, этот фактор перестал играть сколько-нибудь существенную роль для практики, но диффе­ренциация типов ККШ пока что сохраняется.

Карты по качественным признакам принято де­лить на два подвида в зависимости от соотношения числа наблюдений и объектов. Если число наблюдений превышает число объектов, т. е. в каждом объек­те возможно несколько дефектов – рn или их долей – р или же -с несоответствий и числа несоответствий на единицу измерений – u. При постоянном объеме подгруппы рекомендуется использовать карту с- или u-типа. При непостоянном объеме подгруппы следует использовать карту u-типа. Если же число наблюдений не превышает числа объектов, то при постоянном объеме подгрупп можно использовать, либо карту р-типа, либо карту pn-типа, тогда как при непостоянном объеме подгрупп реко­мендуется использовать только карту р-типа.

Примечание Более полные комментарии следует смотреть в ГОСТ Р 50779.42-99 (ИСО 8258—91) «Статистические методы. Контрольные кар­ты Шухарта» (табл. 2).

Резюмируем сказанное с помощью краткого опи­сания алгоритма построения контрольной карты.

1. Выбор показателя.

2. Выбор плана выборки.

3. Выбор типа карты.

4. Сбор данных.

5. Вычисление выборочных статистик.

6. Вычисление центральной линии.

7. Вычисление контрольных пределов.

8. Построение контрольной карты.

9. Оценка управляемости процесса.

10. В случае управляемости — оценка воспроизво­димости процесса.

11. Корректирующие действия в случае статисти­чески неуправляемого процесса.

12. Совершенствование системы.

13. Пересчет карты и т. д.
И так со всякой картой.