Методика синтеза РФ по аналоговому прототипу
Под синтезом ЦФ понимается получение требуемой передаточной функции и структуры фильтра по заданной его частотной или импульсной характеристики.
Синтез передаточной функции H(z) по заданной частотной характеристике Hd(jω) заключается в ее аппроксимации и определении коэффициентов передаточной функции. Используемые здесь методы разделяются на аналитические, итерационные и численные.
Аналитические методы обеспечивают решение задачи аппроксимации в замкнутой аналитической форме. К ним относятся методы синтеза рекурсивных фильтров (РФ) по данным аналогового фильтра-прототипа и в первую очередь метод билинейного преобразования.
Итерационные методы, сочетая аналитический и численный подходы, не дают однозначного соответствия параметров расчетных и заданных характеристик и требуют, как правило, ряда уточняющих процедур. Итерационными являются методы весовых функций и частотной выборки, используемые для синтеза нерекурсивных фильтров (НФ).
Численные методы основываются на непосредственной аппроксимации заданной частотной характеристики с минимальной погрешностью в соответствии с определенным критерием оптимальности.
По виду аппроксимируемой частотной характеристики H(jω) различают цифровые фильтры со ступенчатообразной амплитудно-частотной характеристикой (АЧХ) – фильтры нижних частот (ФНЧ), верхних частот (ФВЧ), полосно-пропускающие (ППФ), полосно-заграждающие (ПЗФ), многополосные (МПФ), и ЦФ с произвольной частотной характеристикой (рис. 9.8).
Так как частотные характеристики ЦФ периодичны по частоте с периодом ωд и их модуль (АЧХ) и аргумент (ФЧХ) обладают свойствами соответственно четной и нечетной симметрии относительно частот ω = 0 или 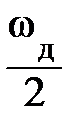 , то их достаточно задать в полосе частот (0 -
, то их достаточно задать в полосе частот (0 - 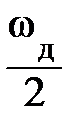 ) или полосе (0 – π) нормированных частот Ω = ωТд (рис. 9.8).
) или полосе (0 – π) нормированных частот Ω = ωТд (рис. 9.8).
Исходными данными для синтеза ЦФ по заданной частотной характеристике являются:
- частоты среза (или частоты полосы пропускания), задерживания или непропускания ωс, ωз, определяющие границы и значения полос пропускания, задерживания и переходных полос фильтра;
- допустимая неравномерность АЧХ фильтра в полосе пропускания an, как правило, задается в децибелах;
- минимальное затухание АЧХ в полосе задерживания aз, [дБ].
an = 20lg 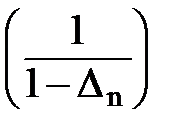 , aз = 10lg
, aз = 10lg 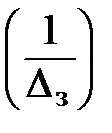
Здесь ∆n и ∆3 – отклонения расчетной АЧХ |H(jω)| от 1 в полосе пропускания и от нуля в полосе задерживания, в разах.
Рис. 9.8 – Примеры задания АЧХ ЦФ
Синтез РФ по аналоговому прототипу чаще всего осуществляется по методу билинейного преобразования или инвариантности частотных характеристик [5, 6, 7].
В этом методе синтезируемому ЦФ ставится в соответствии некоторый низкочастотный аналоговый фильтр-прототип (АФП) с передаточной функцией H(p) и частотной характеристикой H(jωа), однозначно связанными с передаточной функцией H(z) и частотной характеристикой H(jω) ЦФ.
Связь эта определяется прямой p = f(z) и обратной z = 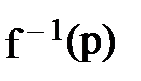 преобразующими функциями и соответствующими им при p = jωа и z = e jωТд преобразованиями частот ωа = f(ω), ω = f-–1(ωа) аналогового и цифрового фильтров. С помощью этих преобразований определяются требования к АФП, по которым хорошо разработанными методами синтезируется его передаточная функция H(p), преобразуемая затем в искомую передаточную функцию ЦФ H(z).
преобразующими функциями и соответствующими им при p = jωа и z = e jωТд преобразованиями частот ωа = f(ω), ω = f-–1(ωа) аналогового и цифрового фильтров. С помощью этих преобразований определяются требования к АФП, по которым хорошо разработанными методами синтезируется его передаточная функция H(p), преобразуемая затем в искомую передаточную функцию ЦФ H(z).
Эти преобразующие функции должны удовлетворять следующим условиям:
- левая P – полуплоскость p = σ + j ωа , σ < 0, в которой размещаются полюсы устойчивого АФП, должна однократно отображаться внутрь круга единичного радиуса |z| < 1, в котором на Z – плоскости размещаются полюсы устойчивого ЦФ, т.е. устойчивому АФП должен соответствовать устойчивый ЦФ;
- вся мнимая ось частот jωа АФП, ωа = (0 ± ∞), должна однократно, т.е. в один обход, отображаться на окружность единичного радиуса Z – плоскости ejωТд, ω = (0 ±  ), обеспечивая близость частотных характеристик обоих фильтров.
), обеспечивая близость частотных характеристик обоих фильтров.
Этим условиям отвечаютпростое билинейное преобразование и обобщенные билинейные преобразования.
Данное преобразование применимо в случае, когда аналоговый и цифровой фильтры одинакового типа. Ему соответствуют преобразующие функции и частотные преобразования вида:
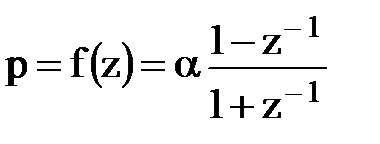 ;
; 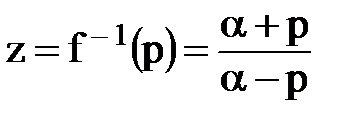 ; (9.15)
; (9.15)
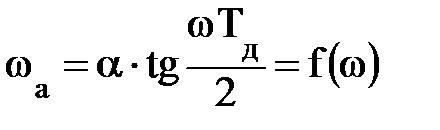 ;
; 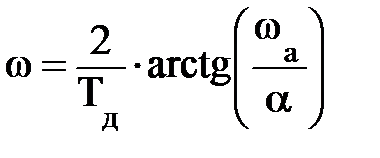 ,
,
где α – нормирующая константа.
Один из способов ее определения заключается в том, что минимальной частоте среза ЦФ ставится в соответствие единичное значение частоты среза нормированного АФП:
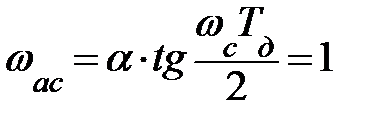 ,
,
отсюда 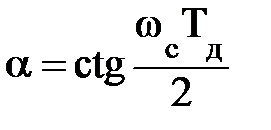 .
.
В результате перехода к нормированным частотам ЦФ Ω = ωТд частотные преобразования (9.15) принимают вид:
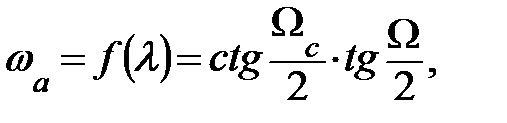 (9.16)
(9.16)
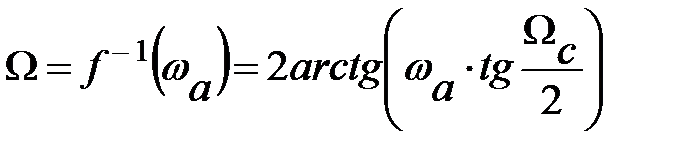
Несмотря на нелинейность частотного преобразования, сжимающего бесконечный диапазон физических частот АФП в основную полосу физических частот ЦФ (0 – 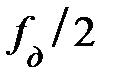 ) (Ω = 0 – π), при синтезе РФ со ступенчатообразными АЧХ обеспечивается необходимая эквивалентность АФП и ЦФ по параметрам ∆n, ∆з, определяющим предельные погрешности аппроксимации, если граничные частоты среза и задерживания их связаны частотной преобразующей функцией:
) (Ω = 0 – π), при синтезе РФ со ступенчатообразными АЧХ обеспечивается необходимая эквивалентность АФП и ЦФ по параметрам ∆n, ∆з, определяющим предельные погрешности аппроксимации, если граничные частоты среза и задерживания их связаны частотной преобразующей функцией:
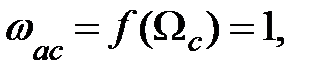
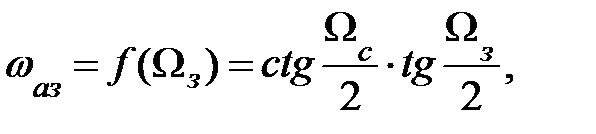
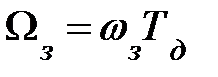
Однако вследствие нелинейности частотного преобразования возможно существенное отличие ФЧХ цифрового и аналогового фильтров.
Синтез аналоговых фильтров с разными типами АЧХ (ФВЧ, ППФ, ПЗФ, МПФ) выполняется по нормализированному аналоговому низкочастотному ФП и он же используется в качестве прототипа при синтезе ЦФ. При этом каждому типу ЦФ ставится в соответствие обобщенное билинейное преобразование p = fоб(z) и соответствующее ему частотное преобразование ωa = fоб(Ω), которые непосредственно устанавливают связь между передаточной функцией и частотной характеристикой АФПНЧ и ЦФ заданного типа и исключают необходимость каких-либо дополнительных промежуточных преобразований.
Для основных типов фильтров обобщенные преобразования приведены в таблице 9.1. Частотные преобразования представлены в таблице соотношениями между граничными частотами аналогового ФНЧ и ЦФ заданного типа. Для цифровых ППФ и ПЗФ в качестве частоты задерживания аналогового ФНЧ – прототипа принимается одна из расчетных частот Ωз1,2 , имеющая наименьшее по модулю значение.
Таблица 9.1
| Тип ЦФ | Преобразование p → z | Преобразование ωa → Ω |
| ФНЧ | 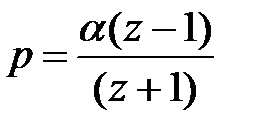
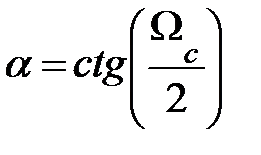
| 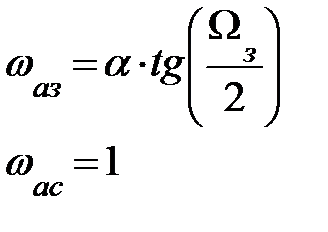
|
| ФВЧ | 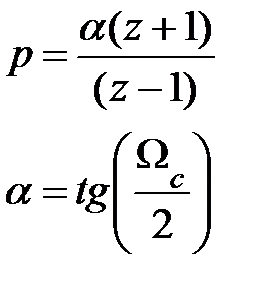
| 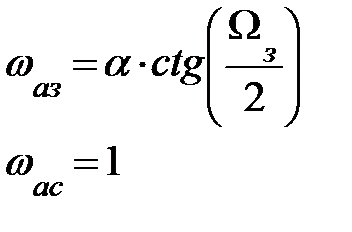
|
| ППФ | 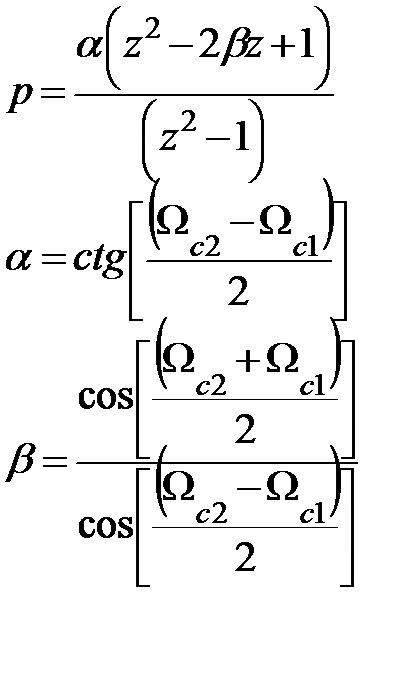
| 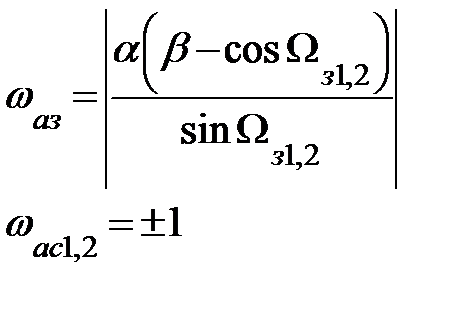
|
| ПЗФ | 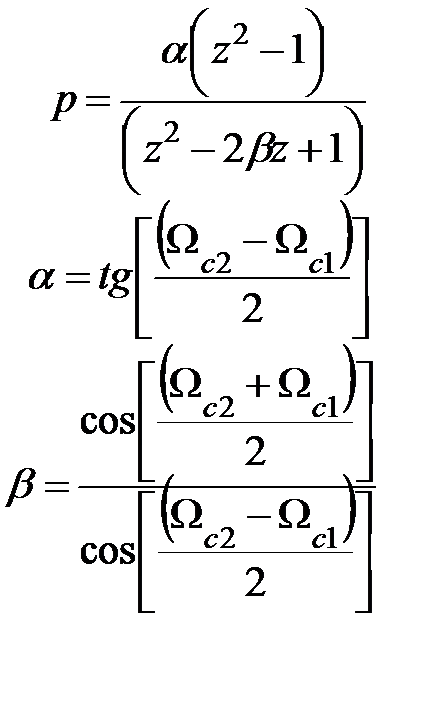
| 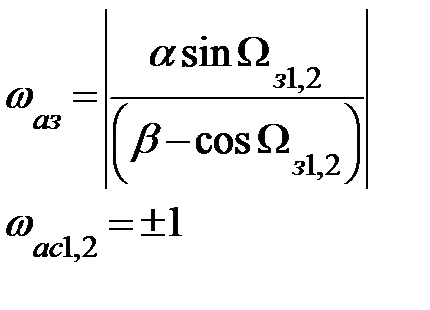
|
Дата добавления: 2017-05-02; просмотров: 2600;











