Рекурсивные цифровые фильтры

Рекурсивный фильтр реализует алгоритмы обработки входного сигнала, описываемый уравнением (9.2). Применяя Z-преобразования к левой и правой части этого уравнения получим:

,

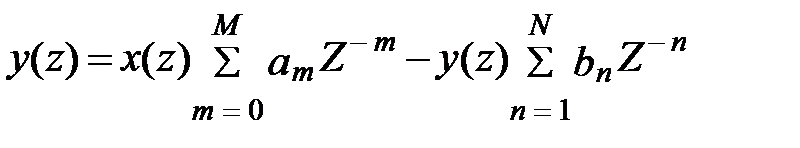Здесь ,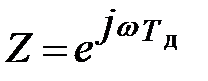

Т_д - период дискретизации.

Передаточной функцией дискретной системы называется отношение Z образов выходного и входного сигналов [1]:

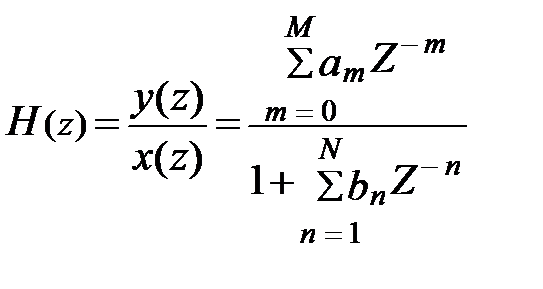(9.5)

Которая представляет собой отношение двух полиномов по степеням комплексной переменной Z^-1 . При этом должно выполняться условие M≤N, которое определяет порядок полиномов и порядок цифрового фильтра (N). Если M > N, уравнение (9.5) преобразуется к сумме двух передаточных функций. Первая – соответствует нерекурсивной передаточной функции (M – N)-го порядка, а вторая – рекурсивной функции, порядок числителя которой всегда меньше N.

По передаточной функции можно легко составить структурную схему дискретной системы, т.е. ЦФ. Передаточную функцию ЦФ (9.5) можно также выразить в виде отношения полиномов A(z) и B(z) по положительным степеням Z, умножив числитель и знаменатель выражения (9.5) на Z^-N . В развернутом виде уравнение передаточной функции ЦФ будет выглядеть так:

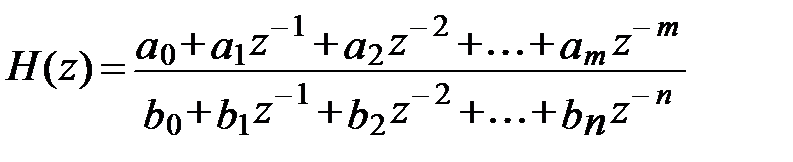, (9.6)

при условии, что M≤N. В этом выражении коэффициенты полиномов a₀ и b₀ играют масштабирующую роль и в общем случае могут быть приравнены к единице.

Передаточная функция в форме (9.6) в точках нулей H(z_oi) = 0, а в точках полюсов H(z_pi) = ∞. Где 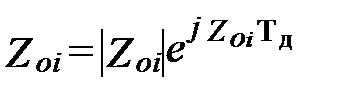, 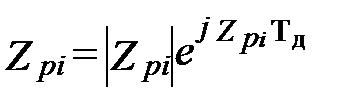- есть нули и полюса функций, а i = 1, 2 … N – есть номер нуля или полюса; N – порядок фильтра. Нули функции передачи могут быть вещественными, либо составлять комплексно-сопряженные пары. То же можно сказать и о полюсах. Коэффициенты полиномов всегда вещественны. Нули и полюса могут быть простыми и кратными.

Если известны нули и полюса передаточной функции, то ее можно представить в виде нуль-полюсной форме, разложив числитель и знаменатель на множители:

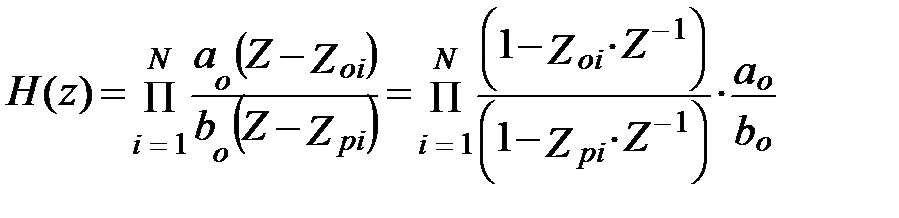(9.7)

Могут присутствовать коэффициенты a₀ и b_0, если они не равны единице.

Выражение передаточной функции (9.6) может быть так же представлено в виде суммы однополюсных или n-полюсных простых дробей [3].

Выражение передаточной функции в форме (9.7) упрощает поиск аналитических выражений импульсных характеристик РФ. Для получения частотной характеристики РФ на основе любого вида передаточной характеристики Н(z) необходимо осуществить замену z = e^jωТд. Например, из выражения (9.5) получим:

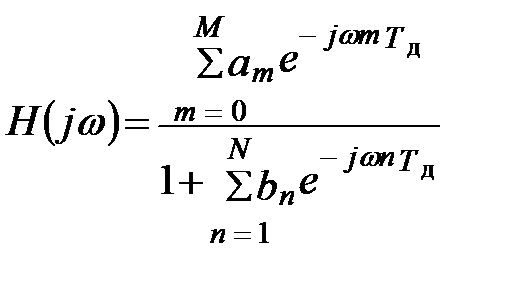, (9.8)

Чему соответствует каноническая форма реализации РФ.

Рис. 9.4 Каноническая форма реализации ЦФ

Из этого же выражения можно найти АЧХ и ФЧХ фильтра, определив модуль и фазу частотной характеристики H(jω).

По расположению нулей и полюсов на комплексной плоскости можно судить об устойчивости РФ. Полюса устойчивого РФ не превышают по модулю единицу (|z_pi|<1) и находятся внутри круга единичного радиуса (для устойчивого аналогового фильтра полюса находятся в левой полуплоскости).

Для расчета АЧХ и ФЧХ РФ используются выражения передаточной функции, соответствующие конкретной форме реализации.