Переход от аналогового фильтра прототипа к цифровому фильтру
С помощью обобщенной преобразующей функции (см. формулу (9.15)) передаточную функцию низкочастотного прототипа можно непосредственно трансформировать в передаточную функцию цифрового фильтра. И далее приводя выражение передаточной функции ЦФ к виду, соответствующему выбранной форме реализации ЦФ, можно найти значения коэффициентов звеньев фильтра a1i, a2i, bоi, b1i, b2i.
Однако такой путь связан с громоздкими математическими преобразованиями, особенно для ППФ и ПЗФ, порядок которых вдвое больше, чем у аналогового прототипа.
Более удобный путь основан на аналитической связи между коэффициентами ЦФ конкретной формы реализации и его нулями и полюсами, которые, в свою очередь, могут быть найдены через полюсы и нули аналогового фильтра прототипа.
Выражение для расчета полюсов и нулей ЦФ через полюсы и нули аналогового фильтра прототипа сведены в таблице 9.2, [1]:
Таблица 9.2
| Тип фильтра | Преобразование | Примечания |
| ФНЧ | 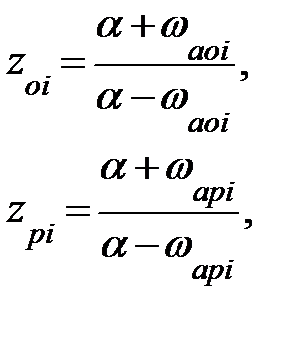 i = 1, 2, …, N. i = 1, 2, …, N.
| При ωaоi = ∞ zоi = -1 |
| ФВЧ | 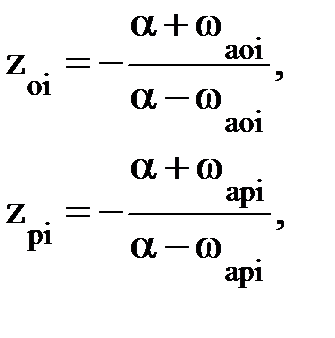 i = 1, 2, …, N. i = 1, 2, …, N.
| Если ωaоi = ∞ zоi = -1 |
| Тип фильтра | Преобразование | Примечания |
| ППФ |
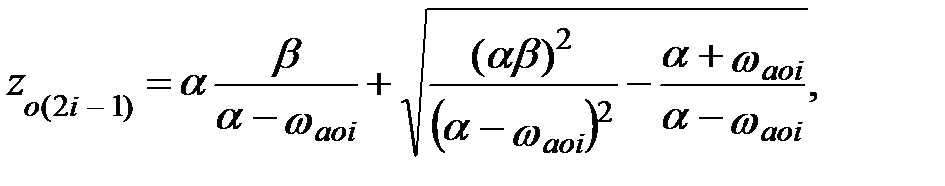
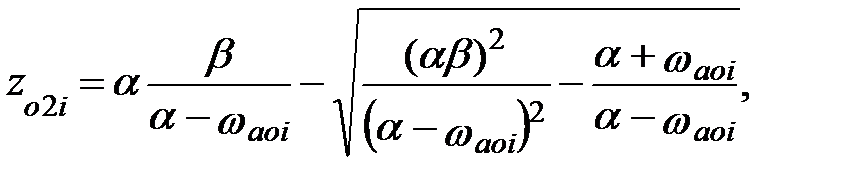
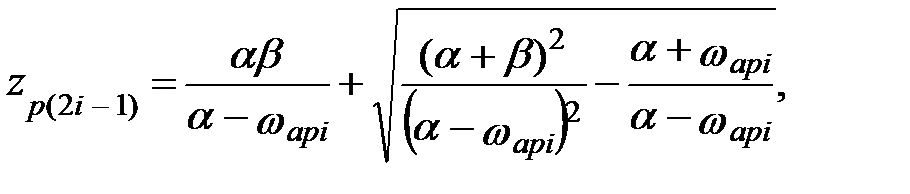
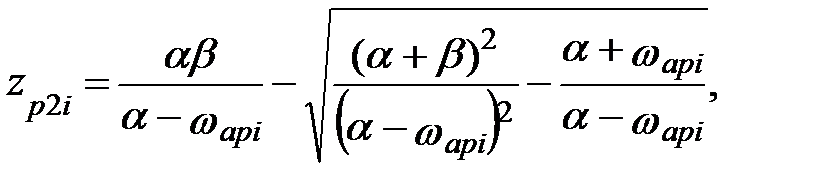 i = 1, 2, …, N.
i = 1, 2, …, N.
| Если ωaоi = ∞ zо, 2i-1 = ±1 zо, 2i = ±1 |
| ПЗФ | 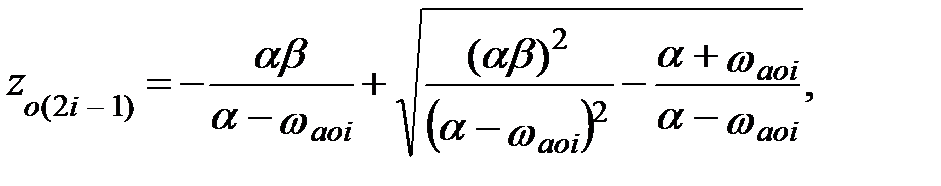
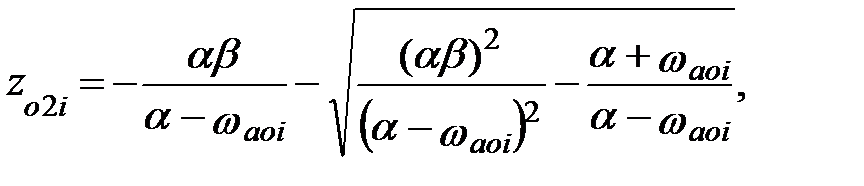
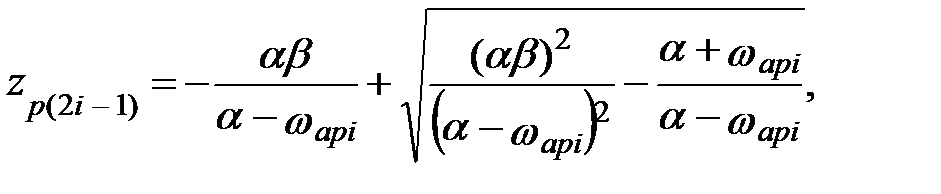
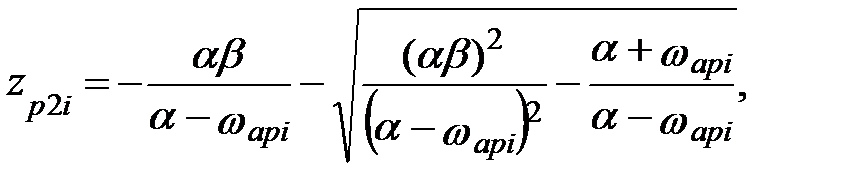 i = 1, 2, …,N.
i = 1, 2, …,N.
| Если ωaоi = ∞
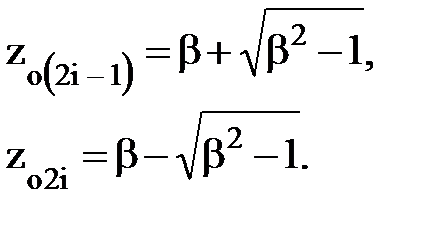
|
Передаточные функции звеньев второго порядка каскадной и параллельной форм реализации получают объединением в пары компексно-сопряженных полюсов фильтра и группированием их в случае каскадной формы с ближайшими по расположению на комплексной плоскости парами нулей.
Число звеньев (L) ЦФ определяется его порядком N: при четном порядке L= 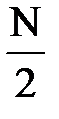 , при нечетном L =
, при нечетном L = 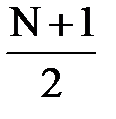 , но при этом одно звено имеет первый порядок и ему соответствуют вещественные значения нуля и полюса.
, но при этом одно звено имеет первый порядок и ему соответствуют вещественные значения нуля и полюса.
Порядок цифровых фильтров ФНЧ и ФВЧ совпадает с порядком аналогового фильтра прототипа, а ППФ и ПЗФ – в два раза больше – 2·N.
Коэффициенты bоi, b1i, b2i, a1i, a2i звеньев находятся через нули и полюсы цифрового фильтра с помощью выражений (9.10 – 9.14), а они определяют передаточную функцию ЦФ для выбранной структуры реализации фильтра.
Дата добавления: 2017-05-02; просмотров: 2119;











