Критерии оптимизации

Важная сторона оптимизации – это выбор критерия, по которому определяются свойства объекта и который позволяет количественно оценить какое из устройств данного класса является наилучшим.

Критерии в зависимости от назначения устройства могут быть самыми разными.

Так при проектировании фильтра критерий может относиться к его амплитудно-частной характеристике, минимуму потерь в полосе прозрачности и максимуму – в полосе заграждения.

В случае усилителя высокочастотных колебаний такой критерий может быть связан с получением максимального КПД, с соблюдением требования по нелинейным искажениям сигнала.

Несмотря на все разнообразие критериев их можно свести к единой математической записи – функции цели, которая в концентрированной форме отражает смысл решаемой задачи по оптимизации устройства – в наилучшем приближении его характеристик к требуемым согласно определенным признакам.

Все действия в такой программе оптимизации в конечном итоге направлены на получение экстремального значения функции цели – максимального или минимального, в зависимости от поставленной задачи.

Поскольку, как правило, качество устройства определяют несколько критериев (например, в приводимом выше примере с фильтром – максимум в одной полосе, минимум – в другой), то целевая функция является суммой определенного числа членов и по своему виду является взвешенно-аддитивно цифровой, отражающей требование минимального отличия желаемых (иногда идеальных) характеристик от реально получаемых. Составим в обобщенном виде функцию цели.

При исследовании в частотной области для целевой функции, определяемой K критериями, запишем:

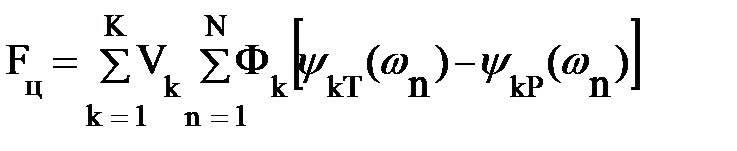(6.5)

где Ф_k – частная целевая функция для k-й характеристики;

ψ_kT – функция, определяющая требуемую k-ю частотную характеристику;

ψ_kP – функция, определяющая реально полученную k-ю частотную характеристику, зависящую от параметров устройства;

V_k – весовой множитель для k-й характеристики.

Мерой расхождения между требуемой и реальной характеристиками могут являться или минимум суммы квадратов уклонений, или минимаксный критерий. При них функция цели примет вид:

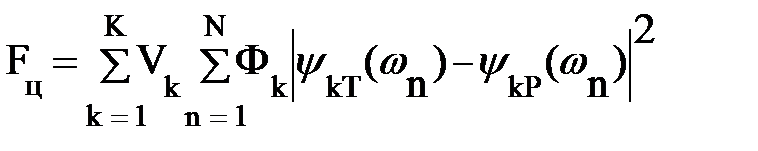(6.6)

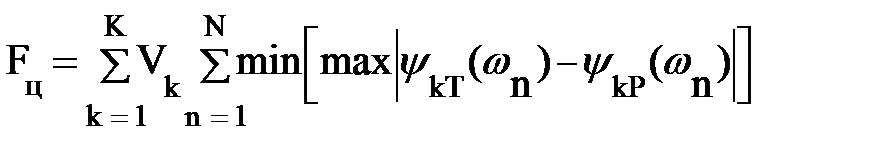(6.7)

Кроме того возможен вариант, когда требуется получить максимальное отношение параметров устройства, например A_k к B_k. Тогда функция цели примет вид:

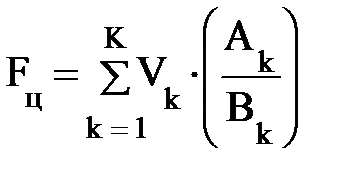(6.8)

Путем определенной процедуры следует найти или минимальное при (6.6) и (6.7), или максимальное при (6.8) значение функции цели. Для определенности рассмотрим первый случай, связанный с получением минимального значения.

Разделим все параметры устройства, определяющие его реальную характеристику ψ_kP, на две группы: варьируемые (x₁,x₂,…,x_n) и неизменные (y₁,y₂,…,y_m). Соберем варьируемые параметры (их еще называют переменными) в вектор-столбец, который затем преобразуем в транспонированную матрицу:

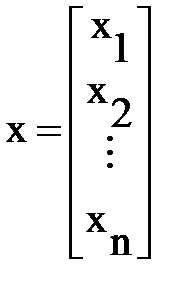
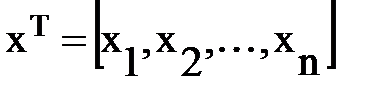(6.9)

Аналогичным образом поступим с постоянными или неизменными параметрами устройства:

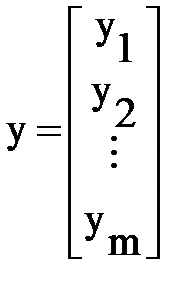
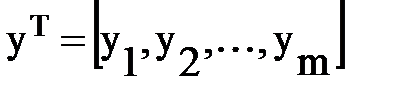(6.10)

Будем рассматривать вектор x как точку или элемент n-мерного действительного пространства Rⁿ . Совокупность объектов x произвольного содержания (точки, векторы, функции и т.д.) составляют множество X, а сами объекты есть элементы этого множества. Совместив понятия точечного множества, составленного из точек х, и n-мерного пространства Rⁿ , можно утверждать, что множество X представляет собой совокупность точек х в многомерном пространстве Rⁿ .

В процессе поиска среди множества векторов x следует найти такой вектор X_опт в пространстве Rⁿ , при котором функция цели (6.6) или (6.7) минимальна:

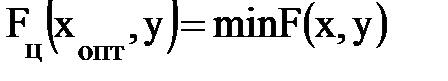_, где x Є Rn (6.11)

При этом на вектор х могут накладываться определенные ограничения. Точка x_опт соответствует наилучшему в соответствии с выбранными критериями варианту проектируемого устройства. Поиск x_опт относится к классу задач, объединяемых теорией нелинейного программирования. При этом вектор х во всех рассматриваемых ниже задачах ограничен определенным пространством Rⁿ , что можно следующим образом представить в развернутом виде:

x_1мин ≤ x₁ ≤ x_1макс, ……….x_n.мин ≤ x_n.макс (6.12)

При функции цели в виде (6.8) выражение (6.11) примет вид:

F_ц (x_опт,y)=maxF(x,y), где x Є Rn (6.13)

Перейдем к рассмотрению путей нахождения x_опт.