Пример записи целевой функции при синтезе фильтров

Проектирование фильтра осуществляется путем процедуры синтеза, включающего два этапа – аппроксимацию и реализацию, исходя из заданных полос пропускания и заграждения, и потерь в них. На первом этапе – аппроксимации – производится замена требуемой характеристики затухания фильтра функцией Чебышева или Баттерворта, либо иной зависимостью отвечающей условиям физической реализуемости. На втором этапе – реализация – определяется структура и параметры элементов фильтра.

Применение компьютера позволило изменить данный подход к синтезу фильтров, имеющих ряд ограничений, и повысить точность расчетов за счет возможности учета ряда факторов.

При компьютерном подходе аппроксимация и реализация заменяются процедурой оптимизации. Производится непосредственный расчет характеристик фильтра на основе определенных рекуррентных соотношений. Осуществляется перебор нескольких типовых структур фильтров и оптимизации параметров в каждом варианте на основе поисковых методов глобального и локального минимума целевой функции.

При таком подходе процедура синтеза представляется как множество вариантов анализа с поиском наилучшего из них согласно определенному критерию. Такая методика предусматривает огромный объем рутинных вычислений, поэтому практическая реализация возможна только с применением компьютера.

При составлении программы параметрического синтеза фильтра функция цели, подлежащая минимизации, может быть представлена в следующем виде:

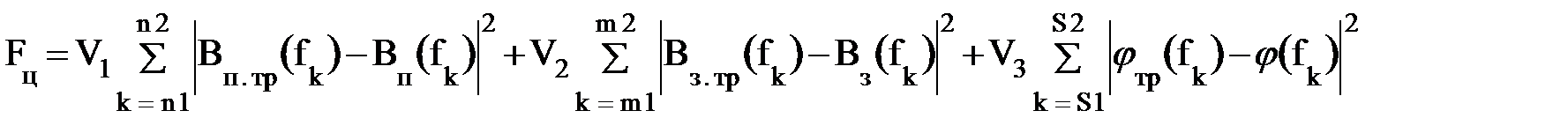
f_n1..f_n2 – полоса пропускания;

f_m1..f_m2 – полоса заграждения;

f_S1..f_S2 – полоса частот фазовой характеристики;

B_п(f_k) – полученное затухание фильтра в полосе пропускания на частоте f_k ;

B_п.тр(f_k) – требуемое затухание фильтра в полосе пропускания;

B_з(f_k) – полученное затухание фильтра в полосе заграждения на частоте f_k ;

B_з.тр(f_k) – требуемое затухание фильтра в полосе заграждения;

φ (f_k) – полученное значение ФЧХ на частоте f = f_k;

φ_тр (f_k) – требуемое значение ФЧХ на той же частоте f = f_k;

V₁, V₂, V₃ – коэффициенты веса, определяющие соотношение требований по затуханию, предъявляющих к полосам пропускания и заграждения, а также другим параметрам.

В качестве примера можно привести задачу минимизации порядка фильтра, обеспечивающего требуемые значения затухания в полосах пропускания и заграждения, а также группового времени запаздывания в полосе пропускания для ФНЧ Баттерворта.

Введем обозначения:

A_min – требуемое затухание фильтра в полосе заграждения;

A_max – требуемое затухание (допустимая неравномерность) фильтра в полосе пропускания;

Ω – текучая частота;

Ω_z – нормированная частота среза (отношение граничной частоты полосы заграждения к граничной частоте полосы пропускания);

Н_Аb(Ω) – амплитудно-частотная характеристика ФНЧ;

L_Аb(Ω) – рабочие затухание ФНЧ;

β_b (Ω) – фазо-частотная характеристика ФНЧ;

τ_b(Ω) – групповое время запаздывания;

Пусть заданы значения:

A_max : ≤ 2; A_min : ≥ 20 ; Ω_z : = 1.6;

Задаем пределы изменения и шаг изменения текущей частоты:

Ω : = 0.2 * Ωz/100 … 2 * Ωz

Wzcp – нормированная частота среза (fгрпн/fв)

Nb – порядок аналогового ФНЧ Баттерворта

Nc – порядок цифрового ФНЧ Чбышева

w – текущая частота

Hb(w) – АЧХ ФНЧ Баттерворта

Нс(w ) – ФЧХ ФНЧ Чебышева

τb(w) – групповое время запаздывания ФНЧ Баттерворта

τс(w) – групповое время запаздывания ФНЧ Чебышева

Amin1 – требуемое рабочее ослабление на частоте среза для фильтра Баттерворта

Amin2 – требуемое рабочее ослабление на частоте среза для фильтра Чебышева

Amax1 и Amax2 – допустимые неравномерности в полосе пропускания фильтров Баттерворта и Чебышева