Пример циклического расчета

Рассчитать с «шагом» 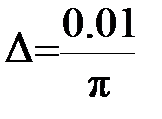затухающий колебательный процесс, описываемый функцией:

,

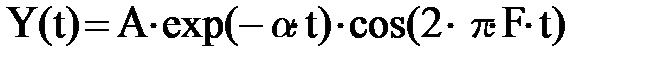при А = 10, α = 0,5, F = 10 и N = 1000.

Организуем цикл расчета с помощью записи k := 0…N и выражений для аргумента t_k и дискретной функции Y_k(t_k), полученной из непрерывной функции Y(t).

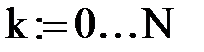
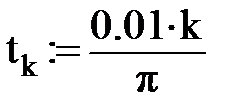
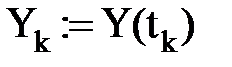
Строим график дискретной функции :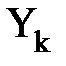

Рис.6.36 График дискретной функции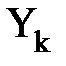

Вывод в виде таблицы дискретных значений 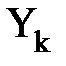осуществляется путем записи Y= или .

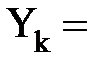По умолчанию на рабочий лист выводится 16 значений функции.

Щелкнув по графику функции, обрамляют ее рамкой и путем протаскивания вниз курсора расширяют таблицу до любого требуемого значения k≤N.

При протаскивании курсора вверх таблица наоборот сжимается.

Таким же образом можно вывести и таблицу значений аргумента, сделав в рассматриваемом случае запись .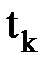

Вопросы для самоконтроля

1. Способы определения корней алгебраических уравнений в среде MathCAD

2. Способы определения корней трансцендентных уравнений в среде MathCAD

3. Способы организации вычислений по циклу

Обработка данных

Обработка данных – это важная сфера применения компьютерной математики.

При решении многих задач в радиотехнике, исходная функция задается в табличной форме или по точкам (например, экспериментально полученные амплитудная или амплитудно-частотная характеристики усилителя). Вместе с тем, для дальнейшего анализа необходимо знать значение функции при любом значении аргумента, а не только при некоторых его конкретных значениях. Данной цели, т.е. к переходу от дискретного описания функции к непрерывному, служит процедура аппроксимации. При определении функции между узловыми точками аппроксимация называется интерполяцией, а за их пределами – экстраполяцией.

«MathCAD» располагает двумя способами интерполяции:

· кусочно-линейной;

· сплайновой (более точная).