ОСНОВНЫЕ ПОНЯТИЯ ТЕРМОДИНАМИКИ. Предмет термодинамики

Техническая термодинамика изучает закономерности взаимного превращения тепловой и механической энергии и свойства тел, участвующих в этих превращениях.

На ее основе осуществляют расчет и проектирование всех тепловых двигателей, а также всевозможного теплотехнического оборудования.

1.2.Термодинамическая система

Термодинамическая система – это совокупность тел, взаимодействующих между собой и с окружающей средой.

Термодинамическая система может обмениваться с окружающей средой энергией, теплом и массой.

Если такой обмен исключен, система называется изолированной, если отсутствует теплообмен – адиабатной, если отсутствует массообмен – закрытой, при наличии массообмена – открытой. Пример закрытой термодинамической системы – газ, заключенный в цилиндре под поршнем, внешняя среда – окружающий воздух. Поток газа или пара в турбине или трубопроводе – открытая термодинамическая система. Газ, находящийся в закрытой емкости с идеальной тепловой изоляцией, и- изолированная и одновременно адиабатная система.

Простейшей термодинамической системой является рабочее тело (газ или пар), с помощью которого в тепловом двигателе осуществляется превращение теплоты в работу. Например, в двигателях внутреннего сгорания рабочим теплом являются продукты сгорания топлива, в паротурбинных установках – водяной пар.

1.3.Термические параметры состояния

Свойства рабочих тел характеризуются параметрами состояния. Термическими параметрами состояния являются: абсолютное давление ρ, абсолютная температура Т, удельный объем υ.

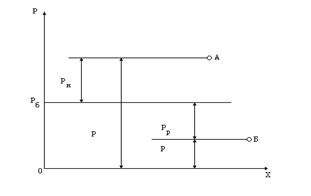
1. Абсолютное давление Р отсчитывается от 0. Избыточное давление (ρ_и) отсчитывается от уровня атмосферного давления и измеряется манометром (жидкостным или пружинным). Атмосферное давление (ρ_б) измеряется барометром. Приборы для измерения давления ниже атмосферного называются вакуумметрами и измеряют разрежение (ρ_р).

Связи между абсолютным давлением ρ и давлениями, измеренными с помощью приборов,

р= р_и+ р_6, (1.1)

р= р₆ - р_р (1.2)

наглядно подтверждаются на . 1.1.

В международной системе единиц (СИ) давление выражается в паскалях (1Па = 1Н/м²). Используются и другие единицы измерения давления (бар, мм рт. ст, ат…):

1 бар = 10⁵ Па = 10²кПа = 0,1 МПа = 750 мм рт. ст.

1 ат = 1 кг/см² = 735,6 мм рт. ст.,

1 физ. атм = 760 мм рт. ст.

2. Абсолютная температура Т измеряется в градусах Кельвина (К)

Т = t+ 273,15,

где t, ^оС – температура в градусах Цельсия, определяемая с помощью термометров, пирометров, термопар и других приборов и устройств.

3. Удельный объем υ – это объем единицы массы вещества υ= V/М, м³/кг, величина, обратная плотности υ= 1/ ρ.

Для сравнения термодинамических систем в одинаковых состояниях вводится понятие «нормальные физические условия»: р= 101,325 кПа (760 мм рт.ст)., Т= 273, 15 К (t=0 ^оС).

1.4 Уравнение состояния

Связь между параметрами р, υ, Т называется термическим уравнением состояния

.

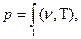
Эти уравнения показывают, что из трех параметров, определяющих состояние системы, независимыми являются два.

Конкретный вид уравнения состояния зависит от свойств веществ.

Для идеального газа термическое уравнение состояния имеет вид:

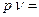RT, (1.3)

MRT, (1.4)

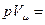R_μT, (1.5)

nR_μT. (1.6)

В уравнениях (1.3) –(1.6) используются следующие обозначения: р – абсолютное давление, Па; υ- удельный объем, м³/кг; Т – абсолютная температура, К; М – масса газа; V – объем газа, м³; V_μ - объем 1 киломоля газа. м³/кмоль; n= М/μ – число киломолей газа; μ- мольная масса газа, кг/кмоль; R_μ = 8314 Дж/кмоль·К) – универсальная газовая постоянная; R=R_μ/μ – газовая постоянная, Дж/кг ·К).

В реальных газах, в отличие от идеальных, существенны силы межмолекулярных взаимодействий, и нельзя пренебречь собственным объемом молекул. Термическое уравнение состояния реального газа можно представить в виде

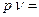zRT, (1.7)

где z= 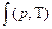- коэффициент сжимаемости.

Вся сложность расчетов по уравнению (1.7) состоит в определении коэффициента сжимаемости. Реальные газы при Т→∞ или р→0 становятся идеальными , при этом z=1.

Понятие идеального газа является научной абстракцией, моделью реального газа, дающей хорошую сходимость с практикой. Для состояний газа, близких к состоянию сжижения (насыщенного пара) модель идеального газа неприемлема.

1.5.Расчет термических параметров газовых смесей

Примерами газовых смесей являются: воздух, природный газ, продукты сгорания топлив и т.д. Ниже рассматривается расчет механических газовых смесей (химически не реагирующих) при условии, что газовая смесь – идеальный газ.

В этом случае:

1. Каждый компонент имеет температуру, равную температуре смеси, и занимает весь объем смеси.

2. Сумма парциальных давлений компонентов равна давлению смеси

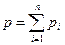(1.8)

3. Сумма парциальных объемов компонентов равна объему смеси

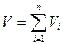(1.9)

Парциальное давление компонента – это давление, которое оказывает компонент на стенки сосуда с газовой смесью.

Парциальный объем компонента – это объем, который бы занимал компонент, имея давления и температуру смеси.

Параметры газовой смеси рассчитываются по уравнению состояния идеального газа, например (1.4)

MRT,

где R=R_μ/μ, μ – мольная масса газовой смеси.

Параметры компонентов рассчитываются по уравнениям:

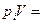M_iR_iT, (1.10)

M_iR_iT, (1.11)

Чтобы воспользоваться этими формулами, необходимо знать мольную массу газовой смеси (μ), парциальные давления (р_i) или парциальные объемы (V_i)_.

Существует три способа задания газовой смеси:

1. По массовому составу.

Масса смеси равна сумме масс компонентов:

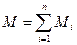, кг

1= 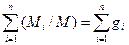, (1.12)

где g_i=M_i/M – массовая доля компонента.

При массовом задании газовой смеси мольная масса рассчитывается по формуле:

μ=1/[ 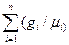] (1.13)

2. По объемному составу.

На основании (1.9)

,

1= 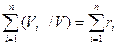, (1.14)

где r_i=V_i/V – объемная доля компонента.

При объемном задании газовой смеси мольная масса рассчитывается по формуле

μ= 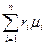, (1.15)

3. По мольному составу.

Согласно закону сохранения массы число киломолей газовой смеси равно сумме киломолей компонентов:

1= 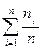(1.16)

где n_i/n мольная доля компонента, численно равная объемной доле r_i

n_i/n=(n_i/n) (V_μ/V_μ) = V_i/V=r_i (1.17)

Здесь V_μ , м³/кмоль – объем одного киломоля газа при параметрах смеси ρ и Т

Таким образом, при мольном задании газовой смеси расчет мольной массы производится по формуле (1.15).

Связь между объемными и массовыми долями характеризуется следующими формулами:

g_i= μ_i ·r_i/μ, (1.18)

r_i = μ·g_i/μ_i (1.19)

На основании уравнений (1.10) и (1.11) получено выражение для вычисления парциальных давлений

p_i= r_i · p (1.20)

1.6 Термодинамический процесс

Термодинамический процесс – это процесс изменения состояния рабочего тела. Например, при перемещении поршня в цилиндре изменяются объем, давление и температура газа, т.е. совершается процесс расширения или сжатия газа. На рисунке 1.2 в ρ-υ- диаграмме представлен термодинамический процесс 1-2 (расширение газа).

Процессы могут быть равновесными или неравновесными, обратимыми и необратимыми.

Равновесным является процесс, при протекании которого в каждый момент времени во всех точках системы (т.е. во всем объеме рабочего тела) одноименные параметры ρ и Т имеют одинаковое значение.

Реальные процессы – неравновесны. Неравновесность может быть уменьшена за счет снижения скорости протекания процесса. В диаграммах можно изобразить только равновесные состояния и процессы.

Обратимым называется равновесный процесс, который можно осуществить в прямом и обратном направлениях через одни и те же промежуточные состояния без дополнительной затраты энергии.

В процессах сжатия и расширения рабочего тела обязательным условием обратимости является отсутствие трения, а в процессах передачи тепла от одного тела к другому таким условием является равенство температур тел, обменивающихся теплом.

Реальные процессы обратимы.

При протекании любого процесса (. 1.3) происходит изменение параметров Δр, Δυ, ΔТ не зависимо от его характера (1-a-2, 1 -d-2, 2-b-1).

Математически это означает, что dv, dp, dT являются полными дифференциалами функций υ=f₁(р, T), р= f₂ (υ,T), T= f₃ (ρ,υ) . Для замкнутого процесса (цикла) 1-a-2-b-1 изменение любого параметра равно нулю:

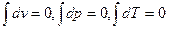
1.7.Методические указания. Вопросы и задачи

1. Обратите внимание на отличия идеального газа от реального. В чем они состоят? При каких условиях реальный газ можно назвать идеальным?

2. Убедитесь, что объем одного киломоля любого газа или газовой смеси зависит только от состояния газа, определяемого двумя независимыми параметрами (р и T, ρ и υ, или Т и υ), но не зависит от свойств газа.

3. Расставьте единицы измерения давления: физ.атм., бар, ат., МПа, кПа в порядке убывания. (Рекомендация: перечисленные размерности следует перевести в мм рт. ст)

4. Цена деления одного градуса на шкале Кельвина и на шкале Цельсия одинакова. Правильно ли это утверждение?

5. Определите, все ли соотношения правильные для рабочего тела, давление которого выше атмосферного:

a) ρ > ρ_и; b) ρ > ρ_б: с) ρ_и ≤ ρ_б; d) ρ_и ≥ ρ_б

6. Определите, все ли соотношения правильные для рабочего тела, давление которого меньше атмосферного:

a) ρ_б > ρ; b) ρ_б > ρ_р: с) ρ_р ≤ ρ; d) ρ_р ≥ ρ

7. Определите массу воздуха, содержащегося в открытой двухлитровой банке при t= 20⁰, р=1 бар. Сравните с массой воды.

Решение

Масса воздуха определяется по уравнению состояния идеального газа (1.4), в которое величины подставляются в строго определенной размерности:

р= 1·10⁵ Па, V= 0,002м³, T= 293 К, R=(8314/29) Дж/(кг К),

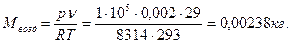
Масса воды в двухлитровой банке при плотности воды ρ= 1000 кг/м³ вычислится по формуле

М _воды= p·V= 1000·0,002=2 кг

Ответы: М _воды=0,00238 кг; М _воды=2 кг.

8. Рассчитайте плотность водорода и азота при нормальных физических условиях, используя уравнение состояния идеального газа. Во сколько раз отличаются их плотности?

9. Объемный расход воздуха при нормальных физических условиях V= 500м³/с. Определите массовый расход воздуха G, кг/с.

10. В смеси 2 кг азота и 0.5кг водорода. Рассчитайте газовую постоянную смеси R.

11. Газовая смесь состоит из двух газов: CO₂ и N₂. Давление смеси ρ= 5 бар, парциальное давление углекислого газа 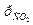= 3 бар. Рассчитайте мольную массу газовой смеси.

Решение

Мольную массу газовой смеси можно рассчитать по формуле (1.15), если предварительно определить объемные доли компонентов по формулам (1.20) и (1.14):

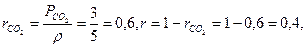
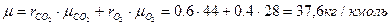
Ответ: = 37,6 кг/кмоль.

12. Состав воздуха по объему: 21% О₂ и 79% N₂. Каков состав воздуха по массе?

13. Какова плотность газовой смеси из СО₂ и N₂ при нормальных физических условиях, если 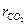=0,3?

1.8. Ответы

3. МПа, физ.атм., бар, ат, кПа. 4.Да. 5.Да. 6.Да. 8. 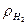= 0,0893 кг/м³, 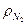= 1,25 кг/м³,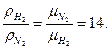 9. G=647,4кг/с. 10. R=1069 Дж/(кг·К).

12. .13.

2. ПЕРВЫЙ ЗАКОН ТЕРМОДИНАМИКИ

2.1. Внутренняя энергия

Внутренняя энергия тела или системы (U, Дж) – это тепловая энергия всех микрочастиц. Она складывается из кинетической энергии микрочастиц(поступательное, вращательное, колебательное движение) и потенциальной энергии (межмолекулярное взаимодействие).

Удельная внутренняя энергия u=U /М, Дж/кг является параметром состояния:

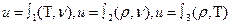
Внутренняя энергия идеального газа определяется только кинематической энергией микрочастиц, поэтому зависит только от температуры u= .

2.2 Работа изменения объема

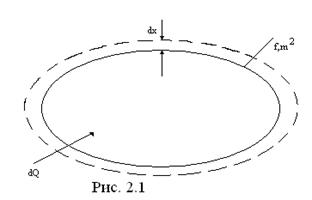Известно, что при нагревании газы расширяются и совершают работу.

Пусть газ массой M, объемом V заключен (.2.1) в эластичную оболочку с поверхностью ∫ и находится под давлением ρ. При проводе к газу теплоты dQ он расширится (каждая точка оболочки переместится на расстояние dx ) и совершит работу dW=ρ∫dx, Дж. Поскольку ∫·dx=dV, м³, то dW=ρdV.

Для 1 кг газа

,

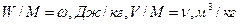dω=ρdυ, (2.1)

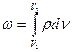. (2.2)

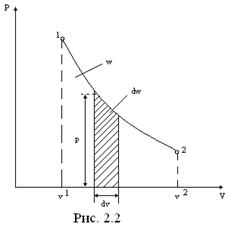Работа изменения объема ( ) произвольного процесса 1-2 в ρ–υ-диаграмме характеризуется площадью υ₁-1-2- υ₂ (рис.2.2).

Работа зависит от характера процесса. Работа положительна (dω>0), если объем рабочего тела увеличивается (d >0), и наоборот.

Работа изменения объема (ω) является характетикой закрытых систем. Для потока рабочего тела (открытая термодинамическая система) рассчитывают внешнюю работу.

2.3. Внешняя работа

Примером открытой термодинамической системы является компрессор, сжимающий воздух.

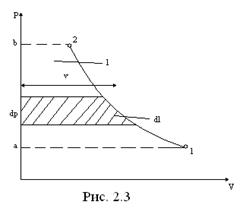На рис. 2.3 в ρ–υ-диаграмме показаны процессы, сопровождающие его работу. Воздух, забираемый из окружающей среды, заполняет цилиндр (a-1), сжимается (1-2) и выталкивается к потребителю (2-b).

Внешняя работа процесса сжатия 1-2 равна:

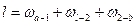(2.3)

Вычисляя слагаемые в правой части (2.3), имеем:

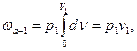
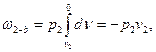
Подстановка их в (2.3) дает следующие выражения для расчета внешней работы:

l = p₂v₁ + w – p₂v₂ (2.4)

l = w – (p₂v₂ – p₁v₁) (2.5)

которые характеризуют связь между внешней работой и работой изменения объема в любом процессе.

Использование дифференциальной записи уравнения (2.5)

dl = dw – d(pv) = dw – pdv - vdp = -vdp

Позволяет получить важные формулы для внешней работы:

dl = - vdp (2.6)

l = - vdp (2.7)

В диаграмме ρ–υ внешняя работа любого процесса изображается (2.3) площадью -1-2. Согласно (2.6) работа положительна (0). Если давление уменьшается (0). И наоборот. Внешняя работа () так же, как и работа, зависит от характера процесса, следовательно, является функцией процесса (в отличие от параметров, которые являются функцией состояния).

2.4 Математическое выражение первого закона термодинамики

Вся подводимая к рабочему телу теплота расходуется на изменение внутренней энергии и на совершение работы:

Q=U₂-U₁+W, Дж (2.8)

q=u₂-u₁+ω, Дж/кг (2.9)

q=Δu+ω, (2.10)

dq=du+dω, (2.11)

dq=du+pdυ (2.12)

Формулы (2.8) и (2.12) математически выражают первый закон термодинамики через внутреннюю энергию.

Постановка ω=l-p₁υ₁+ p₂υ₂ в (2.9) дает,

q=(u₂+p₂υ₂)-(u₁+p₁υ₁)+l,

где u+pυ=h, Дж/кг - удельная энтальпия, является параметром состояния

Энтальпия идеального газа зависит только от температуры

При количественном анализе процессов часто используется математическая запись первого закона термодинамики через энтальпию:

Q=H₂-H₁+L, Дж (2.13)

q=h₂-h₁+l, Дж/кг (2.14)

q=Δh+l (2.15)

dq=dh+dl (2.16)

dq=dh-υdp. (2.17)

2.5. Теплоемкость газов

Теплоемкость – это количество тепла, которое необходимо подвести к единице количества вещества, чтобы нагреть его на 1^о.

Различают теплоемкости:

-массовую (с, Дж/кг·К), отнесенную к одному килограмму газа;

-объемную (с^/, Дж/м³·К), отнесенную к одному м³ объема при нормальных физических условиях;

-мольную (μс, Дж/(кмоль·К)), отнесенную к 1 киломолю газа,

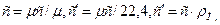
Где - плотность газа при нормальных физических условиях (ρ=760 мм рт. ст.,t = 0 ^оС).

Согласно определению теплоемкости

c=dq/dt, (2.18)

dq=cdt, (2.19)

q= 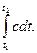(2.20)

Теплоемкость реальных газов зависит от давления и от температуры c=∫ (p,T).

Теплоемкость идеальных газов (кроме одноатомного) зависит только от температуры с=∫ (T).

Теплоемкость одноатомного идеального газа постоянна (c=const)

Для газов, теплоемкость которых зависит от температуры, различают истинную и среднюю теплоемкость. Формула (2.18) определяет теплоемкость при данной температуре – истинную теплоемкость.

На . 2.4 показана зависимость теплоемкости газа от температуры (1-2).

Исходя из геометрического смысла интеграла, можно записать:

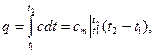
где – средняя теплоемкость газа для интервала температур 1-2, которая может быть вычислена по одной из формул:

(2.21)

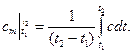(2.22)

Среднюю теплоемкость 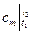можно рассчитать:

-по результатам эксперимента, используя формулу (2.21);

- по формуле (2.22), используя зависимость теплоемкости от температуры, например,

c=f+bt или c=a+bt+dt²

где a,b,d– постоянные величины;

- через средние теплоемкости

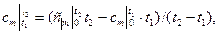(2.23)

Для воздуха таблица средних теплоемкостей и т.д. дана в Приложении.

Изменение температуры газа при одном и том же количестве сообщаемой теплоты зависит от характера процесса подвода теплоты, поэтому теплоемкость является функцией процесса:

- в изобарных процессах – изобарная теплоемкость ;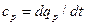

- в изохорных – изохорная ;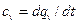

- в изотермических c = dq/0 = ∞;

- в адиабатных c= 0/dt = 0;

- в политропных .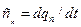

Связь изохорной и изобарной теплоемкостей для идеального газа описывает уравнение Майера

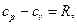(2.24)

(2.25)

Отношение теплоемкостей 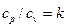называется показателем адиабаты или коэффициентом Пуассона.

Для идеального газа

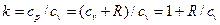
Отсюда

c_v = R/(k-1) (2.26)

c_p = kR/(k-1) (2.27)

Молекулярно-кинетическая теория теплоемкости, основанная на допущении о равномерном распределении энергии по степеням свободы молекул и не учитывающая энергию внутримолекулярных колебаний, дает следующие значения мольных теплоемкостей:

- для одноатомных газов кДж/(кмоль·К);

- для двухатомных газов 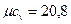кДж/(кмоль·К);

- для трех- и многоатомных газов 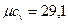кДж/(кмоль·К).

В одноатомных газах отсутствуют внутримолекулярные колебания и постоянное значение теплоемкости, не зависящее от температуры 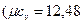кДж/(кмоль·К)), подтверждается экспериментальными данными. Теплоемкости остальных газов зависят от температуры, и указанные значения теплоемкости подтверждаются экспериментальными данными только в области комнатных температур.

Энергию колебательного движения атомов в молекуле учитывает квантовая теория теплоемкости. Значения теплоемкостей для двух-, трех- и многоатомных газов, рассчитанные по формуле Эйнштейна, подтверждаются экспериментом и приводятся в справочниках.

Теплоемкость газовой смеси рассчитывается по формулам:

, Дж/(кг·К), (2.28)

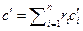, Дж/(м³·К) (2.29)

, Дж/(кмоль·К). (2.30)

2.6. Методические указания.

1. Обратите внимание на следующее:

а) параметры

- это функция состояния, и их изменение ( 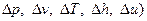не зависит от характера процесса;

б) работа (l,w), теплоемкость (c) являются функциями процесса и зависят от характера процесса;

в) энтальпия, внутренняя энергия, теплоемкость идеального газа зависят только от температуры:

г) теплоемкость одноатомного идеального газа не зависит от температуры (c=const).

2. Уясните физический смысл внутренней внутренней энергии (u) и энтальпии (h) рабочего тела, работы изменения объема (w) и внешней работы (l).

3. Можно ли утверждать, что математическое выражение первого закона термодинамики через внутреннюю энергию справедливо для закрытых термодинамических систем, а через энтальпию – для открытых?

4. Давление газа в изохорном v=0,5м³/кг p₁=6бар до p₂=1 бар

Определите работу изменения объема (w) и внешнюю работу (l) указанного процесса. Представьте процесс в ρ–v-диаграме и покажите соответствующим этим работам площади.

5. Для изотермического процесса идеального газа дано: p=a/v, где a =const; p₁=10 бар; v₁=0,5м³/кг, p₂=1 бар.

Определите внешнюю работу (l), изменение энтальпии (Δh), теплоту процесса (q).

Решение

Внешняя работа изотермического процесса, согласно (2.7) и уравнению p=a/v, равна

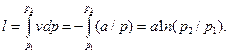
Постоянная a=p₁v₁=10·10²·0,5=500, кПа·м³/кг

l=500 ln (10/1)=1151,3 кДж/кг

Изменение энтальпии идеального газа в изотермическом процессе Δh=0. Теплота изотермического процесса q=l согласно (2.15)

Ответы: l=q =1151,3 кДж/кг Δh =0

6. Температура воздуха увеличилась от t₁=30 ^оC до t₂=150 ^оС

Определите, на сколько изменение энтальпии (Δh) воздуха отличается от изменения внутренней энергии (Δu). Принять, что воздух – идеальный газ.

7. Рассчитайте изохорную и изобарную теплоемкости гелия, отнесенные к одному килограмму газа. Мольная масса гелия μ=4кг/кмоль.

8. Определите среднюю мольную изобарную теплоемкость водорода в интервале температур 400-600 ^оС, если истинная теплоемкость описывается формулой

μc_p=28,7395 + 0,005862 , кДж/(кмоль· ^оС).

9. Определите массовую теплоемкость (c_p)генераторного газа, если его объемный состав r_H2=0,18, r_CO=0,24, r_CO2=0,006, r_N2=0,52.

Примечание. Теплоемкость компонентов принять постоянной согласно молекулярно-кинетической теории газов.

Решение

В соответствии с молекулярно-кинетической теорией газов молная изохорная теплоемкость углекислого газа (CO₂) μc_v=29,1кДж/(кмоль·К), двухатомных газов (H₂, СО, N₂) = μc_v=20,8 кДж/(кмоль·К),.

Мольные изобарные теплоемкости согласно (2.25) для двухатомных газов:

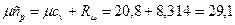кДж/(кмоль ·К),

для СО₂

μc_p=29,1+8,314=37,4 кДж/(кмоль·К).

Согласно (2.30) мольная изобарная теплоемкость газовой смеси

=29,1·0,18+29,1·0,24+29,1·0,52+37,4·0,06=29,6 кДж/(кмоль·К)

Согласно (1.15) мольная масса генераторного газа

=2·0,18+28·0,24+28·0.52+44·0,06=24,28 кг/кмоль.

Массовая изобарная теплоемкость генераторного газа

c_p==μc_p/μ=29,6/24,28=1,219 кДж/(кгК).

Ответ: с_p=1,219 кДж/кг·К).

10. Рассчитайте среднюю изобарную теплоемкость воздуха, отнесенную 1 кг, в интервале температур 700-900 ^оС, используя табличные значения теплоемкосте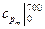й и 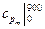(см. Приложение).

2.7 Ответы

3. Да. 4. l=250 кДж/кг, w=0. 6. Δh-Δu=R (T₂-T₁)=34,4 кДж/кг.

7. c_v=3,12 кДж/(кг·К), c_р=5,2 кДж /(кг·К).

8. μc_pm=31,67 кДж/(кмоль·К). 10. c_pm=1,154 кДж/(кг·К).

3. ВТОРОЙ ЗАКОН ТЕРМОДИНАМИКИ

4.

3.1. Формулировки и математическое выражение второго закона термодинамики

Формулировка Клазиуса. Теплота не может сама собой переходить от холодного тела к горячему.

Формулировка Больцмана. Все естественные процессы являются переходом от менее вероятного состояния к более вероятному.

Формулировка Карно. Для превращения теплоты в работу необходимо иметь два источника теплоты разной температуры (. 3.1.)

Горячим источником в тепловых двигателях является топливо (органическое или ядерное), солнечная энергия, геотермальная энергия и т.д., холодным источником – окружающая среда.

Здесь q₁ – теплота, подводимая от горячего источника к рабочему телу в тепловом двигателе; q₂ – отводимая теплота от рабочего тела; l- работа, полученная в тепловом двигателе.

Одна из формулировок второго закона термодинамики гласит: вечный двигатель второго рода невозможен. Это двигатель, который бы работал без холодного источника и всю подводимую теплоту (q₁) преобразовывал в работу.

Таким образом, работа, полностью превращается в теплоту, в то время как теплота превращается в работу – только частично.

Математическое выражение второго закона термодинамики для обратимых процессов имеет вид:

dq = Tds, (3.1)

q = 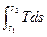(3.2)

де q – подводимая (извне) или отводимая от рабочего тела теплота;

s, Дж /(кгК) – удельная энтропия, являющаяся параметром состояния

s= f₁ (p,T); s= f₂ (v,T); s= f₃ (p,v).

На основании (3.1) можно сделать следующие выводы:

1. При подводе тепла к рабочему телу (dq>0) энтропия возрастает (ds>0).

2. При отводе тепла от рабочего стола (dq<0) энтропия убывает (ds<0).

3. В адиабатных процессах и системах (dq=0) энтропия не изменяется (ds=0,s =const).

4. В изотермических процессах выполняется равенство

q= T (s₁-s₂)=TΔs.

Математическое выражение второго закона термодинамики для необратимых процессов dq <Tds, (3.3)

q< 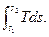(3.4)

Трение и неравновесность реальных процессов сжатия и расширения относят к внутренней необратимости. Необратимый теплообмен между телами при конечной разности температур называется внешней необратимостью.

Как внутренняя, так и внешняя необратимости сопровождаются увеличением энтропии (), что и учитывается уравнениями (3.3) и (3.4).

3.2. T-s-диаграмма

На . 3.2 в – T-s- диаграмме показан произвольный процесс 1-2.

Согласно уравнениям (3.12) и (3.2) площадь под кривой (s₁-1-2-s₂) характеризует теплоту этого процесса.

Теплота подводится (dq > 0), если энтропия увеличивается (dq > 0, s₂ > s₁). Теплота отводится (dq<0), если энтропия уменьшается (ds < 0, s₂ < s₁). Теплота (q), как и работа (w, l), является функцией процесса, зависит от его характера.

3.3. Круговые процессы (циклы)

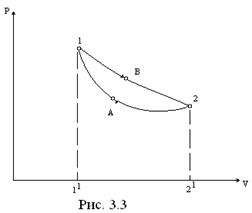
В тепловом двигателе рабочее тело совершает замкнутый процесс (цикл) в направлении движения часовой стрелки (. 3.3 и 3.4).

На участке 1-В-2 (. 3.3) происходит расширение рабочего тела, на участке 2-А-1 – его сжатие.

Работа процесса расширения (полученная работа) равна

w_1-B-2= 1-B-2-2¹-1¹

работа процесса сжатия (затраченная работа) равна

w_2-А-1= 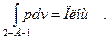2-А-1-1¹-2¹

результирующая (полезная) работа равна

l= w_1-B-2 – w _2-F-1= =Площ. 1-B-2-A

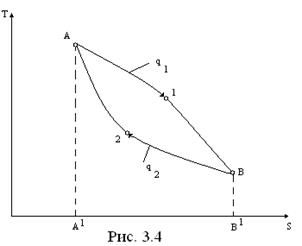
На участке А-1-В (. 3.4) осуществляется процесс подвода теплоты к рабочему телу, а на участке В-2-А – ее отвод.

Подведенная теплота в цикле равна

q₁= = Площ. А-1-В-В′-А′,

отведенная теплота равна

q₂= 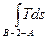= Площ. В-2-А-А′-В′,

Разность подведенной и отведенной теплот превращается в работу

l=q₁-q₂=…….Tds= Площ. А-1-В-2,

и она характеризуется площадью цикла в T-s- диаграмме.

Таким образом, p-v и T-s–диаграммах площадь цикла является работой теплового двигателя.

Такой же результат получается с использованием математического выражения первого закона термодинамики для замкнутого процесса (цикла). Выполняя игтегрирование по замкнутому контуру, имеем

…..Tds= ….du + …pdv.

Поскольку ….du=0, следовательно,

…Tds = ….pdv = l.

3.3.1. Цикл Карно

Термическим коэффициентом полезного действия (КПД) цикла называется отношение работы. Произведенной двигателем за цикл, к количеству теплоты, подведенной за этот же цикл:

Термический КПД характеризует степень термодинамического совершенаства обратимых циклов.

Цикл Карно – это обратимый цикл, который имеет максимальный термический КПД среди всех циклов. Осуществляемых в данном интервале температур горячего и холодного источников тепла. Он состоит из двух адиабатных процессов сжатия и расширения рабочего тела (da и bc, . 3.5) и двух изотермических процессов подвода и отвода теплоты (аb и cd).

Подводимая теплота в цикле

q₁=T₁ (s₂-s₁), (3.6)

отводимая теплота

q₂=T₂ (s₂-s₁), (3.7)

где 1 – температура горячего источника, 2 – температура холодного источника.

Согласно (3.5), (3.6) и (3.7) термический КПД цикла Карно равен

(3.8)

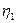он не зависит от свойств рабочего тела, а определяется только температурами горячего и холодного источников тепла. Поскольку Т₂ > 0 и Т₁ < , то < 1.

3.4. Понятия средних термодинамических температур подвода и отвода тепла

На . 3.6 представлен произвольный обратимый цикл 1-a-2-b в T-s- диаграмме.

Подводимая теплота в цикле (q₁) характеризуется площадью с-1-a-2-d и может быть заменена площадью равновеликого прямоугольника с-3-4-d. Таким образом

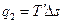(3.9)

где 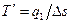- средняя термодинамическая температура подвода теплоты в произвольном обратимом цикле.

Аналогично отводимая теплота равна

(3.10)

где 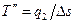- средняя термодинамическая температура отвода теплоты.

Подстановка (3.9) и (3.10) в (3.5) дает

(3.11)

Таким образом, термический КПД произвольного обратимого цикла всегда может быть вычислен через средние термодинамические температуры подвода и отвода теплоты. Из формулы (3.11) следует: чем выше T′, или чем ниже Т′′, тем больше термический КПД цикла.

3.5. Эксергия теплоты

Эксергией теплоты, переданной от горячего источника тепла с температурой Т к рабочему телу называется максимальная работа, которая может быть получена за счет этой теплоты при условии, что холодным источником является окружающая среда с температурой Т_ос.

Максимальную работу ( 3.7) можно получить . если осуществить цикл Карно (1-2-3-4) в данном интервале температур Т-Т_ос.

Теплота, воспринятая рабочим телом от горячего источника, равна

q = TΔs = Площ. с-2-3-d

Эксергия теплоты вычисляется следующим образом:

ex_q = l = q-T_ocΔs = Площ. 1-2-3-4,

exq = q-TocΔs (3.12)

где Т_осΔs – энергия, непревратимая в работу часть теплоты.

Термический КПД цикла Карно равен

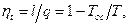
откуда

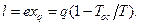(3.13)

Таким образом, эксергия теплоты, полученной от источника теплоты с постоянной температурой Т, может быть рассчитана по формулам (3.12) и (3.13).

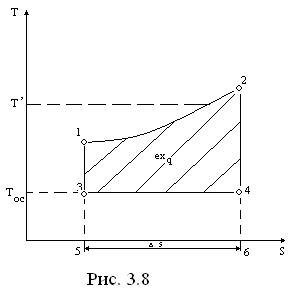В том случае, когда источник теплоты имеет переменную температуру (. 3.8) (например, горение топлива происходит при постоянном давлении с увеличением 7), применимы формулы (3.12) и (3.14).

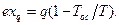(3.14)

где Т′= q/Δs – средняя термодинамическая температура подвода теплоты в процессе 1-2.

При передаче теплоты от тела с более высокой температурой к телу с более низкой температурой (внешний необратимый процесс) эксергия теплоты уменьшается.

Пусть (. 3.9) теплота q передается от тела с температурой T₁ к телу с температурой Т₂. Переданная теплота характеризуется одинаковыми площадями в T-s-диаграмме:

q= Площ. 1-2-3-4=Площ. 1-5-6-7. Эксергия теплоты уменьшилась (Площ. m-5-6-9<Площ. m-2-3-8) на величину потерянной эксергии (Площ. 4-8-9-7).

Таким образом, потеря эксергии составляет

Δex_nom =T_oc ΔS_H (3.15)

где ΔS_H – увеличение энтропии от необратимости процесса теплообмена.

Уравнение (3.15), которое называют уравнением Гюи – Стодолы, имеет важное значение, к. характеризует потерю эксергии любых необратимых процессов.