Причины ослабления импульсных оптических сигналов в процессе их распространения по стекловолокнам

Материальная дисперсия представляет собой зависимость абсолютного показателя преломления диэлектрика (СВ) от частоты света, воздействующего на этот диэлектрик

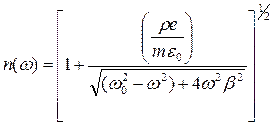, (3.48)

где n = АПП СВ; w – циклическая частота света; r – объемная плотность связанных зарядов в структуре СВ; m – масса электрона; e₀ – электрическая постоянная; w₀ – собственная частота колебаний валентного электрона в узле структуры СВ; b – коэффициент затухания вынужденных колебаний валентного электрона под воздействием света.

График зависимости (3.48) показан на рисунке 3.22.

Участки АВ и CD на рисунке 3.22 называются областями нормальной дисперсии, где ( 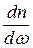) > 0. BC – область аномальной дисперсии, где ( 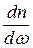) < 0.

В окрестности резонансной частоты 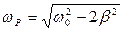, располагающейся внутри интервала ВС, амплитуда смещения X₀ центра масс валентного электрона резко возрастает за счет резонансного поглощения этим электроном световой энергии, и диапазон СВ становится непрозрачным для стекловолокна в области аномальной дисперсии.

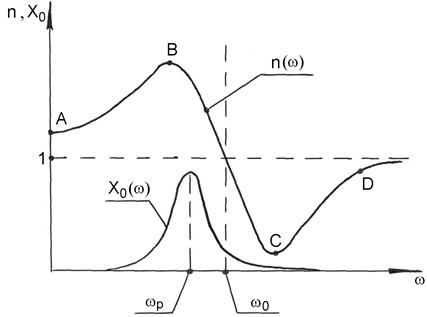
Рисунок 3.22 – Материальная дисперсия: n(w) – зависимость АПП от циклической частоты волны; X₀(w) – зависимость амплитуды смещения центра масс валентного электрона стекловолокна от w, при резонансе

Во всех реальных стеклах, используемых для изготовления стекловолокон, число валентных электронов в узлах структуры больше единицы и кривая дисперсии n(w) имеет более сложную зависимость определяемую формулой 3.49 и рисунком 3.23

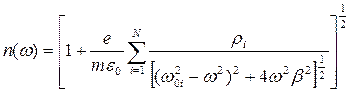(3.49)

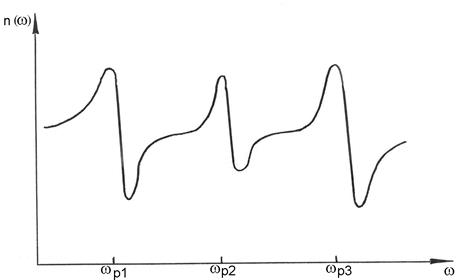
Рисунок 2.23 – Резонансное поглощение световой энергии валентными электронами структуры стекловолокна вблизи частот wр₁, wр₂, wр₃

В заключение данного раздела заметим, что в процессе изготовления СВ в исходную SiO₂ вводятся примеси повышающие АПП = n_С, (ZrO₂, TiO₂, Al₂O₃, GeO₂, P₂O₅) и понижающая АПП = n₀ (B₂O₃, F). Каждая из введенных примесей имеет свои валентные электроны в центральной части волокна и число областей резонансного поглощение света увеличивается по сравнению с рисунком 3.23.

Потери, связанные с рэлеевским рассеянием света в стекловолокне. В стекле, при любой температуре Т ¹ 0, присутствуют фононы – тепловые колебания ионов в узлах структуры. Наличие фононов приводят к незначительным изменениям механической плотности r на величину Dr. Изменения Dr вызывают изменения АПП на величину Dn. Величина Dn пропорциональна амплитуде X₀ смещения ионов в узлах структуры стекла. Согласно экспериментальным данным, X₀ << l, где l - длина световой волны в стекле.

В разделе 3.12 было показано, что любое изменение АПП приводит к рефракции света. В рассматриваемом случае изменение Dn за счет фононов происходит беспорядочно, случайно. Следовательно, беспорядочна и микрорефракция света. Такую рефракцию называют рэлеевским рассеянием. Рэлеем было показано, что взаимосвязь интенсивности рассеянного света I_VP с интенсивностью нерассеянного света I₀ может быть представлена в виде

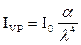, (3.50)

где a – коэффициент пропорциональности, зависящий от типа структуры стекла, типа связей между ионами, наличия примесей, температуры.

Анализ формулы (3.50) показывает, что использование СВ на длинах волн l < 0,85 мкм в магистральных трактах волоконно-оптических линий связи (ВОЛС) практически исключено в настоящее время и допустимо для l ³ 0,85 мкм.

Потери, обусловленные наличием гидроксильных групп ОН, в стекловолокнах. К особо опасным примесям следует отнести гидроксильную группу (ОН), которая способна внедряться в СВ в процессе его роста как из расплава, так и из газовой фазы. Группа (ОН) образуется из паров H₂O, которые всегда находятся в воздухе. При высоких температурах роста СВ, молекула H₂O теряет один ион водорода и превращается в гидроксильную группу. Группа (ОН), внедряясь в СВ, обладает собственными частотами поглощения, соответствующими длинам волн (1,39 – 1,24 – 1,13 – 0,95 – 0,88 – 0,72) мкм. Группы (ОН) способны вызывать поглощения света в СВ до 1ДБ/км и более. Способы борьбы с гидроксильными группами (ОН) очевидны: совершенствования чистоты технологии производства СВ.

Совместное влияние материальной дисперсии, рэлеевского рассеяния и примесей на затухание импульсных сигналов в стекловолокнах. Анализ потерь, рассмотренных в разделах 3.16.1 ¸ 3.16.3 показывает, что собственные резонансные частоты SiO₂, примесей и гидроксильных групп (ОН) оставляют для СВ лишь несколько “окон” прозрачности, при их использовании в магистральных трактах ВОЛС. Типичными из них являются длины волн в окрестности 0,85 мкм, 1,3 мкм, 1,55 мкм, показанные на рисунке 3.24, где К(l) – коэффициент суммарных потерь в условных единицах, l - длина волны.

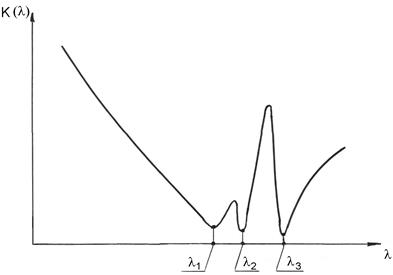
Рисунок 3.24 – «Окна» прозрачности в СВ на основе SiO₂, легированного примесями : l₁ = 0,85 мкм, l₂ = 1,31 мкм, l₃ = 1,55 мкм

Комбинационное рассеяние света. В 1928 г. Раманом и независимо Ландсбергом был открыт эффект возникновения излучения света с частотами u₀ – Du, u₀ + Du, при условии введения в диэлектрик излучения с частотой u₀ и отсутствии какого - либо другого внешнего воздействия.

Поскольку, в результате указанного явления, в диэлектрике вместо волны с частотой u₀ оказались три волны с частотами u₀, u₀ – Du, u₀ + Du, открытый авторами эффект получил название комбинационного рассеяния света. Природа комбинационного рассеяния заключается в фотон – фононном воздействии. Максимальная энергия фонона в твердом теле (и, в том числе, в СВ) определяется выражением

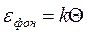, (3.51)

где k – постоянная Больцмана;

Q – характеристическая температура Дэбая;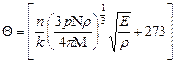

h – постоянная Планка;

p - число ионов, образующих устойчивую связь (в SiO₂, p = 3);

М - масса киломоля диэлектрика (в SiO₂, M = 60 );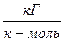

r - плотность диэлектрика;

Е_Ю – модуль Юнга;

N_А = 6,022×10²⁶ 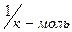– число Авогардо.

По закону сохранения энергии и согласно (2.51) 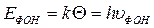, откуда максимальное изменение частоты фотона, при комбинационном рассеянии

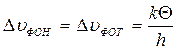. (3.52)

Очевидно, что при комбинационном рассеянии света, максимальна частота фотонов

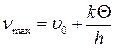, (3.53)

а минимальная

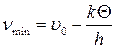. (3.54)

Оптическое излучение с частотами типа (3.53) получило название «фиолетовых» спутников (относительно u₀), излучение типа (3.54) называют «красными» спутниками. Очевидно, что комбинированное рассеяние ослабляет основной сигнал частоты u₀ и ухудшает монохроматичность излучения. Потери за счет комбинационного рассеяния значительно меньше потерь за счет рэлеевского рассеяния и материальной дисперсии.

Вынужденное комбинационное рассеяние. Процесс вынужденного комбинационного рассеяния (ВКР) света относится к классу нелинейно-оптических эффектов, в которых мощная световая волна индуцирует элементарные возбуждения в среде (оптические и акустические фононы, поляритоны, температурные волны и т.п.) и конкретным образом рассеивается на них. При ВКР речь идет о когерентном возбуждении оптических фотонов. Данный процесс есть вынужденный аналог спонтанного комбинационного рассеяния (СКР), при котором свет рассеивается на хаотических тепловых колебаниях среды. В рамках классической теории процесс ВКР можно описать с помощью модели нелинейно связанных осцилляторов.

Собственные частоты колебаний электронов (n₁) и колебаний ядер в молекуле (n₂) определяются по формулам

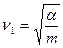, (3.55)

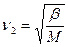, (3.56)

где Х и В – коэффициенты упругости связей в молекуле, m и M – приведенные массы электронного и атомного осцилляторов.

Для реальных молекул частоты колебаний примерно равны n₁ » 10¹⁵ Гц, n₂ » 10¹³ Гц. Если на молекулу воздействует световое поле частоты n₀, то возбуждаются электронные колебания на этой же частоте. Одновременно происходит колебания ядер в молекуле (молекулярные колебания) на частоте n₂. Это могут быть, например, тепловые колебания. Вследствие связи электронных и ядерных движений в молекуле, на электронный осциллятор действует эффективная вынуждающая сила, содержащая колебания на комбинационных частотах n₁-n₂ и n₁+n₂ . Иначе говоря, колебания ядер модулируют электронные колебания в молекуле. В результате молекула переизлучает свет не только на частоте n₀ действующей на нее световой волны, но и на новых – «комбинационных» частотах n₀±n₂. В этом и состоит объяснение явления комбинационного рассеяния света. Колебания на частоте n₀-n₂ . В этом и состоит объяснения явления комбинационного рассеяния света. Колебания на частоте n₀-n₂ возбуждаемые рассеянным излучением называются «стоксовой компонентой». Одновременно создаются колебания на частоте собственных колебаний молекулы n₂­ . В результате комбинационного рассеяния света возникает резонансная сила, возбуждающая молекулярные колебания. Если эта сила достаточно велика, то в системе возникает положительная обратная связь: рассеяние света усиливает молекулярные колебания, а молекулярные колебания усиливают рассеяние света. В результате система самовозбуждается и переходит в режим вынужденного рассеяния, при котором интенсивность рассеяния скачком возрастает на много порядков и становится соизмеримой с интенсивностью лазерного луча.

Пара световых волн (накачка и стоксова компонента) не только резонансно раскачивает колебания, но и фазируют их в большом объеме среды.

Иначе говоря, при ВКР возникает волна когерентных молекулярных колебаний. Эта волна наведена световым полем и эффективно взаимодействует с ним, приводя к усилению излучения на стоксовой частоте. Таким образом, благодаря нелинейности, в ансамбле классических осцилляторов принципиально новые эффекты: фазировка колебаний осцилляторов вследствие их взаимодействие через поле излучения и усиление света. В этом смысле ансамбль нелинейных классических осцилляторов близок к ансамблю квантовых осцилляторов, обеспечивающему когерентность и усиление света в лазере.

Вынужденное рассеяние света можно использовать для преобразования частично когерентного лазерного излучения в энергию полностью когерентного светового пучка на другой (стоксовой) частоте. Эксперименты показывают, что данный метод позволяет значительно (в 100 и более раз) уменьшить угловую расходимость излучения. При этом энергетическая эффективность преобразования составляет обычно 50%.

Потери, связанные с изгибом стекловолокон. Различают микроизгибы (соизмеримые с диаметром сердцевины волокна D) и макроизгибы радиуса R >> D. В первом случае, микроизгиб приводит к образованию механического уплотнения в месте изгиба и, соответственно, к увеличению АПП, что вызывает микрорефракцию. В случае макроизгиба СВ, показанного на рисунке 3.25, область АВ сжимается, область CD растягивается и сердцевина СВ перемещается в направлении стрелки в сторону оболочки СВ.

Световой пучок, распространяющийся по заштрихованной части сердцевины СВ, не имеет обратного пути к центру СВ, после распрямления СВ, и постепенно рассеивается в оболочке.

Потери, связанные с микроизгибами уменьшаются за счет специальных конструкции СВ – кабелей. Потери обусловленные макроизгибами можно свести к минимуму, если радиус закругления задавать достаточно большим, при прокладке кабеля.

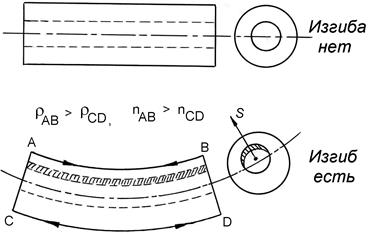
Рисунок 3.25 – Перевод света из сердцевины стекловолокна в оболочку,

при макроизгибе СВ

Термо – механические потери: как уже отмечалось, для защиты СВ от механического разрушения, оно покрывается тонкой пленкой полимера. Поскольку коэффициенты линейного и объемного расширения у СВ и защитной пленки не одинаковы, при температурных колебаниях окружающей среды могут возникнуть локальные (местные) колебания механической плотности ±Dr и, соответственно АПП, ±Dn, что приведет к микрорефракции и рассеянию света. Очевидно, что задача разработчиков СВ сводится к созданию таких защитных покрытий для СВ, у которых температурные коэффициенты расширения и сжатия максимально близки к аналогичным коэффициентам у СВ.

Дифракционные потери в стекловолокнах. Если длина волны l в сердцевине СВ имеет величину порядка 1мкм, а диаметр сердцевины D составляет (5 ¸ 50) мкм, значения l и D можно считать соизмеримыми.

Известно, что в этом случае в процессе распространения света по СВ возникает явление дифракции, то есть расходимости светового пучка и переводу части световой энергии из сердцевины в оболочку. В этом случае условие ПВО перестает выполняться. Одним из эффективных методов борьбы с дифракционными потерями в СВ является создание нелинейной оптической среды. Нелинейная оптическая среда возникает в сердцевине СВ, если в СВ вводится свет повышенной интенсивности. В этом случае, под воздействием света механическая плотность СВ симметрично возрастает от периферии СВ к оси его симметрии и возникает явление самофокусировки, сводящее дифрагирующие лучи к оси симметрии СВ, и восстанавливающее режим ПВО.

Влияние оптического волокна на характеристики сетей связи Тип оптического волокна оказывает существенное влияние на характеристики сетей связи.

Спектральные характеристики различных оптических волокон приведены на рисунке 3.26. Здесь кривая 1 соответствует обычному одномодовому волокну (SMF) позволяющему передавать до 8 каналов в полосах S, C и L.

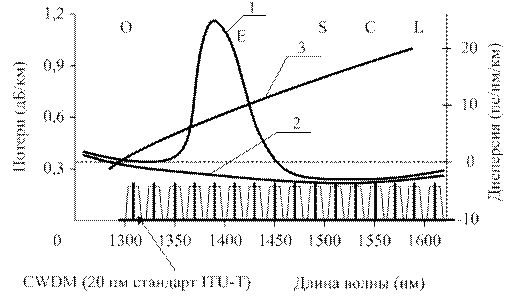
Рисунок 3.26 – Спектральные характеристики и дисперсия различных оптических волокон

Из-за гидроксильного пика фактически исключается область 1,4 мкм из использования для большинства сетевых приложений. Ионы ОН⁺ со временем проникают в обычное волокно SMF. Это не позволяет использовать обычное волокно SMF, даже если начальное затухание в области водяного пика мало, в качестве волокна для систем полного спектрального диапазона.

Волокну с нулевым водяным пиком (ZWPE) соответствует кривая 2.

Волокно ZWPE обладает лучшими характеристиками по затуханию по сравнению с обычным SMF волокном. Однако это волокно имеет относительно высокую дисперсию (-17пс/нм/км при х=1,55 мкм), что иллюстрирует кривая 3 на рисунке. Это ограничивает длину пролета, перекрываемого без регенерации при небольшом числе используемых каналов. Если же требуется большое число каналов, то приходится использовать компенсацию дисперсии. Использование компенсации дисперсии увеличивает потери, что требует увеличения коэффициента усиления усилителей и ведет к росту величины поляризационной модовой дисперсии.

Относительно дешевое магистральное волокно, это волокно с ненулевой смещенной дисперсией NZDSF. Это волокно имеет малую дисперсию и малый наклон дисперсионной характеристики. Уровень дисперсии волокна NZDSF в 3-4 раза меньше, чем у обычного волокна SMF (рисунок 3.27), что позволяет в 3-4 раза увеличить длину некомпенсируемого участка на скоростях 2,5 ÷ 10 Гбит/с. Умеренная величина дисперсии волокна NZDSF обеспечивает не только большую длину полета с существующим оборудованием, но также и экономию средств при реализации сетей.

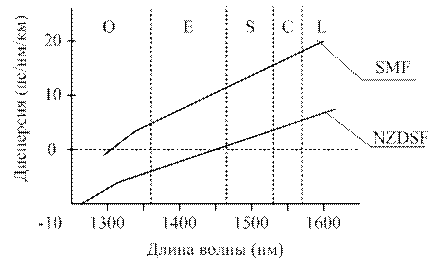
Рисунок 3.27 – Зависимости дисперсии от длины волны оптических волокон

Закон Бугера – Ламберта и оценка полных потерь оптического излучения в стекловолокнах. Из сказанного в разделе 3.16 ясно, что экспериментальное определение конкретного вида потерь в СВ представляет достаточно сложную физико-техническую задачу. С точки зрения эксплуатации СВ-кабеля, нас интересуют полные потери, безотносительно к природе их происхождения.

Известно, что интенсивностью излучения света называется величина, определяемая выражением

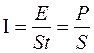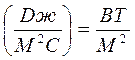, , (3.57)

где Е – энергия оптического излучения, переносимая световой волной через площадь S за время t;

Р – мощность излучения, соответствующая энергии W.

Если интенсивность излучения после входа в СВ равна I₀, то интенсивность света, прошедшего в СВ путь L, уменьшается до величины I < I₀, рисунок 3.28.

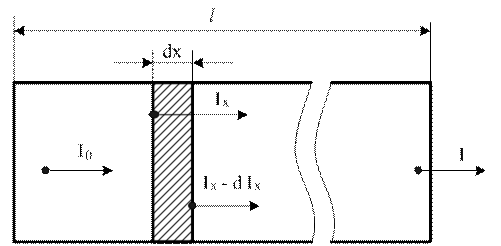
Рисунок 3.28 – К определению потерь в световоде

Выберем внутри СВ малый элемент толщины dx, рисунок 3.26. На входе в этот элемент интенсивность света равна I_Х, а на выходе I_Х – dI_Х, где dI_Х убыль интенсивности. Очевидно, что dI_Х пропорциональна I_Х и dx. Вводя коэффициент пропорциональности b, получаем

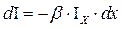(3.58)

Знак «минус» (–) в (3.56) означает убыль интенсивности dI_Х. Разделяя переменные и интегрируя (3.58) имеем , , .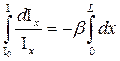

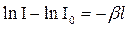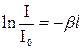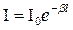. (3.59)

Формула (3.59) носит название закона Бугера – Ламберта. Величина b, входящая в (3.59), называется коэффициентом полных потерь световой энергии в СВ. Уточним физический смысл этой величины. Потребуем выполнения условия

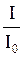= е¹ = е = 2,718282. (3.60)

Из (3.59) и (3.60) следует

е¹ = е^+bl, bl₁ = 1, 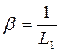, (м^-1). (3.61)

Согласно (3.61), коэффициент полных потерь световой энергии в СВ есть физическая величина, обратная такой длине СВ L₁, на которой интенсивность света убывает в е = 2,718282 раз.

Согласно (3.59) величину b можно представить в виде

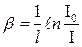(3.62)

Согласно (3.57) и (3.62)

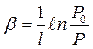(3.63)

Заменяя натуральный логарифм на десятичный имеем из (3.63)

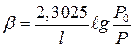(3.64)

Умножая правую и левую части в (3.64) на 10, получаем

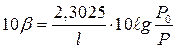(3.65)

Величину

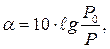(Дб) (3.66)

назовем коэффициентом затухания света в стекловолокне, измеряемом в децибелах. Из (3.65) и (3.66) следует взаимосвязь между b и a в виде

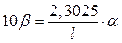, 10b l = 2,3025 a, 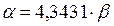l, Дб. (3.67)

Разделим (3.66) на длину L стекловолокна и выразим L в километрах

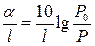, (3.68)

Затухание в является широко распространенной единицей измерений в технике связи.

Методика практического определения коэффициента затухания b. Практическое определение интенсивностей I₀, I входящих в (3.62) согласно рисунка 3.28 не представляется возможным, поскольку датчик интенсивности (или мощности) невозможно внедрить в стекловолокно. На рисунке 3.29 показано соотношение между интенсивностями I₀, I и соответствующими им интенсивностями на входе в СВ (I_ВХ), и на выходе из СВ (I_ВЫХ), а также интенсивностями света, отраженного от левого торца СВ (I_ОТР1) и правого (I_ОТР2).

Рисунок 3.29 – К определению коэффициента затухания

Согласно рисунка 3.29, I₀ = I_ВХ – I_ОТР1 = I_ВХ – I_ВХ ∙ k₁ = I_ВХ (1 – k₁)

I₀ = I_ВХ (1 – k₁) (3.69)

I_ВЫХ = I – I_ОТР2 = I – I ∙ k₂ = I (1 – k₂),

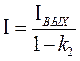(3.70)

где k₁ – коэффициент отражения света от границы раздела «воздух – СВ»;

k₂ – коэффициент отражения света от границы раздела «СВ – воздух».

Разделив почленно (3.69) на (3.70) получим

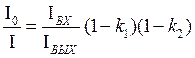(3.71)

Подставляя (3.71) в (3.62), имеем

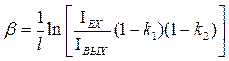(3.72)

Поскольку I_ВХ ~ P_ВХ, I_ВЫХ ~ P_ВЫХ, получаем

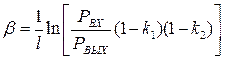(3.73)

Коэффициенты отражения k₁ и k₂ зависят от углов падения и преломления светового пучка, вводимого в СВ через границу «воздух – СВ» и выводимого из СВ через границу «СВ – воздух». Значения коэффициентов k и k 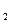определяются формулами Френеля.

При нормальном падении светового пучка на торец СВ,

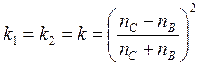, (3.74)

где n_C, n_В – АПП стекла и воздуха – соответственно.

В большинстве случаев, световые пучки вводятся в СВ под углами γ (в соответствии с рисунком 3.11), которые квантуются согласно формуле (3.20). Наклонному падению светового пучка на границу раздела соответствуют коэффициенты отражения k_ТЕ и k_ТМ, зависящие от типа поляризации волны

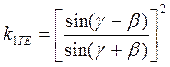(3.75)

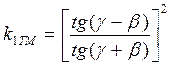(3.76)

Аналогично определяются коэффициенты отражения волны k₂ стекловолокна.