Ширина спектральной линии

До сих пор мы рассматривали ансамбли одинаковых частиц, имеющих, например, энергетические уровни Е₂ и Е₁, между кото­рыми совершаются переходы. При излучательных переходах между уровнями Е₂ и Е₁ различных частиц частота излучения всех частиц по формуле должна быть одинаковой. Однако в соответствии с принципом Паули в системе частиц не может быть больше двух частиц, имеющих одинаковую энергию. Поэтому при образовании ансамбля одина­ковых частиц их энергетические уров­ни несколько расщепляются. Степень размытия уровней определяется соот­ношением Гейзенберга, которое можно записать в форме

DЕDt ³ h, (2.49)

где DЕ и Dt - неопределённости энергии и времени.

Предположим, что необходимо определить частоту излучения при переходе с уровня 2 на основной уровень 1. Вре­мя жизни частиц в возбужденном состоянии определяется: t₂=1/А₂₁. Следует считать, что неопределенность времени равна времени жизни частицы, т.е. Dt=t₂. Подставляя Dt в формулу (2.49), полу­чаем неопределенность энергии уровня 2: DЕ₂ ³ h/t₂. Наиболее широкими оказываются уровни с малым временем жиз­ни. Неопределенность частоты перехода между «размытыми» уровнями 2 и 1 с ширинами DЕ₂ и DЕ₁ находится из со­отношения n_maх–n_min=(DЕ₂ + DЕ₁)/h и определяется суммой неопределенностей энергии обоих уровней. Ширина спектральной линии, определяемая только временем жизни частиц по спонтанному излучению, минимальна и называется есте­ственной шириной спектральной линии. Ширину контура спект­ральной линии принято определять как разность частот, на которых интенсивность I равна половине максимального значения I_о. Частотой перехода (центральной частотой перехода) называют частоту, соответствующую максимуму спектральной ли­нии. Форма спектральной линии может быть представлена так назы­ваемой лоренцевой кривой I/I₀ = Dn² / [(n -n₀)² + Dn²], совпадающей с резо­нансной кривой ко­лебательного конту­ра. Реальные наблю­даемые спектраль­ные линии имеют ширину больше ес­тественной.

Уширение спек­тральной линии из-за столкнове­ний. В газообразных веществах молекулы газа, находясь в тепловом движении, сталкиваются друг с другом; при этом часть таких столкновений носит неупру­гий характер. При неупругих соударени­ях совершается переход между уровня­ми, что сокращает время жизни части­цы на уровне по сравнению с временем жизни, обусловленным спонтанными переходами. Но уменьшение времени жизни на уровне в соответствии с прин­ципом Гейзенберга приводит к увеличению размытости уров­ня DЕ, что в свою очередь приводит к уширению спектра излучения. Для уменьшения эффекта уширения линии излучения при столкно­вениях в некоторых квантовых приборах используются методы, сни­жающие вероятность неупругих столкновений излучающих частиц. Для этого увеличивают длину свободного пробега частиц, заставляя их двигаться в форме остро направленных пучков. Для предотвра­щения сокращения времени жизни при неупругих соударениях со стенками сосуда последние покрывают материалом, при столкнове­ниях с которым частица испытывает только упругое отражение.

Доплеровское уширение спектральной линии. Это уширение связано с эффектом Доплера, т.е. с зависимостью наблюдае­мой частоты излучения от скорости движения излучателя. Если ис­точник, создающий в неподвижном состоянии монохроматическое излучение с частотой n₀, движется со скоростью V в сторону к на­блюдателю так, что проекция скорости на направление наблюде­ния составляет V_х, то наблюдатель регистрирует более высокую частоту излучения

n = n₀ (1 + V_х / с) = n₀ (1 + V cosq / c), (2.50)

где с – фазовая скорость распространения волны; q – угол между на­правлениями движения излучателя и наблюдения.

В квантовых системах источниками излучения являются атомы или молекулы. В газообразной среде при термодинамическом рав­новесии скорости частиц распределены по закону Максвелла – Больцмана. Поэтому и форма спектральной линии всего вещества будет связана с этим распределением. В спектре, регистрируемом наблюдателем, должен быть непрерывный набор частот, так как разные атомы движутся с разными скоростями относительно на­блюдателя. Учитывая лишь проекции скоростей V_x распределении Максвелла – Больцмана, можно получить следующее выражение для формы доплеровской спектральной линии

I = I₀ еxp 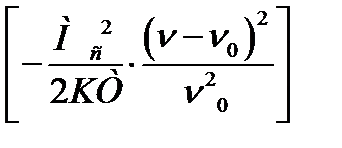. (2.51)

Эта зависимость является гауссовской функцией. Соответствующая значению I₀/2 ширина линии

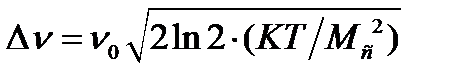. (2.52)

С увеличением массы частиц М и понижением температуры Т шири­на линии Dn уменьшается.

Наблюдаемая спектральная линия вещества представляет со­бой суперпозицию спектральных линий всех частиц вещества, т.е. линий с различными центральными частотами. Для легких частиц при обычной температуре ширина доплеровской линии в оптичес­ком диапазоне может превышать естественную ширину линии на несколько порядков и достигать значения более 1 ГГц.

В квантовых приборах широко используются твердые вещества с примесными ионами, квантовые переходы которых являются ра­бочими. Колебания кристаллической решетки создают переменное электрическое поле, которое влияет на ионы решетки и изменяет их энергию, а это приводит к размытию энергетических уровней и уширению спектральной линии. Кроме того, ширина линии увеличивает­ся вследствие тепловых колебаний самих ионов. Причиной уширения спектральной линии твердого тела может быть также пространс­твенная неоднородность физических параметров среды или неод­нородности электрического и магнитного полей. Причиной уширения спектральной линии может быть также электромагнитное излу­чение, вызывающее вынужденные переходы между рассматривае­мыми уровнями и приводящее к изменению времени жизни частицы. Поэтому, например, процесс генерации излучения в квантовых при­борах будет приводить к изменению ширины линии.