Эксергия неподвижного рабочего тела

Рассмотрим обратимый переход неподвижного рабочего тела из неравновесного состояния в равновесное. Выведем формулу для этой максимально возможной работы. Для того, чтобы рабочее тело находилось в состоянии равновесия с окружающей средой, необходимо изменить его внутреннюю энергию. В соответствии с первым законом термодинамики dU = δQ - δL изменить внутреннюю энергию рабочего тела можно путем подвода или отвода теплоты δQ или за счет совершения работы δL. В случае если процесс обратим, то рабочее тело будет получать или отдавать теплоту при постоянной температуре окружающей среды Т_о. Тогда, в соответствии со вторым законом термодинамики, эта теплота равна

.

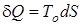Объединяя уравнения первого и второго законов термодинамики, получим

.

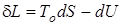По этой формуле определяется работа, которую совершает термодинамическая система при обратимом переходе из равновесного состояния в состояние равновесия с окружающей средой без учета работы, затраченной системой на преодоление сил давления окружающей среды (работа вытеснения окружающей среды), определяемой по формуле р_о·dV,

где р_о- давление окружающей среды; dV – изменение объема рабочего тела.

С учетом работы вытеснения выражение для максимальной работы, совершаемой системой, будет

.

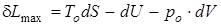Интегрируя последнее уравнение, находим

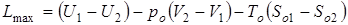, (1.83)

где (U₁ – U₂) – работа обратимого адиабатного процесса приведения рабочего тела в состояние равновесия с окружающей средой;

Т_о(S_о1 – S_о2) – работа, затраченная на приращение энтропии окружающей среды;

S_о1, S_о2 – энтропия окружающей среды соответственно до и после протекания процесса (S_о2 > S_о1).

При обратимом изменении состояния системы (рабочее тело – окружающая среда) суммарное изменение энтропии, очевидно, равно нулю, т.е.

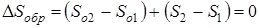, (1.84)

где (S₂ – S₁) – изменение энтропии рабочего тела.

Из последнего выражения следует, что

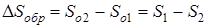. (1.85)

Тогда формула для максимальной работы будет

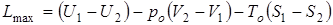. (1.86)

Из этой формулы вытекает, что максимальная работа (эксергия) полностью определяется состоянием рабочего тела в начале и конце процесса и не будет зависеть от пути процесса. Следовательно, эксергия неподвижного рабочего тела является функцией параметров состояния рабочего тела и окружающей среды.

В случае, когда в системе имеют место необратимые изменения состояния, будет справедливо соотношение

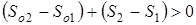, (1.87)

из которого следует 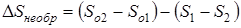, (1.88)

где 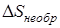- увеличение энтропии системы вследствие необратимости протекающих в ней процессов. При этом полезная работа будет определяться из уравнения

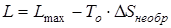, (1.89)

где Т_о·ΔS_необр – потеря работоспособности системы, а уравнение

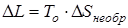(1.90)

называется уравнением Гюи-Стодолы.