Второй закон термодинамики

Прямые и обратные циклы. Термический КПД, коэффициент трансформации теплоты, холодильный коэффициент. Цикл Карно и его циклический КПД. Теорема Карно. Регенеративные цикл. Влияние необратимости на процесс преобразования теплоты в работу.

Второй закон термодинамики. Аналитическое выражение второго закона термодинамики для обратимых и необратимых процессов. Необратимый адиабатный процесс. Эксергия как мера работоспособности. Эксергия теплоты. Потери эксергии в необратимых процессах. Эксергетический КПД. Статистическое истолкование второго закона термодинамики. Энтропия и вероятность. Пределы применимости второго закона термодинамики.

Изменение энтропии идеального газа. Ts – диаграмма газа и ее свойства; hs – диаграмма идеального газа. Таблицы энтропии идеальных газов. Термодинамическая шкала температур. Абсолютный нуль температуры.

По теме не предусмотрены лабораторные и контрольные работы. После изучения теоретического материала следует ответить на вопросы для самопроверки по этой теме. Ответы так же можно найти в учебниках [1,3].

Круговые процессы

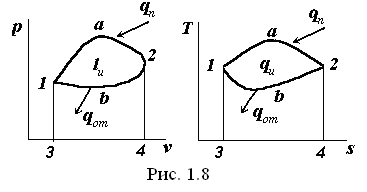
Совокупность процессов, в результате которых термодинамическая система, выведенная из некоторого состояния, возвращается в исходное состояние, называется круговым процессом (циклом). Цикл, протекающий в направлении движения часовой стрелки, называется прямым. По этому циклу работают тепловые машины-двигатели. Цикл – протекающий против хода часовой стрелки, называется обратным. По нему работают холодильные машины, тепловые насосы и др.

Проанализируем течение прямого цикла. На pv-, Ts- диаграммах изображен цикл, состоящий из двух последовательных процессов 1-а-2 и 2-b-1. За счет подвода теплоты q_п к рабочему телу в процессе 1-а-2 термодинамическая система (рабочее тело) расширяется (v₁<v₂), при этом производится работа l_1-a-2, которая численно равна площади фигуры f₁ под линией процесса 1-а-2 (f₁=1-a-2-4-3-1). Далее следует процесс сжатия 2-b-1, который возможен лишь при отводе теплоты q_от от рабочего тела (без отвода теплоты q_от сжатие будет происходить по линии 2-а-1). При сжатии системы внешние силы совершают работу l_2-в-1, численно равную площади фигуры f₂ под линией процесса 2-b-1 (f₂=2-b-1-3-4-2). Очевидно, что разность площадей (f₁-f₂) равна площади замкнутой фигуры (1-a-2-b-1), которая численно равна работе, называемой работой цикла l_ц.

Если учесть, что на Ts-диаграмме площадь под линией процесса численно равна теплоте, участвующей в данном процессе, то аналогичные рассуждения применительно к приведенной выше Ts-диаграмме приводят к выводу, что площадь замкнутой фигуры (1-a-2-b-1) численно равна теплоте цикла q_ц = q_п - q_от.

Из логических рассуждений следует, что теплота цикла q_ц превращается полностью в работу цикла l_ц. Равенство этих величин можно доказать при помощи первого закона термодинамики

.

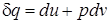Мы рассматриваем круговой процесс, при этом дифференциальное уравнение первого закона термодинамики нужно решать при помощи круговых интегралов

.

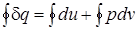Левая часть этого уравнения выражает заключительный результат подвода и отвода теплоты, следовательно, равна (q₁-q₂); первое слагаемое в правой части есть результат изменения внутренней энергии за цикл, он равен 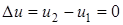, поскольку u₁=u₂ так как внутренняя энергия является функцией состояния; второе слагаемое представляет сумму работ, совершенных за цикл, следовательно, она равна (l_1-a-2 – l_2-в-1). Тогда предыдущее уравнение принимает вид:

.

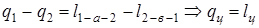В процессе, происходящем по ходу часовой стрелки, теплота превращается в механическую работу, а в процессе против хода часовой стрелки механическая работа превращается в теплоту.

В тепловых двигателях стремятся достичь наиболее полного превращения подведенной теплоты в механическую работу. Для характеристики эффективности циклов тепловых машин вводится понятие термического коэффициента полезного действия h_t (отношение произведенной работы l_п к подведенной теплоте q_п), который показывает какая доля затраченной на цикл теплоты превратилась в механическую работу:

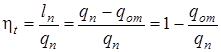. (1.77)

Прямой цикл Карно

Французский физик С.Карно обнаружил, что наиболее благоприятные соотношения получаются в том случае, когда рабочее тело совершает цикл, состоящий из четырех нижеследующих последовательных процессов:

процесс 1-2 изотермическое (при Т₁=const) расширение рабочего тела с подводом теплоты q_п;

процесс 2-3 -адиабатное расширение (q_2-3=0);

процесс 3-4- изотермическое (при Т₂=const) сжатие с отводом теплоты q_от ;

процесс 4-1 - адиабатное сжатие (q_{4 -1}= 0).

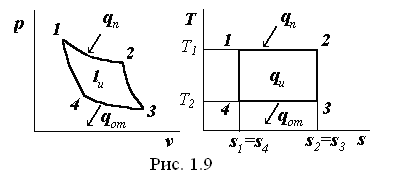
В соответствии с Ts-диаграммой, представленной на (рис. 1.9) подведенная и отведенная теплоты q₁ и q₂ равны площадям под соответствующими линиями процессов

q_п=T₁×(s₂-s₁); q_от=T₂×(s₃-s₄).

Тогда термический КПД цикла Карно определится следующей формулой:

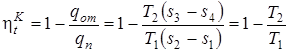, (1.78)

так как (s₃ – s₄)=(s₂ – s₃).

Следует учесть, что из всех циклических процессов цикл Карно обладает наибольшим h_t. Большее значение h_t хотя не противоречит первому закону термодинамики, но невозможно в силу ограничений, накладываемых вторым законом термодинамики.

Теорема Карно: термический КПД цикла Карно не зависит от свойств рабочего тела и определяется только температурами нагревателя и холодильника.

Средствами повышения 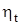являются:

а) повышение температуры источника теплоты T₁;

б) снижение температуры охладителя – Т₂.