Периодичность функции
Функция 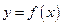 называется периодической функцией, если существует число
называется периодической функцией, если существует число 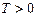 , такое что верно равенство
, такое что верно равенство
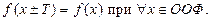
График периодической функции имеет повторяющиеся участки на каждом промежутке длиной T. Наименьшее из чисел T называется наименьшим периодом функции. По умолчанию буквой Т обозначают именно наименьший период, (рис.47).
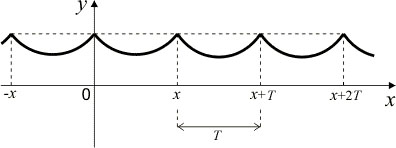
Рис.47
Исследование периодической функции и построение ее графика следует проводить на промежутке, длина которого равна наименьшему периоду функции; этот промежуток часто называют основным промежутком для периодической функции.
Ниже перечислены некоторые свойства периодических функций.
Периодическая функция не может быть задана на множестве, ограниченном сверху или ограниченном снизу.
Например, функция 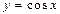 ,
, 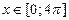 не является периодической.
не является периодической.
Если число 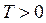 является периодом функции
является периодом функции 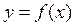 , то число
, то число 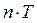 , где
, где 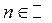 , также является ее периодом.
, также является ее периодом.
Например, функция 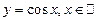 , является периодической, её наименьший период
, является периодической, её наименьший период 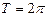 и числа
и числа 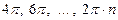 ,
, 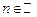 также являются ее периодами.
также являются ее периодами.
Если число 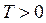 – это наименьший период функции
– это наименьший период функции 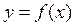 , то функция
, то функция 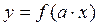 является также периодической и ее наименьший период равен числу
является также периодической и ее наименьший период равен числу 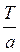 .
.
Например, функция 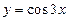 ,
, 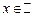 является периодической и ее наименьший период равен
является периодической и ее наименьший период равен 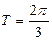 .
.
При сложении двух периодических функций с одинаковыми ООФ получается периодическая функция, причем ее наименьший период делится нацело на 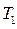 и на
и на 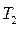 , где
, где 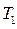 ,
, 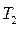 – это наименьшие периоды слагаемых.
– это наименьшие периоды слагаемых.
Например, 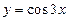 – периодическая с
– периодическая с 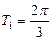 ,
, 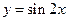 – периодическая с
– периодическая с 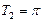
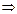
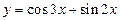 – периодическая с
– периодическая с 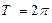 , так как
, так как 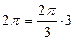 и
и 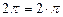 .
.
Примеры (исследование периодичности функций)
1. 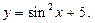 Является ли функция периодической? Чему равен ее наименьший период?
Является ли функция периодической? Чему равен ее наименьший период?
Решение
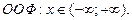 Известно, что основная элементарная функция
Известно, что основная элементарная функция 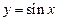 является периодической с наименьшим периодом
является периодической с наименьшим периодом 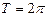 .
.
Проверим равенство 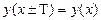 для данной функции:
для данной функции:
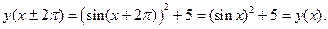
По выполнению равенства заключаем, что данная функция является периодической с периодом 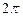 . Чтобы найти наименьший период, понизим степень выражения
. Чтобы найти наименьший период, понизим степень выражения 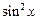 по известной тригонометрической формуле:
по известной тригонометрической формуле: 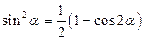 .
.
Тогда 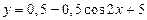
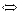
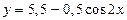 .
.
Теперь имеем сумму двух периодических функций:
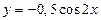 ,
, 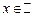
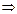
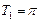 ,
,
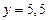 ,
, 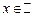
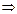 периодом является любое положительное число;
периодом является любое положительное число;
следовательно, данная функция 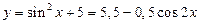 имеет наименьший период
имеет наименьший период 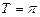 ; поэтому исследовать ее свойства и строить график достаточно на основном промежутке, например при
; поэтому исследовать ее свойства и строить график достаточно на основном промежутке, например при 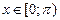 , а затем сделать периодическое продолжение на всю ООФ.
, а затем сделать периодическое продолжение на всю ООФ.
Ответ: функция 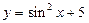 является периодической с наименьшим периодом
является периодической с наименьшим периодом 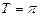 .
.
2. 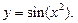 Является ли функция периодической?
Является ли функция периодической?
Решение
Данная сложная функция не является периодической, так как не является периодической её промежуточная функция 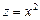 , "искажающая" те значения аргумента x, для которых одинаковые значения имела бы функция
, "искажающая" те значения аргумента x, для которых одинаковые значения имела бы функция 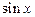 .
.
Для иллюстрации сказанного проверим расположение нулей данной функции:
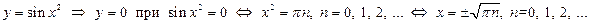 Имеем множество всех нулей функции:
Имеем множество всех нулей функции:
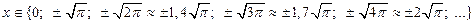

Видим, что нули функции располагаются непериодически на оси OX. Следовательно, данная функция не является периодической (так как в противном случае все её свойства, в том числе и нули, повторялись бы периодически).
Ответ: функция 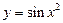 не является периодической.
не является периодической.
3. Укажите, какие из следующих функций являются периодическими?
1) 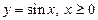 ; 2)
; 2) 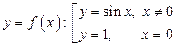 ;
;
3) 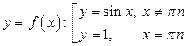 ; 4)
; 4) 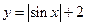 .
.
Решение
1) функция периодической не является, так как равенство 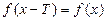 не выполняется, например, для точки
не выполняется, например, для точки 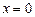 , потому что точка
, потому что точка 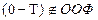 из-за ограниченности снизу ООФ, (рис.48);
из-за ограниченности снизу ООФ, (рис.48);
2) функция периодической не является, так как равенство  не выполняется, например, для точки
не выполняется, например, для точки 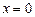 , (рис.49);
, (рис.49);
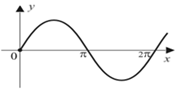
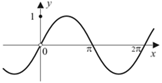
Рис.48 Рис.49
3) функция является периодической с наименьшим периодом 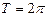 , что хорошо видно по ее графику на рис. 50;
, что хорошо видно по ее графику на рис. 50;
4) функция является периодической с наименьшим периодом 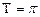 , что хорошо видно по ее графику на рис. 51;
, что хорошо видно по ее графику на рис. 51;
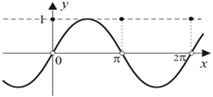
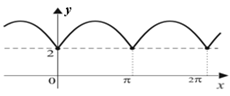
Рис. 50 Рис.51
Ответ: периодическими являются только функции 3) и 4).
Дата добавления: 2021-07-22; просмотров: 678;











