Упражнения для самостоятельной работы
Найдите естественную ООФ следующих функций:
1) 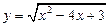 ; 2)
; 2) 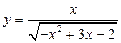 ; 3)
; 3) 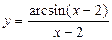 ;
;
4) 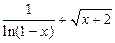 ; 5)
; 5) 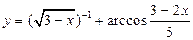 .
.
Найдите множества нулей и промежутков знакопостоянства функций:
1) 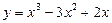 ; 2)
; 2) 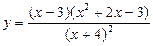 .
.
Охарактеризуйте четность указанных ниже функций:
1) 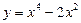 ; 2)
; 2) 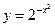 ; 3)
; 3) 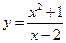 ;
;
4) 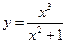 ; 5)
; 5) 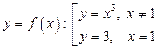 .
.
Какие из следующих функций являются периодическими?
1) 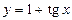 ; 2)
; 2) 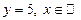 ; 3)
; 3) 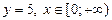 ;
;
4) 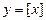 – целая часть
– целая часть 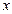 ; 5)
; 5) 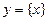 , где
, где 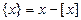 – это дробная часть
– это дробная часть 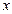 .
.
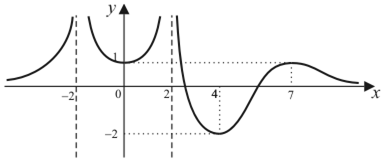
Для функции, заданной графически, запишите:
а) промежутки монотонности;
б) точки локальных экстремумов и соответствующие экстремумы;
в) точные грани функции и ее наименьшее и наибольшее значения.
Ответы к упражнениям для самостоятельной работы
| 1. | 1) 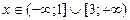 ; ;
| 2) 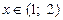 ; 3) ; 3) 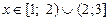 ; ;
| |
4) 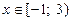 ; ;
| 5) 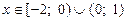 . .
| ||
| 2. | 1) 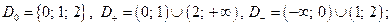
| ||
2) 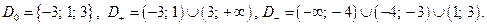
| |||
| 3. | 1) четная; 2) четная; 3) ни четная, ни нечетная; 4) нечетная; 5) ни четная, ни нечетная. | ||
| 4. | 1), 2), 5). | ||
| 5. | а) 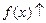 при при 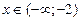 , при , при 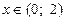 , при , при 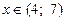 ; ;
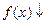 при при 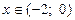 , при , при 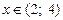 , при , при 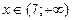 ;
б) точки локальных экстремумов: ;
б) точки локальных экстремумов: 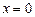 , , 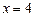 , , 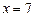 ;
локальные экстремумы: ;
локальные экстремумы: 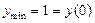 , , 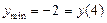 , , 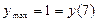 ;
в) ;
в) 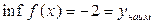 , ,
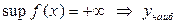 не существует. не существует.
| ||
Вопросы для самопроверки
Что называется глобальными характеристиками функции?
Что такое локальные характеристики функций?
Что называется областью определения числовой функции (ООФ)?
Что называется естественной областью определения функции?
Что называется областью значений числовой функции (ОЗФ)?
Что называется нулем функции?
Что называется промежутком знакопостоянства функции?
Что называется четной функцией?
Что называется нечетной функцией?
Что называется периодической функцией?
Что называется наименьшим периодом функции?
Что называется основным промежутком для периодической функции?
Что такое свойства периодических функций?
Что называется монотонно возрастающей функцией на промежутке?
Что называется монотонно убывающей функцией на промежутке?
Что называется монотонной функцией?
Что называется точкой локального максимума функции?
Что называется максимумом функции?
Что называется точкой локального минимума функции?
Что называется минимумом функции?
Что называется локальными экстремумами функции?
Что называется неубывающей функцией?
Что называется невозрастающей функцией?
Что называется точкой нестрогого локального экстремума?
Что называется наибольшим и наименьшим значениями функции?
Что называется глобальными экстремумами функции на множестве X?
Что называется ограниченной функцией на множестве X?
Глоссарий
глобальными характеристиками функции называется…(стр. 89)
глобальными экстремумами функции на множестве X называется…(стр. 102)
естественной областью определения функции называется…(стр. 90)
локальные характеристики функций это…(стр. 89)
локальными экстремумами функции называется…(стр. 100)
максимумом функции называется…(стр. 100)
минимумом функции называется…(стр. 100)
монотонно возрастающей функцией на промежутке называется…(стр. 99)
монотонно убывающей функцией на промежутке называется…(стр. 99)
монотонной функцией называется…(стр. 99)
наибольшим и наименьшим значениями функции называется…(стр. 102)
наименьшим периодом функции называется…(стр. 96)
невозрастающей функцией называется…(стр. 102)
неубывающей функцией называется…(стр. 102)
нечетной функцией называется…(стр. 94 )
нулем функции называется…(стр. 92)
областью значений числовой функции (ОЗФ) называется…(стр. 90)
областью определения числовой функции (ООФ) называется…(стр. 90)
ограниченной функцией на множестве X называется…(стр. 102)
основным промежутком для периодической функции называется…(стр. 96)
периодической функцией называется…(стр. 95)
промежутком знакопостоянства функции называется…(стр. 92)
свойства периодических функций это…(стр. 96)
точкой локального максимума функции называется…(стр. 99)
точкой локального минимума функции называется…(стр. 100)
точкой нестрогого локального экстремума называется…(стр. 102)
четной функцией называется…(стр. 94)
Дата добавления: 2021-07-22; просмотров: 612;











