Теорема о существовании точных граней ограниченного множества
| Теорема о существовании точных граней ограниченного множества |
| Всякое ограниченное сверху непустое числовое множество имеет точную верхнюю грань, а всякое ограниченное снизу непустое числовое множество имеет точную нижнюю грань. |
w Пусть 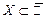 ограничено сверху,
ограничено сверху, 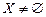 .
.
| Обозначим В — множество чисел, ограничивающих сверху множество Х, (рис. 27). |  Рис. 27
Рис. 27
|
Если 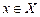 и
и 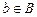 , то из определения числа, ограничивающего множество сверху, следует, что
, то из определения числа, ограничивающего множество сверху, следует, что 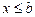 и это верно для
и это верно для 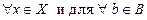 .
.
По свойству непрерывности множества 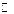 заключаем, что существует число b, такое что выполняется неравенство
заключаем, что существует число b, такое что выполняется неравенство 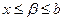 для
для 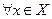 и для
и для 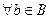 .
.
Но так как 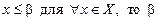 ограничивает Х сверху; так как
ограничивает Х сверху; так как 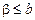 для
для 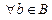 , то b является наименьшим среди всех чисел, ограничивающих множество Х сверху.
, то b является наименьшим среди всех чисел, ограничивающих множество Х сверху.
Поэтому по определению точной верхней грани множества получается, что 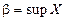 , ч. т. д.
, ч. т. д.
Вторая часть теоремы доказывается аналогичным образом. v
Замечание (к понятию точных граней множества)
1. Для неограниченных сверху множеств часто записывают « 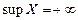 », а для неограниченных снизу – «
», а для неограниченных снизу – «  ».
».
2. Если 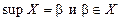 , то обозначается
, то обозначается  , то есть если точная верхняя грань множества принадлежит этому множеству, то она называется максимумом множества.
, то есть если точная верхняя грань множества принадлежит этому множеству, то она называется максимумом множества.
Аналогично, если  , то обозначается
, то обозначается  , то есть если точная нижняя грань множества принадлежит этому множеству, то она называется минимумом множества.
, то есть если точная нижняя грань множества принадлежит этому множеству, то она называется минимумом множества.
Пример 3 (определение максимума и минимума множества)
1) 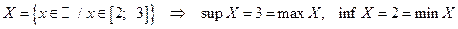 ;
;
2) 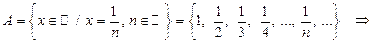
 min A не существует;
min A не существует;
3) 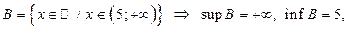 max B и min B не существуют.
max B и min B не существуют.
Дата добавления: 2021-07-22; просмотров: 577;











