Определения ограниченности множества
Рассмотрим некоторое непустое подмножество X множества  .
.
| Определения ограниченности множества ограниченного сверху множества; ограниченного снизу множества; ограниченного множества | |||
|
Множество X, не являющееся ограниченным сверху, называется неограниченным сверху множеством, то есть
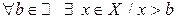 . (1')
. (1')
Множество X, не являющееся ограниченным снизу, называется неограниченным снизу множеством, то есть
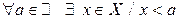 . (2')
. (2')
Множество, не являющееся ограниченным, называют неограниченным множеством, т. е. неограниченное множество является неограниченным сверху или неограниченным снизу или неограниченным и сверху и снизу.
Пример 1 (описания ограниченности множеств)
1) 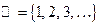 — неограниченное множество, т. к. ограничено снизу (
— неограниченное множество, т. к. ограничено снизу ( 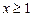 ), но не является ограниченным сверху;
), но не является ограниченным сверху;
2) 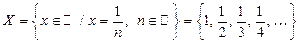 — ограничено, так как ограничено и
— ограничено, так как ограничено и
сверху и снизу: 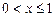 .
.
Замечание (к определениям ограниченности множества)
| 1. | Очевидно из определений (1), (2), (3), что если множество X обладает свойством ограниченности (сверху, снизу или в целом), то можно указать сколько угодно чисел a и (или) b, ограничивающих это множество сверху и (или) снизу. Например, для ограниченного снизу множества 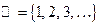 выполняется не только неравенство выполняется не только неравенство 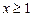 , но и неравенства , но и неравенства 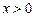 , , 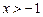 , , 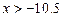 ,… Поэтому все числа a, ограничивающие это множество снизу, образуют множество ,… Поэтому все числа a, ограничивающие это множество снизу, образуют множество 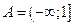 . .
|
| 2. | Сравните определения (1) и (1'), (2) и (2'). Записи (1) и (2) определяют качество ограниченности, записи (1') и (2') определяют отрицание ограниченности, но определяют в позитивной форме, то есть без частицы “не”. Заметьте, что при определении отрицания некоторого понятия символ существования ($) заменяется на символ всеобщности ("), а символ всеобщности заменяется на символ существования. Это есть одно из правил формальной логики, которым пользуются при построении отрицаний в позитивной форме. |
Дата добавления: 2021-07-22; просмотров: 618;

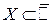 называют ограниченным сверху множеством, если $ число
называют ограниченным сверху множеством, если $ число 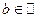 , такое что для
, такое что для 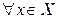 выполняется неравенство
выполняется неравенство 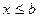 :
:
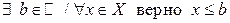 (1)
Число b называется в этом случае числом, ограничивающим сверху множество X.
(1)
Число b называется в этом случае числом, ограничивающим сверху множество X.
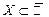 называют ограниченным снизу множеством, если $ число
называют ограниченным снизу множеством, если $ число 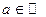 , такое что для
, такое что для 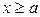 :
:
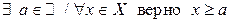 (2)
Число a называется в этом случае числом, ограничивающим снизу множество X.
(2)
Число a называется в этом случае числом, ограничивающим снизу множество X.
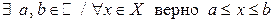 (3)
(3)










