Метод наискорейшего спуска

Метод наискорейшего спуска является итерационным, относится
к методам первого порядка и на каждой итерации требует вычисления
n частных производных минимизируемой функции.

Как и в § 2.2, решаем задачу (2.1.1): найти x^* Î E_n, для которого выполнено условие

f(x^*) = min f(x),

x Î E_n

где x = (x₁, x₂, …, x_n)^т – вектор варьируемых параметров x₁, x₂, …, x_n; n – размерность вектора х; f(x) – вещественная скалярная функция векторного аргумента или функция n-переменных; E_n – n-мерное евклидово пространство.

Метод решения этой задачи представим в виде

x^{(k + 1)} = x^(k) + a_ks^(k), k = 0, 1, 2, …, (2.3.1)

т. е. начиная с некоторой начальной точки x⁽⁰⁾ Î E_n строится последовательность точек x^(k) Î E_n, k = 1, 2, …, которая в общем случае бесконечна и, если метод корректен, должна сходиться к x^* Î E_n – точке минимума функции f(x).

Как известно, вектор градиента Ñf(x) функции f(x)

Ñf(x) = (¶f(x)/¶x₁, ¶f(x)/¶x₂, …, ¶f(x)/¶x_n)^т, (2.3.2)

вычисленный в точке x, задает направление наискорейшего возрастания f(x) при движении из данной точки. Модуль градиента при этом численно равен скорости возрастания. Тогда вектор Ñf(x), обратный по направлению вектору градиента, указывает направление наискорейшего убывания f(x) при движении из точки x. Поэтому естественным является желание выбирать вектор Ñf(x^(k)) в качестве вектора s^(k) на каждом шаге процесса

s^(k) = –Ñf(x^(k)) (2.3.3)

в предложении, что такой выбор будет способствовать максимально быстрому убыванию функции f(x) при переходе от x^(k) к x^{(k + 1)}и в конечном счете приведет к наиболее быстрому определению ее минимума.

Метод наискорейшего спуска можно представить в виде следующего алгоритма:

1. Начать с x⁽⁰⁾ Î E_n, задав e > 0 и k = 0.

2. Вычислить Ñf(x^(k)) = (¶f(x^(k))/¶x₁, ¶f(x^(k))/¶x₂, …, ¶f(x^(k))/¶x_n)^т.

3. Если || Ñf(x^(k)) || £ e, перейти к выполнению п. 7.

4. Найти a_k из решения задачи минимизации функции одной переменной

j(a_k) = min {j(a) = f(x^(k) – a Ñf(x^(k))}. (2.3.4)

a > 0

5. Вычислить x^{(k + 1)} по формуле

x^{(k + 1)} = x^(k) – a_kÑf(x^(k)). (2.3.5)

6. Если || x^{(k + 1)} – x^(k) || / || x^(k) || £ e, перейти к выполнению п. 8.

7. Положить k:=k + 1 и перейти к выполнению п. 2.

8. Процесс окончен: x^(k) – искомая точка минимума функции f(x).

Отметим некоторые важные свойства метода наискорейшего спуска:

1. Является итерационным, относится к методам первого порядка и на каждой итерации требует вычисления n частных производных минимизируемой функции.

2. Для решения одномерной задачи (2.3.4) при выполнении п. 4 алгоритма на каждом шаге может быть использован любой из методов одномерной минимизации. На практике точное решение большого числа одномерных оптимизационных задач не всегда желательно из-за роста вычислительных затрат, поэтому часто ограничиваются достаточно хорошими приближенными решениями, что без видимого ухудшения скорости сходимости метода может существенно уменьшить общий объем вычислительной работы на каждом шаге алгоритма.

3. Демонстрирует хорошие свойства и скорость сходимости на большом удалении от точки локального минимума функции f(x). В непосредственной близости от этой точки существенно ухудшаются практические свойства метода, что вызвано так называемыми "овражными" эффектами. В результате длина шагов значительно уменьшается, вычислительная устойчивость метода падает, поэтому часто не достигается требуемой точности определения решения задачи.

Метод Ньютона

Как и в § 2.3, решается задача (2.1.1): найти x^* Î E_n, для которого выполнено условие

f(x^*) = min f(x),

x Î E_n

где x = (x₁, x₂, …, x_n)^т – вектор варьируемых параметров x₁, x₂, …, x_n;
n – размерность вектора х; f(x) – вещественная скалярная функция векторного аргумента или функция n-переменных; E_n – n-мерное евклидово пространство.

Метод решения этой задачи по-прежнему будем представлять в виде

x^{(k + 1)} = x^(k) + a_ks^(k), k = 0, 1, 2, …

Для определения направления движения из точки x^(k) в точку x^{(k + 1)} осуществим квадратическую аппроксимацию функции f(x) в окрестности точки x^(k):

j(x) = f(x^(k)) + (Ñf(x^(k)), x – x^(k)) + 0.5(x – x^(k))^тH(x^(k))(x – x^(k)). (2.4.1)

Функцию j(x) можно получить, если в разложении функции f(x)
в ряд Тейлора в окрестности точки x^(k) ограничиться первыми тремя членами ряда, отбросив все остальные, имеющие более высокий, чем второй, порядок по (x – x^(k)). Предположим, что вычисленная в точке x^(k) матрица Гессе H(x^(k)) функции f(x) положительно определенная. В этом случае функция j(x) выпуклая и имеет только одну точку минимума, совпада-ющую со стационарной точкой данной функции. Определим эту точку, приравняв градиент функции j(x) к нулевому вектору:

Ñj(x) = Ñf(x^(k)) + H(x^(k))(x – x^(k)) = 0. (2.4.2)

В результате получим систему линейных уравнений относительно (x – x^(k))

H(x^(k))(x – x^(k)) = –Ñf(x^(k)), (2.4.3)

решив которую имеем

(x – x^(k)) = –[H(x^(k))]^-1Ñf(x^(k)). (2.4.4)

Направление

s^(k) = –[H(x^(k))]^–1Ñf(x^(k)) (2.4.5)

будем выбирать для движения из точки x^(k) в точку x^{(k + 1)}. В итоге получим рекуррентную формулу для вычисления x^{(k + 1)} при известном x^(k)

x^{(k + 1)} = x^(k) – [H(x^(k))]^–1Ñf(x^(k)), k = 0, 1, 2, …, (2.4.6)

где [H(x^(k))]^–1 – матрица, вычисленная в точке x^(k)) и обратная матрице Гессе функции f(x).

Рекуррентная формула (2.4.6) "определяет" так называемый метод Ньютона для решения задачи (2.1.1). На практике чаще реализуется другая форма представления метода Ньютона, в соответствии с которой вместо обращения матрицы H(x^(k)) на каждом шаге метода решается система линейных уравнений (2.4.3). В этом случае метод Ньютона записывается в виде

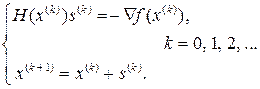(2.4.7)

Решение задачи начинаем с некоторой точки x⁽⁰⁾ Î E_n. Тогда метод Ньютона может быть представлен в виде процедуры, аналогичной процедуре метода наискорейшего спуска с той лишь разницей, что направление s^(k) находится на каждом шаге решения системы линейных уравнений, а длина шага не нуждается в определении.

Пусть функция f(x) дважды непрерывно дифференцируемая. В этом случае метод Ньютона для решения задачи (2.1.1) можно записать в виде следующего алгоритма:

1. Начать с x⁽⁰⁾ Î E_n, задав e > 0 и k = 0.

2. Вычислить Ñf(x^(k)) = (¶f(x^(k))/¶x₁, ¶f(x^(k))/¶x₂, …, ¶f(x^(k))/¶x_n)^т.

3. Если || Ñf(x^(k)) || £ e, перейти к выполнению п. 9.

4. Вычислить H_k = H(x^(k)) и составить систему линейных уравнений:

H_ks^(k) = –Ñf(x^(k)). (2.4.8)

5. Найти s^(k) из решения системы (2.4.8).

6. Вычислить x^{(k + 1)} по формуле

(x^{(k + 1)} = x^(k) + s^(k)).

7. Если || x^{(k + 1)} – x^(k) || / || x^(k) || £ e, перейти к выполнению п. 9.

8. Положить k:= k + 1и перейти к выполнению п. 2.

9. Процесс окончен: x^(k) – искомая точка минимума f(x).

Отметим характерные особенности метода Ньютона:

1. Является итерационным, относится к методам второго порядка и на каждой итерации требует вычисления n частных производных первого порядка и n² частных производных второго порядка минимизируемой функции.

2. При выполнении условий сходимости сходится к решению задачи с квадратической скоростью.

3. Помимо вычисления частных производных на каждом шаге необходимо решать систему линейных уравнений n-го порядка или обращать матрицу этой системы. В результате объем вычислительных операций
на каждом шаге метода Ньютона достаточно велик.

4. Не обладает свойством глобальной сходимости в том смысле, что неудачный выбор начального приближения x⁽⁰⁾ может привести к расходимости метода. Начальное приближение x⁽⁰⁾ рекомендуется выбирать в достаточной близости к локальному экстремуму минимизируемой функции.

5. Для квадратической функции f(x) находит решение задачи (2.1.1) за один шаг.

Существует много модификаций метода Ньютона, которые используются для снижения объема вычислительных операций на каждом шаге или обеспечения сходимости метода при любом начальном приближении x⁽⁰⁾. Так, например, матрица H_k вычисляется либо один раз (H₀) и затем используется без изменения на всех итерациях, либо вычисляется заново через фиксированное (более чем один раз) количество итераций H₀, H_s, H_2s, … (s > 1), а для промежуточных итераций в качестве H_k^-1 используется последняя из вычисленных матриц. Такие модификации метода Ньютона имеют целью уменьшить количество вычисляемых матриц H_k, одновременно снижая трудоемкость многократного решения системы линейных уравнений (2.4.8). При выполнении некоторых дополнительных условий эти модификации часто сохраняют достаточно высокую скорость сходимости.

К другой группе относятся модификации метода Ньютона с регулировкой шага. В этом случае очередное приближение x^{(k + 1)} определяется по формуле

x^{(k + 1)} = x^(k) + a_k s^(k), k = 0, 1, 2, …,

где числовой параметр 0 < a_k £ 1 задает длину шага из x^(k) в направле-
нии s^(k); при этом значение параметра a_k часто определяется из решения одномерной задачи

j(a_k) = min {j(a) = f(x^(k) + a s^(k)}.

a > 0

Главной целью такого подхода является стремление уменьшить зависимость сходимости метода от выбора начального приближения x⁽⁰⁾. Метод Ньютона часто используется в комбинации с другими методами, например с методом наискорейшего спуска, который достаточно быстро находит хорошее приближение к решению задачи, используемое в качестве начального для метода Ньютона. Подробное описание таких подходов имеется во многих руководствах по вычислительной математике.