В форме кинетической энергии

Рассмотрим состояние механизма при двух различных положениях ведущего звена, разделяемых каким-либо промежутком времени dt или углом dφ поворота ведущего звена – кривошипа (рис. 4.4).

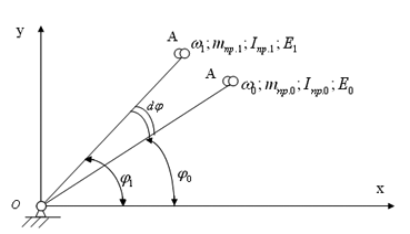
Рис. 4.4. Кинематические и динамические параметры

механизма при различных положениях звена приведения

При положении кривошипа φ₀ угловая скорость звена приведения – ω₀, I_пр.0 – приведенный момент инерции механизма в рассматриваемом положении.

При положении φ₁= φ₀+dφ угловая скорость звена приведения – ω₁, I_пр.1 – приведенный момент инерции механизма.

Изменение кинетической энергии механизма ΔЕ за этот промежуток времени будет равно разности работ сил движущих А_дв и сил сопротивления А_сопр, выполненных за это время (или избыточной работе ):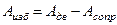

ΔЕ = А_дв- А_сопр= А_изб. (4.4)

ΔЕ = Е₁ - Е₀ = 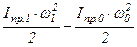, (4.5)

где Е₀ и Е₁ – величины кинетических энергий механизма при положениях φ₀ и φ₁ кривошипа.

А_дв = 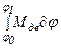, (4.6)

А_сопр = 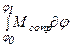, (4.7)

где М_дв и М_сопр – приведенные моменты сил движущих и сил сопротивлений.

Подставив (4.5-4.7) в (4.4), получим:

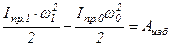(4.8)

Из (4.8) выразим угловую скорость кривошипа при положении :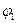

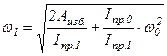(4.9)

Уравнение (4.9) называют уравнением движения машины в форме кинетической энергии.