Схемы с выбором главного элемента

1. Схема с выбором главного элемента без перестановки столбцов.

На каждом из n -1 шагов прямого хода метода выбирают главный элемент как максимальный по модулю среди элементов соответствующего столбца преобразованной матрицы, расположенных на главной диагонали матрицы и ниже: 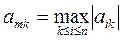, затем осуществляется перестановка уравнений системы (строк расширенной матрицы) так, чтобы строка с номером 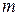заняла k-е место, стала ведущей. После перестановки осуществляются расчеты по формулам (2)-(3) и переход к следующему шагу.

2. Схема с выбором главного элемента с перестановкой столбцов.

Выбор главного элемента 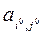на k-ом шаге прямого хода осуществляется среди всех элементов расширенной матрицы, за исключением элементов строк с номерами 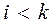и элементов ( 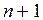) - го столбца. После этого осуществляется перестановка строк и столбцов расширенной матрицы таким образом, чтобы элемент 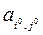стал ведущим, т.е переместился наместо 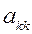. При этом необходимо хранить в памяти ЭВМ строку перестановок столбцов, чтобы восстановить порядок переменных 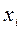при обратном ходе.

Схемы Гаусса просто реализуются и выгодны для систем с плотно заполненной матрицей (когда мало нулевых элементов). Число арифметических операций во всех схемах порядка n³. Если система плохо обусловлена, то точность не гарантируется.

Задачи

1. Решить систему методом Гаусса. Исходные данные считать верными в написанных знаках.

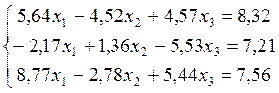
Решение. Прямой ход. Используем схему единственного деления. Все расчеты выполняем с запасным десятичным знаком, результаты заносим в таблицу.

№ шага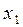
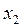
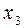
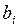
k=0	5,64	-4,52	4,57	8,32	Ведущая строка –
	-2,17	1,36	-5,53	7,21	первая,
	8,77	-2,78	5,44	7,56	ведущий элемент .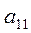
k=1		-0,801	0,810	1,475	Ведущая строка –
		-0,379	-3,772	10,411	вторая,
		4,248	-1,666	-5,377	ведущий элемент .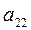
k=2		-0,801	0,810	1,475
			9,950	-27,464
			-43,937	111,303	Прямой ход закончен.

Обратный ход: ; ; .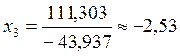

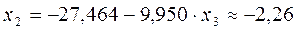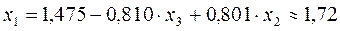Невязки: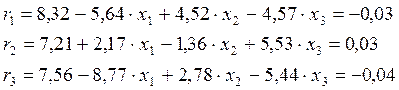

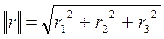= 0,06.

Ответ: x₁ = 1,72; x₂ = -2,26; x₃ = -2,53.

2. Решить систему методом Гаусса с выбором главного элемента с перестановкой столбцов. Исходные данные считать верными в написанных знаках.

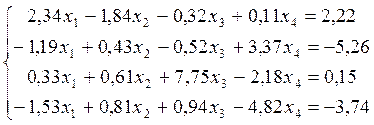
Решение. Прямой ход. Заносим все вычисления в таблицу.

№ шага	Порядок столбцов
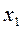
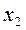
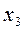
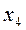
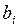
k=0	2,34	-1,84	-0,32	0,11	2,22	Главный элемент: .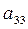
	-1,19	0,43	-0,52	3,37	-5,26	Меняем местами
	0,33	0,61	7,75	-2,18	0,15	1-ю и 3-ю строки,
	-1,53	0,81	0,94	-4,82	-3,74	1-й и 3-й столбцы.
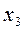
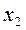
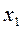
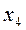
	7,75	0,61	0,33	-2,18	0,15	Ведущая строка: 1-я.
	-0,52	0,43	-1,19	3,37	-5,26
	-0,32	-1,84	2,34	0,11	2,22
	0,94	0,81	-1,53	-4,82	-3,74
k=1		0,079	0,043	-0,281	0,019	Главный элемент: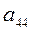
		0,470	-1,168	3,224	-5,250	Меняем местами
		-1,815	2,354	0,020	2,226	2-ю и 4-ю строки,
		0,736	-1,570	-4,556	-3,758	2-й и 4-ый столбцы.
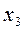
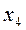
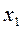
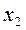
		-0,281	0,043	0,079	0,019	Ведущая строка: 2-я.
		-4,556	-1,570	0,736	-3,758
		0,020	2,354	-1,815	2,226
		3,224	-1,168	0,470	-5,250
k=2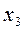
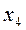
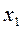
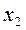
		-0,281	0,043	0,079	0,019	Главный элемент: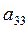
			0,345	-1,162	0,825	на нужном месте,
			2,347	-1,812	2,210	перестановки не делаем.
			-2,279	0,992	-7,909	Ведущая строка: 3-я.
k=3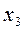
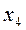
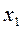
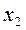
		-0,281	0,043	0,079	0,019
			0,345	-1,162	0,825
				-0,772	0,942
				-0,767	-5,764	Прямой ход закончен.

Обратный ход: ;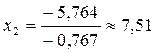

;

;

.

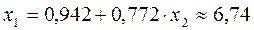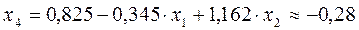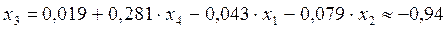Невязки: ;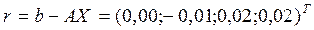

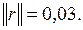
Ответ: x₁ = 6,74; x₂ = 7,51; x₃ = -0,94; x₄ = -0,28.

Метод Жордана

Этот метод, как и метод Гаусса, является методом исключения, предназначенным для системы линейных уравнений 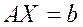( матрица А – невырожденная). Отличие от схем метода Гаусса в том, что путем преобразований матрица А приводится не к треугольному, а к диагональному виду. В результате исходная система линейных уравнений приобретает вид:

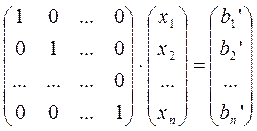
Обратный ход в схемах Жордана становится формальностью.