Задачи для самостоятельного решения

1. Найти нормы векторов i = (1, 0, 0)^T , z = (1, 2, 3, -4)^T.

Ответы: .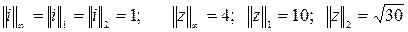

2. Найти нормы матрицы .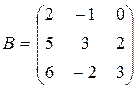

Ответы: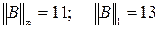

Литература:

[4], т.II, гл. 6, §7.

[5], гл. II, §2.5, упражнение №7 к §2.

§4 Прямые методы решения систем линейных алгебраических уравнений с квадратной матрицей

Постановка задачи. Дана система линейных уравнений 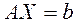, где

; .

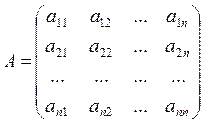Требуется найти решение системы – вектор 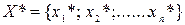. Если матрица системы А – невырожденная, то система имеет единственное решение.

Все методы решения поставленной задачи можно разбить на две группы – прямые итерационные методы.

Прямые методы решения позволяют найти Х* за конечное число шагов. Если исходные данные – точные, то, производя вычисления без округлений (в простых дробях), мы получаем точное решение системы. Однако, при больших 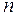это невозможно. При решении все промежуточные вычисления осуществляют с одним-двумя запасными знаками, а результат округляют до требуемой точности, либо оставляют столько знаков после запятой, сколько их в исходных данных (коэффициентах системы).

Погрешность полученного решения 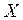характеризует норма вектора невязки 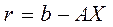, т.е. число .

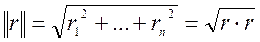Метод Гаусса

Дана система уравнений 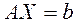(1). Будем считать, что матрица системы А – неособенная. Требуется найти решение системы – вектор Х*.

Метод Гаусса - это метод исключения. На k-ом шаге осуществляется исключение неизвестной 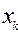из уравнений с номерами i > k, k = 1,…n -1. В результате, за n -1 шаг матрица А приводится к верхнему треугольному виду (прямой ход). Система приобретает вид:

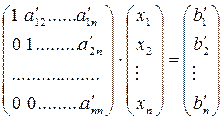
После этого легко найти неизвестные 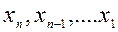(обратный ход). Различные реализации метода Гаусса отличаются способом выбора ведущего элемента.