Задачи для самостоятельного решения
1. Произвести изоляцию корней для уравнений:
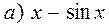 = 0,25;
= 0,25; 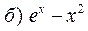 = 0;
= 0; 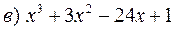 = 0.
= 0.
Ответы: 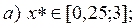
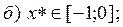
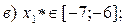
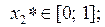
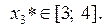
2. Решить уравнения из 1-ой задачи, используя разные методы, с точностью 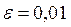 .
.
Ответы:
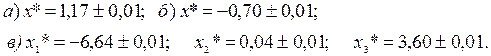
Литература:
[1], гл. IV, работы №2 - 5.
[2], часть 2, гл IX, §1, №1164 – 1167,1169-1177.
[3], гл. X, §3, №3141 – 3155, 3158, 3159.
[5], гл. III, §3.3 – 3.8, упражнения №1 – 4 к главе III.
§3 Нормы вектора и матрицы
Нормой вектора называют некоторую числовую функцию компонент вектора, удовлетворяющую определенным свойствам. Аналогично может быть определена норма матрицы А. При этом норму матрицы вводят так, чтобы она была определенным образом связана (согласована) с используемой нормой вектора. Такие матричные нормы называют согласованными. Наименьшая из согласованных матричных норм носит название подчиненной или операторной нормы.
Для вектора 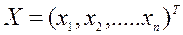 , могут быть, в частности, введены следующие нормы:
, могут быть, в частности, введены следующие нормы:
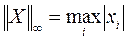 ;
;
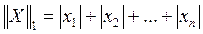 ;
;
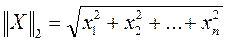 - евклидова норма.
- евклидова норма.
Соответствующие подчиненные нормы матрицы А вводятся следующим образом:
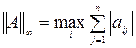 ; (1)
; (1)
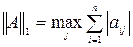 ; (2)
; (2)
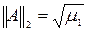 . (3)
. (3)
где i – номер строки, j – номер столбца матрицы A, 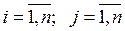 , m1 - максимальное по модулю собственное число матрицы АТА. Первые две матричные нормы легко вычисляются. Что касается последней, то она часто бывает удобной для анализа, но непосредственное вычисление ее в общем случае затруднительно. Поэтому в приведенных ниже примерах и задачах
, m1 - максимальное по модулю собственное число матрицы АТА. Первые две матричные нормы легко вычисляются. Что касается последней, то она часто бывает удобной для анализа, но непосредственное вычисление ее в общем случае затруднительно. Поэтому в приведенных ниже примерах и задачах 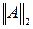 как правило не вычисляется.
как правило не вычисляется.
Задачи
1. Вычислить нормы векторов: X = (2, -2, 1)T и Y = (2, 0, -3, 1)T.
Решение. 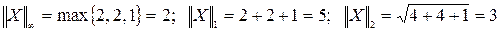 .
.
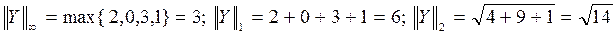 2. Найти нормы матриц:
2. Найти нормы матриц:
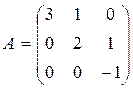 и
и 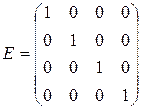 .
.
Решения.
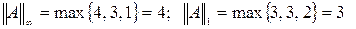 ;
; 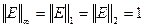 ;
;
Дата добавления: 2021-07-22; просмотров: 458;











