Метод хорд и касательных
Преимущество этого метода в том, что при тех же предположениях относительно 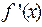 и
и 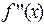 , что и в методе Ньютона, мы получаем последовательные приближения
, что и в методе Ньютона, мы получаем последовательные приближения  и
и 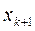 , лежащие по разные стороны от
, лежащие по разные стороны от  , поэтому можно следить за достигнутой точностью в процессе решения. Пусть
, поэтому можно следить за достигнутой точностью в процессе решения. Пусть 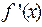 и
и 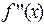 не меняют знак на
не меняют знак на  .
.
Если 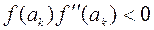 , то расчеты ведут по формулам:
, то расчеты ведут по формулам:

 (9)
(9)
Если 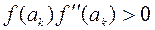 , то
, то
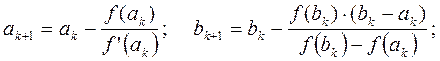
 (10)
(10)
За начальный промежуток 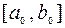 принимают
принимают 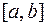 . В результате расчетов получаем последовательность вложенных промежутков
. В результате расчетов получаем последовательность вложенных промежутков  , таких, что
, таких, что  . В качестве критерия остановки расчетов может быть использовано выполнение неравенства:
. В качестве критерия остановки расчетов может быть использовано выполнение неравенства:  . Тогда приближенное решение считают равным
. Тогда приближенное решение считают равным 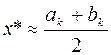 .
.
Задачи
1. Уточнить корень уравнения 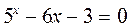 (
(  ) методом деления отрезка пополам. Точность
) методом деления отрезка пополам. Точность 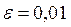 .
.
Решение. Так как процесс вычисления этим методом сходится медленно, уменьшим промежуток изоляции. Возьмем [-0,5; -0,2] 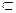 [-1; 0]. Проверка:
[-1; 0]. Проверка: 
 , следовательно,
, следовательно, 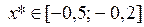 . Теперь уточняем корень.
. Теперь уточняем корень.
Номер шага 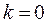 .
.  .
.
Затем 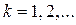 .находим
.находим  . Вычисления производим с запасным десятичным знаком. Результаты расчетов заносим в таблицу. (Стрелки указывают перенос значений
. Вычисления производим с запасным десятичным знаком. Результаты расчетов заносим в таблицу. (Стрелки указывают перенос значений  при
при  и
и  ).
).

| 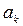
|  
| 
| 
|
 0 0
| -0,5 | -0,2 | -0,35 | -0,331 <0 |
 1 1
| -0,5 | -0,35 | -0,425 | 0,055 >0 |
 2 2
| -0,425 | -0,35 | -0,3875 | -0,139 <0 |
| -0,425 | -0,3875 | -0,406 | -0,044 <0 | |
| -0,425 | -0,406 | -0,416 | 0,008 >0 | |
| -0,416 | -0,406 | -0,411 |
Процесс закончен, т.к.  :
: 
Ответ:  .
.
2. Составить расчетные формулы для определения методом простых итераций корней уравнения  . Найти один из корней с точностью
. Найти один из корней с точностью  . Корни уравнения лежат в промежутках:
. Корни уравнения лежат в промежутках: 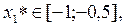

 (см. п. 2.1).
(см. п. 2.1).
Решение. Для уточнения  и
и  можно использовать функцию
можно использовать функцию  , полученную из уравнения. Здесь
, полученную из уравнения. Здесь  ;
;  . Условие сходимости
. Условие сходимости  выполнено и на промежутке [-1; -0,5], и на [1; 1,5], т.к.
выполнено и на промежутке [-1; -0,5], и на [1; 1,5], т.к.  , если
, если 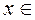 [-1; -0,5] и
[-1; -0,5] и  , если
, если  [1; 1,5]. Значит, для уточнения этих корней можно использовать расчетную формулу
[1; 1,5]. Значит, для уточнения этих корней можно использовать расчетную формулу  ,
,  .
.
Для уточнения  эта формула не годится, т.к.
эта формула не годится, т.к.  терпит бесконечный разрыв в точке
терпит бесконечный разрыв в точке 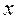 = -0,2
= -0,2  . Можно из исходного уравнения выразить
. Можно из исходного уравнения выразить 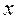 по-другому:
по-другому:  . Здесь
. Здесь 
 . Условие
. Условие  выполнено при
выполнено при  [-0,5; 0].
[-0,5; 0].
Уточним корень  , используя формулу
, используя формулу  . В качестве
. В качестве  можно взять любую точку промежутка изоляции, например,
можно взять любую точку промежутка изоляции, например,  . Дальнейшие расчеты приведены в таблице.
. Дальнейшие расчеты приведены в таблице.
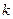
| 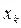
|
| -0,25 | |
| -0,20098 | |
| -0,20033 |
Расчеты закончены, т.к.  0,001. Ответ:
0,001. Ответ:  .
.
3. Найти один из корней уравнения  методом касательных и методом хорд с точностью
методом касательных и методом хорд с точностью  0,01.
0,01.
Решение. Изоляция корня. Уравнение имеет 2 корня, причем  . Проверка (для второго корня):
. Проверка (для второго корня):  .
.
Уточнение корня. а) Метод касательных.
Функция  непрерывная, дважды дифференцируемая,
непрерывная, дважды дифференцируемая,  . В качестве
. В качестве  нужно взять тот конец промежутка [1; 2], где
нужно взять тот конец промежутка [1; 2], где  . Т.к.
. Т.к.  , то
, то  . Результаты расчетов приведены в таблице.
. Результаты расчетов приведены в таблице.
| k |
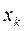
|

|
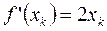
| 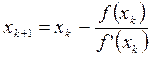
|
| 1,5 | ||||
| 1,5 | 0,25 | 1,417 | ||
| 1,417 | 0,008 |
Вычисления прекращаем, т.к.  . Ответ:
. Ответ:  .
.
б) Метод хорд  . Производные сохраняют знак на промежутке [1;2], т.к.
. Производные сохраняют знак на промежутке [1;2], т.к. 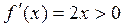 и
и  . Поскольку выполнено условие
. Поскольку выполнено условие  , считаем, что
, считаем, что  . Далее вычисляем по формуле:
. Далее вычисляем по формуле:

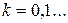 .
.
Результаты расчетов заносим в таблицу.
| k | 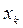
| 
|
| -1 | ||
| 1,333 | -0,222 | |
| 1,400 | -0,04 | |
| 1,412 | -0,007 |
Вычисления прекращаем, т.к.  . Ответ:
. Ответ:  .
.
Дата добавления: 2021-07-22; просмотров: 508;











