Метод Ньютона – Рафсона (метод касательных)

Пусть по-прежнему 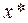- корень уравнения

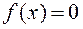(1)

и 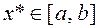. Будем считать, что на 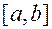функция имеет производные и 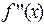, причем , а 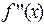сохраняет знак на 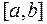. Если начальное приближение 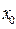взять так, чтобы было выполнено условие

(5)

то последовательность , где

(6)

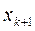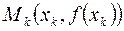будет монотонно сходиться к решению уравнения - точке . Геометрический смысл формулы (6) заключается в том, что на каждом шаге определяется - точка пересечения касательной к графику функции , проведенной в точке , с осью OX. На следующем шаге касательную строим в точке и т.д.

Метод Ньютона сходится быстрее метода хорд, для него справедливо при указанных выше свойствах функции f(x) соотношение

² ,

что соответствует так называемой квадратичной скорости сходимости. Этот метод не обладает свойством глобальной сходимости, при выборе нужно следить за выполнением условия (5). К недостаткам метода Ньютона - Рафсона следует отнести также необходимость вычисления на каждом шаге метода не только значения функции, но и ее производной, что на практике может существенно увеличить объем вычислений, требуемых для выполнения каждой итерации метода.