Метод простой итерации
Уравнение
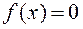 (1)
(1)
тем или иным образом разрешают относительно х и приводят к виду
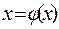 . (2)
. (2)
Затем, начиная с некоторого 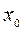 , по рекуррентной формуле:
, по рекуррентной формуле:
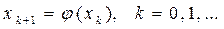 .
.
строится последовательность 
 .
.
В качестве начального приближения можно взять любую точку 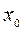 из промежутка изоляции
из промежутка изоляции 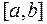 . Для сходимости метода достаточно обеспечить выполнение условия:
. Для сходимости метода достаточно обеспечить выполнение условия:
 , (3)
, (3)
(чем ближе  к нулю, тем быстрее фактическая сходимость).
к нулю, тем быстрее фактическая сходимость).
В качестве критерия остановки расчетов может быть использовано выполнение соотношения: 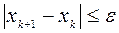 . Приближенное значение корня – последнее вычисленное значение x, т.е.
. Приближенное значение корня – последнее вычисленное значение x, т.е. 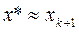 .
.
Метод простой итерации прост в реализации, сходится при выполнении достаточных условий сходимости, например, (3).
Метод хорд
Если известно, что корень уравнения
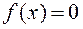 (1)
(1)
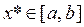 , а функция
, а функция  непрерывна на
непрерывна на 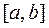 и имеет производные
и имеет производные 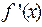 и
и 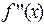 , которые сохраняют знак на
, которые сохраняют знак на 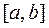 , то для уточнения
, то для уточнения 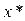 можно использовать метод хорд в приведенной ниже редакции.
можно использовать метод хорд в приведенной ниже редакции.
В качестве  берут тот конец промежутка
берут тот конец промежутка 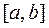 , где
, где 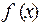 и
и 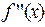 имеют противоположные знаки. Итерационный процесс построения последовательности
имеют противоположные знаки. Итерационный процесс построения последовательности  , сходящейся к
, сходящейся к 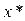 описывается формулами:
описывается формулами:
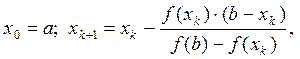 если
если 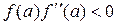 , (4)
, (4)
и 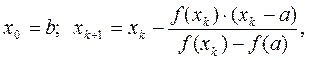 если
если 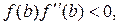 (4а)
(4а)
где 

|
В первом случае на каждом шаге находят точку пересечения 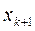 хорды графика
хорды графика 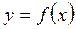 , проходящей через точки
, проходящей через точки 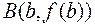
 и
и 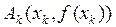 с осью ОX (см. рисунок). На следующем шаге строят хорду, проходящую через точки
с осью ОX (см. рисунок). На следующем шаге строят хорду, проходящую через точки 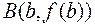 и
и 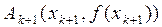 и т.д. Все значения
и т.д. Все значения 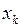 дают приближение корня
дают приближение корня 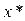 с недостатком. Во втором случае неподвижной точкой является
с недостатком. Во втором случае неподвижной точкой является 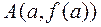 , и значения
, и значения 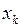 дают приближение корня
дают приближение корня 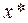 с избытком.
с избытком.
В знаменателях формул (4) и (4а) стоит разность значений функции, которая вблизи корня становится малой, что ведет к потере значащих цифр. Это ограничивает точность расчетов, особенно для случая кратного корня 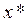 . Поэтому метод хорд используют до тех пор, пока
. Поэтому метод хорд используют до тех пор, пока  убывает. Далее для уточнения корня можно использовать другой способ, например, метод деления отрезка пополам.
убывает. Далее для уточнения корня можно использовать другой способ, например, метод деления отрезка пополам.
Критерий остановки расчетов: 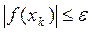 . Приближенным значением корня функции f(x) считают последнее вычисленное значение:
. Приближенным значением корня функции f(x) считают последнее вычисленное значение:  .
.
В общем случае метод хорд можно записать с помощью следующего соотношения:
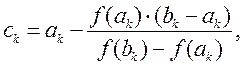 k = 0,1,2,.. (4b)
k = 0,1,2,.. (4b)
За начальный промежуток 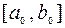 принимают
принимают 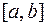 . После вычисления по формуле (4b) новый промежуток
. После вычисления по формуле (4b) новый промежуток 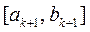 формируется на основании сравнения знака функции в точке
формируется на основании сравнения знака функции в точке 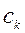 и в точках
и в точках 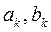 .
.
Дата добавления: 2021-07-22; просмотров: 484;











