Задачи для самостоятельного решения
Действия с приближенными величинами
Основные понятия
Пусть 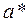 – точное значение некоторой величины, а число
– точное значение некоторой величины, а число 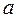 - приближенное значение этой величины (для простоты будем называть
- приближенное значение этой величины (для простоты будем называть 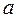 приближенным числом). Величину
приближенным числом). Величину 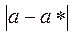 называют абсолютной погрешностью числа
называют абсолютной погрешностью числа 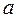 . Предельной абсолютной погрешностью
. Предельной абсолютной погрешностью 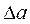 числа
числа 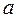 называют наименьшую из верхних границ величин
называют наименьшую из верхних границ величин 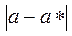 , т.е.
, т.е.
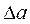 =
= 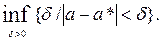 Это означает, что если
Это означает, что если 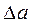 - предельная абсолютная погрешность числа
- предельная абсолютная погрешность числа 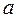 , то
, то 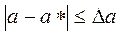 , т.е.
, т.е. 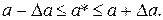 Обычно записывают так:
Обычно записывают так: 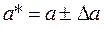 , например,
, например, 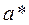 = 8,341
= 8,341 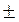 0,005.
0,005.
В дальнейшем будем называть предельную абсолютную погрешность просто абсолютной погрешностью.
Предельной относительной погрешностью числа 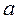 называют величину
называют величину 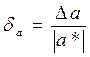 или
или 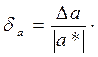 100%. В случае, когда
100%. В случае, когда 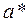 неизвестно, полагают, что
неизвестно, полагают, что 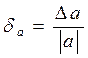 или
или 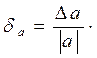 100%.
100%.
В дальнейшем будем называть предельную относительную погрешность числа просто относительной погрешностью.
Пусть 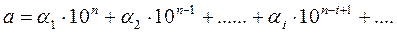 ,
,
где a1 , a2 , ..., ai ...- целые числа, принимающие значения от 0 до 9.
Значащими цифрами числа 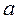 называют все его цифры, начиная с первой слева ненулевой цифры.
называют все его цифры, начиная с первой слева ненулевой цифры.
Обычно при записи значений погрешностей в соответствующих числах оставляют одну-две значащих цифры, например: 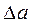 = 0,03,
= 0,03, 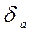 = 5%.
= 5%.
Количество верных знаков числа 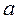 отсчитывают от его первой значащей цифры до цифры
отсчитывают от его первой значащей цифры до цифры 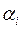 , для которой еще выполнено одно из неравенств:
, для которой еще выполнено одно из неравенств:
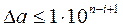 , если
, если 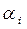 - верная в широком смысле;
- верная в широком смысле;
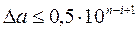 , если
, если 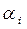 - верная в узком смысле цифра.
- верная в узком смысле цифра.
Оставшиеся цифры числа 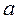 называют сомнительными.
называют сомнительными.
По умолчанию будем считать, что все значащие цифры числа 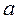 верны в узком смысле, т.е. его абсолютная погрешность не превосходит половины единицы последнего сохраненного разряда, например, запись
верны в узком смысле, т.е. его абсолютная погрешность не превосходит половины единицы последнего сохраненного разряда, например, запись 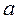 = 0,513 означает, что
= 0,513 означает, что 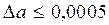 .
.
Результаты вычислений обычно округляют до верных знаков или оставляют одну сомнительную цифру. При округлении до верных знаков суммарная ошибка будет равна 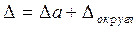 . Округляя числа, используют правило дополнения: если первая отбрасываемая цифра больше или равна 5, то последняя сохраненная цифра увеличивается на единицу.
. Округляя числа, используют правило дополнения: если первая отбрасываемая цифра больше или равна 5, то последняя сохраненная цифра увеличивается на единицу.
Задачи
1. Определить число значащих цифр в числах (устно):
4,15; 0,025; 0,005030; 238,06. Ответы: 3; 2; 4; 5.
2. Округлить до 3-х значащих цифр числа (устно):
0,08001; 1,0709; 0,6666; 123510; 3248,00.
Ответы: 0,0800; 1,07; 0,667; 124 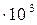 ; 325
; 325 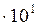 .
.
3. Определить число верных значащих цифр в числах (устно):
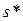 = 20,346
= 20,346 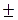 0,093;
0,093; 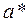 = 0,61
= 0,61 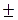 0,05;
0,05; 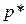 = 315
= 315 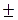 60.
60.
Решения:
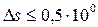 , следовательно, последняя верная цифра – 0;
, следовательно, последняя верная цифра – 0;
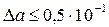 , значит, цифра 1 – сомнительная;
, значит, цифра 1 – сомнительная;
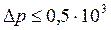 , значит, цифра 3 – сомнительная, в числе нет верных цифр. Ответы: 2; 1; 0.
, значит, цифра 3 – сомнительная, в числе нет верных цифр. Ответы: 2; 1; 0.
4. Округлить приближенные числа до верных знаков:
1) 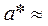 93;
93; 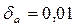 ; 2)
; 2) 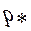
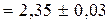 .
.
Решение. 1) 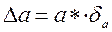 = 0,93 > 0,5; верная цифра может быть только одна. При округлении до одной значащей цифры суммарная ошибка будет
= 0,93 > 0,5; верная цифра может быть только одна. При округлении до одной значащей цифры суммарная ошибка будет 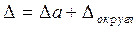 = 0,93 + 3 = 3,93 < 5.
= 0,93 + 3 = 3,93 < 5.
2) 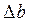 = 0,03 < 0,05. Суммарная ошибка при округлении до 2-х значащих цифр
= 0,03 < 0,05. Суммарная ошибка при округлении до 2-х значащих цифр 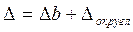 = 0,03+0,05 = 0,08 > 0,05. При округлении до одной значащей цифры
= 0,03+0,05 = 0,08 > 0,05. При округлении до одной значащей цифры 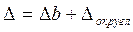 = 0,03 + 0,35 = 0,38 < 0,5. Ответы:
= 0,03 + 0,35 = 0,38 < 0,5. Ответы: 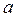 = 90;
= 90; 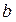 = 2.
= 2.
Задачи для самостоятельного решения
1. Округлить числа до верных знаков : 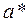
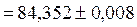 ;
;
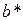
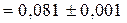 ;
; 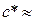 3,78,
3,78, 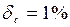 . Ответы: 84; 0,08; 4.
. Ответы: 84; 0,08; 4.
2. В результате измерения получены верные в написанных знаках числа: 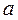 =
= 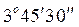 ;
; 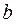 = 18,5 см;
= 18,5 см; 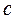 = 2,215 кг. Найти относительные погрешности этих чисел. Указание: число
= 2,215 кг. Найти относительные погрешности этих чисел. Указание: число 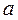 перевести в секунды.
перевести в секунды.
Ответы: 4 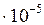 ; 0,003; 2
; 0,003; 2 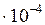
3. Какое из чисел определено более точно: 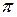 = 3,14 или
= 3,14 или 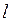 = 2567 ?
= 2567 ?
Указание: сравнить 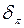 и
и 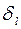 . Ответ:
. Ответ: 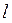 определено точнее.
определено точнее.
1.2 Погрешности арифметических операций
Основные формулы: 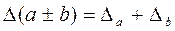 ;
;
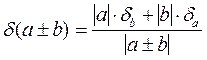 ;
; 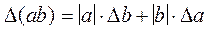 ;
;
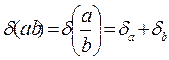 ;
; 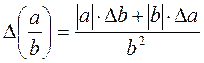 .
.
Следует запомнить:
1) при операциях сложения и вычитания суммируются абсолютные погрешности;
2) при умножении, делении суммируются относительные погрешности, при возведении в степень справедлива формула: 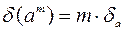 .
.
В практических вычислениях обычно используют следующее правило, основанное на приведенных выше формулах для погрешностей арифметических операций: при выполнении арифметических операций все промежуточные вычисления осуществляют с одной-двумя запасными цифрами по сравнению с желаемым результатом, а затем результат округляют:
- при сложении и вычитании - до наименьшего десятичного разряда в слагаемом с наибольшей абсолютной погрешностью;
- при умножении, делении и возведении в степень – до минимального количества значащих цифр в тех числах, с которыми оперировали.
Задачи
1. Найти относительную погрешность результата вычитания приближенных чисел: 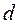 = 1,32 - 0,7.
= 1,32 - 0,7.
Решение. 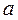 =
= 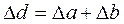 = 0,055;
= 0,055; 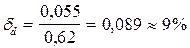 . Ответ:
. Ответ: 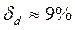 .
.
2. Сложить приближенные числа: 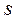 = 1,1732 + 217,45 + 0,0003 + 4,4.
= 1,1732 + 217,45 + 0,0003 + 4,4.
Решение. Округляем все числа до десятых плюс один знак и складываем их: 1,17
+217,45
0,00
4,4
 223,02
223,02
Ответ округляем до десятых (минимальное количество десятичных знаков после запятой было у числа 4,4). Ответ: 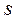 = 223,0.
= 223,0.
3. Вычислить произведение чисел 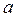 = 3,49 и
= 3,49 и 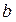 = 8,6 (записаны в верных знаках). Оценить погрешность результата и округлить его до верных цифр.
= 8,6 (записаны в верных знаках). Оценить погрешность результата и округлить его до верных цифр.
Решение. Вычисляем произведение с запасными знаками: 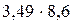 = 30,014. Погрешности:
= 30,014. Погрешности: 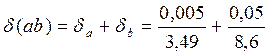 = 0,0014 + 0,0058 = 0,0072.
= 0,0014 + 0,0058 = 0,0072. 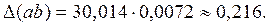 При округлении до 2-х значащих цифр ошибка D = 0,216 + 0,014 = 0,23 < 0,5, т.е. в ответе 2 верные значащие цифры. Ответ:
При округлении до 2-х значащих цифр ошибка D = 0,216 + 0,014 = 0,23 < 0,5, т.е. в ответе 2 верные значащие цифры. Ответ: 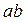 = 30.
= 30.
4. Выполнить деление приближенных чисел, если они записаны в верных знаках: 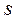 = 5,684 : 5,032 . Округлить результат до верных цифр.
= 5,684 : 5,032 . Округлить результат до верных цифр.
Решение. 
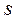
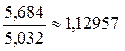 . Вычислим погрешности:
. Вычислим погрешности:
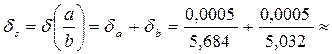 0,000088 + 0,000099 = 0,00019;
0,000088 + 0,000099 = 0,00019; 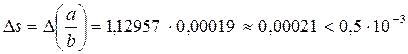 .
.
Округляем результат: 1,12957 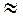 1,130. Суммарная ошибка
1,130. Суммарная ошибка 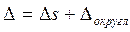 = 0,00021+0,00043 = 0,00064 > 0,0005. Еще раз округляем результат:
= 0,00021+0,00043 = 0,00064 > 0,0005. Еще раз округляем результат: 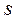 = 1,13. Суммарная ошибка
= 1,13. Суммарная ошибка 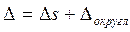 = 0,00064 < 0,005.
= 0,00064 < 0,005.
Ответ: 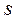 = 1,13.
= 1,13.
5. Вычислить 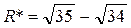 , оценить относительную погрешность результата. Ответ записать в верных цифрах.
, оценить относительную погрешность результата. Ответ записать в верных цифрах.
Решение. Вычислим корни с точностью до 0,001: 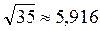 ;
; 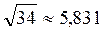 ;
; 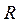 = 5,916 - 5,831 = 0,085.
= 5,916 - 5,831 = 0,085. 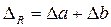
При округлении до десятых 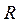 = 0,1;
= 0,1; 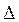 = 0,001+0,015 > 0,016 < 0,05. Ответ:
= 0,001+0,015 > 0,016 < 0,05. Ответ: 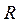 = 0,1
= 0,1
Сравним относительные погрешности слагаемых и результата.
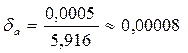 ,
, 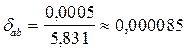 , но
, но 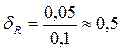 . Произошла большая потеря точности при вычитании близких чисел. Используем другой метод.
. Произошла большая потеря точности при вычитании близких чисел. Используем другой метод.
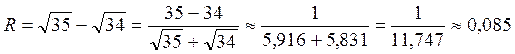 .
.
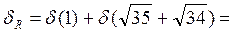
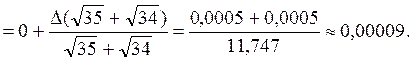
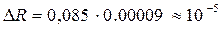 . В числе
. В числе 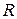 все цифры верные.
все цифры верные.
Ответ: 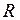 = 0,085.
= 0,085.
6. Вычислить 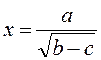 , если
, если 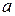 = 1,5;
= 1,5; 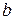 = 2,31;
= 2,31; 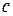 = 0,65 (числа записаны в верных знаках). Оценить погрешность результата.
= 0,65 (числа записаны в верных знаках). Оценить погрешность результата.
Решение. Вычислим x с запасными десятичными знаками:
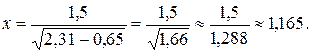 Погрешности:
Погрешности: 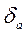
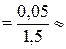 0,033;
0,033;
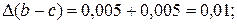
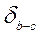
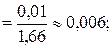
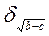 = 0,5
= 0,5 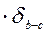 = 0,003;
= 0,003;
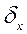 =
= 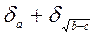 = 0,033 + 0,003 = 0, 036;
= 0,033 + 0,003 = 0, 036; 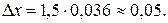
Ответ: 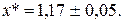
7. Вычислить 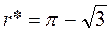 с точностью
с точностью 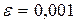 .
.
Решение. Результат должен удовлетворять условию: 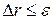 . Используем принцип равных влияний: вычислим слагаемые с одинаковой точностью, выбирая ее так, чтобы погрешность результата была не больше
. Используем принцип равных влияний: вычислим слагаемые с одинаковой точностью, выбирая ее так, чтобы погрешность результата была не больше 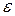 .
.
Если взять 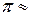 3, 142 и
3, 142 и 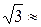 1,732,.
1,732,.
Задачи для самостоятельного решения
1. Вычислить 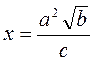 , если
, если 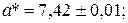
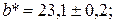
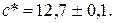 Оценить погрешность результата.
Оценить погрешность результата.
Ответ: 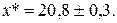
2. Даны два приближенных числа: 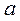 = 25,1;
= 25,1; 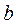 = 17,43. Вычислить
= 17,43. Вычислить 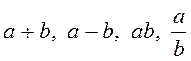 . Оценить погрешности результатов.
. Оценить погрешности результатов.
Ответы: 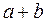 = 42,5;
= 42,5; 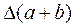 = 0,055;
= 0,055; 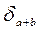 = 0,001;
= 0,001;
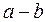 = 7,7;
= 7,7; 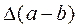 = 0,055;
= 0,055; 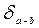 = 0,007;
= 0,007;
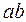 = 437;
= 437; 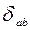 = 0,002;
= 0,002; 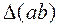 = 0,9;
= 0,9;
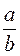 = 1,44;
= 1,44; 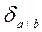 = 0,002;
= 0,002; 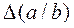 = 0,003.
= 0,003.
3. Вычислить 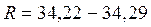 . Найти число верных знаков в ответе.
. Найти число верных знаков в ответе.
Ответ: 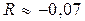 . Нет верных знаков.
. Нет верных знаков.
4. Вычислить 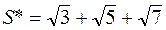 с точностью
с точностью 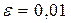 .
.
Ответ: 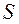 = 6,61.
= 6,61.
1.3 Погрешности вычисления значения функции
Если значение аргумента функции 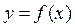 -приближенное число
-приближенное число 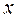 , то погрешность значения функции оценивают по формуле:
, то погрешность значения функции оценивают по формуле:
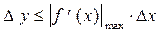 , где максимум производной - это ее наибольшее (по модулю) значение на промежутке
, где максимум производной - это ее наибольшее (по модулю) значение на промежутке 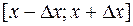 .
.
Погрешность значения функции 2-х аргументов 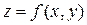 можно оценить формуле:
можно оценить формуле: 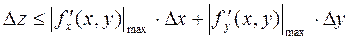 , где максимум частных производных находят среди всех значений в области
, где максимум частных производных находят среди всех значений в области
D = í(x,y)/ x-Dx £ x* £ x+Dx ; y-Dy £ y* £ y+Dyý.
Аналогично определяется погрешность значения функции n переменных 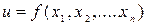 :
: 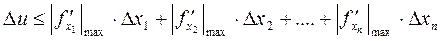 , где максимум частных производных находят среди всех значений в области
, где максимум частных производных находят среди всех значений в области
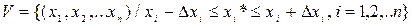 .
.
Задачи
1. Объем шара: 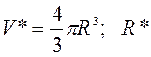 = 2,03
= 2,03 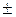 0,01. Найти
0,01. Найти 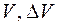 .
.
Решение. 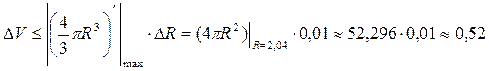 ;
; 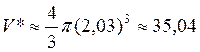 . Ответ:
. Ответ: 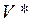 = 35,04
= 35,04 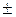 0,52.
0,52.
2. 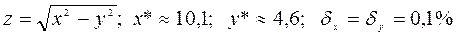 . Найти
. Найти 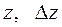 .
.
Решение. 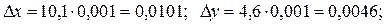
т.е. 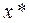 = 10,1
= 10,1 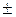 0,0101;
0,0101; 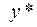 = 4,6
= 4,6 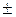 0,0046. Погрешность функции:
0,0046. Погрешность функции:
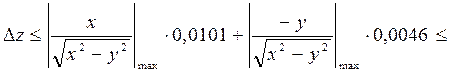
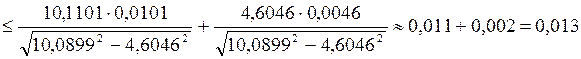 .
.
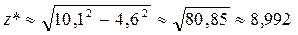 . Ответ:
. Ответ: 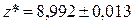 .
.
Задачи для самостоятельного решения
1. В прямоугольном треугольнике катет 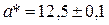 , гипотенуза
, гипотенуза 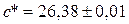 . Найти синус угла, лежащего напротив
. Найти синус угла, лежащего напротив 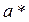 и оценить погрешность. Ответ:
и оценить погрешность. Ответ: 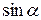
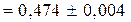 .
.
2. Период колебаний простого маятника 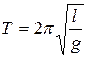 . Доказать, что
. Доказать, что 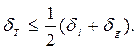
3. Вычислить удельный вес металла 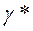 и оценить погрешность результата, если металлический цилиндр диаметром 2 см и высотой 11 см весит 93,4 г. Относительная погрешность измерения длин равна 0,01, а относительная погрешность взвешивания 0,001. Ответ:
и оценить погрешность результата, если металлический цилиндр диаметром 2 см и высотой 11 см весит 93,4 г. Относительная погрешность измерения длин равна 0,01, а относительная погрешность взвешивания 0,001. Ответ: 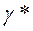 =2,70
=2,70 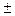 0,08.
0,08.
Литература:
[1], гл. I, работы №1, №2.
[3], гл X, §1 №3108 – 3124.
[4], т. I, гл. I, §1 – 4.
[5], гл. I, §1.1 – 1.10, упражнения к §1.
[6], гл. I, §1 – 5.
§2 Методы решения нелинейных уравнений
В этом параграфе рассматриваются методы решения нелинейных уравнений. В общем случае требуется найти решения уравнения 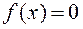 (или, иначе говоря, корень функции
(или, иначе говоря, корень функции 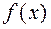 ), где
), где 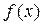 - нелинейная функция одной переменной. Все рассматриваемые в параграфе методы ориентированы на отыскание одного из возможных корней функции. Поэтому, если
- нелинейная функция одной переменной. Все рассматриваемые в параграфе методы ориентированы на отыскание одного из возможных корней функции. Поэтому, если 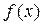 имеет более одного корня, то для отыскания каждого из них потребуется отдельное применение метода.
имеет более одного корня, то для отыскания каждого из них потребуется отдельное применение метода.
Использование каждого из методов вычислений предполагает, что известен отрезок 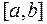 , внутри которого содержится хотя бы один корень функции. На практике определение такого отрезка часто требует отдельной процедуры и носит название этапа отделения или изоляции корня. Этот этап рассмотрен в первой части параграфа.
, внутри которого содержится хотя бы один корень функции. На практике определение такого отрезка часто требует отдельной процедуры и носит название этапа отделения или изоляции корня. Этот этап рассмотрен в первой части параграфа.
Полученный на этапе отделения корня отрезок 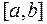 затем последовательно уменьшается и значение корня функции в результате определяется с требуемой точностью. Этот процесс носит название этапа уточнения корня. Именно он реализуется с помощью различных методов, называемых методами решения нелинейных уравнений и рассматриваемых в последующих частях параграфа.
затем последовательно уменьшается и значение корня функции в результате определяется с требуемой точностью. Этот процесс носит название этапа уточнения корня. Именно он реализуется с помощью различных методов, называемых методами решения нелинейных уравнений и рассматриваемых в последующих частях параграфа.
Для простоты в ходе дальнейшего изложения предполагается непрерывность функции 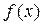 , что обеспечивает необходимые свойства большинства рассматриваемых в параграфе методов. Если требуются более жесткие условия на функцию, то они оговариваются особо.
, что обеспечивает необходимые свойства большинства рассматриваемых в параграфе методов. Если требуются более жесткие условия на функцию, то они оговариваются особо.
2.1 Изоляция корней
Пусть функция 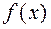 непрерывна в области определения. Чтобы гарантированно существовало решение уравнения
непрерывна в области определения. Чтобы гарантированно существовало решение уравнения 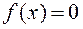 (1), функция должна быть знакопеременной в области определения. Процедура нахождения промежутка
(1), функция должна быть знакопеременной в области определения. Процедура нахождения промежутка 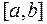 , внутри которого обязательно находится корень функции, называется, как уже отмечалось, этапом отделения корня или его изоляцией. Отделение корней может быть осуществлено численно или графически.
, внутри которого обязательно находится корень функции, называется, как уже отмечалось, этапом отделения корня или его изоляцией. Отделение корней может быть осуществлено численно или графически.
Численная процедура отделения корня, как правило, сводится к определению знака функции на некотором дискретном множестве значений аргумента. Чаще всего это множество представляет собой конечный набор равноотстоящих точек на оси абсцисс. При реализации этой процедуры руководствуются следующими правилами:
1) Если 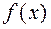 непрерывна на
непрерывна на 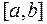 и
и 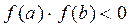 , то существует хотя бы один корень
, то существует хотя бы один корень 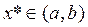 .
.
2) Если 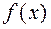 непрерывна и монотонна на
непрерывна и монотонна на 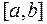 , причем
, причем 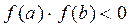 , то корень
, то корень 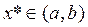 единственный.
единственный.
Следует отметить, что случаи, когда функция в отдельных точках принимает значения, равные нулю, а в остальных точках области определения сохраняет знак, этими правилами не отслеживаются.
Задачи
1. Найти промежутки изоляции корней уравнения 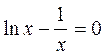 .
.
Решение. Функция 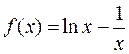 непрерывна и монотонна на всей области определения
непрерывна и монотонна на всей области определения 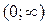 , т.к.
, т.к. 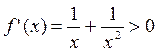 , следовательно, уравнение имеет не более одного решения. Подбираем точки
, следовательно, уравнение имеет не более одного решения. Подбираем точки 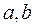 , такие, что
, такие, что 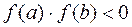 .
.
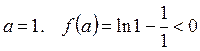 .
. 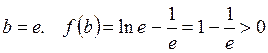 .
.
Ответ: 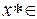 [1; e].
[1; e].
2. Найти промежутки изоляции решения уравнений, используя графический метод:  .
.
|
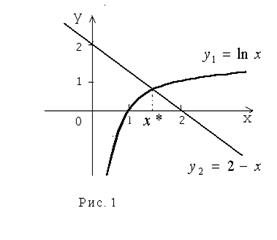
Решение. 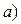 Запишем уравнение в виде
Запишем уравнение в виде 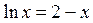 и построим графики функций
и построим графики функций 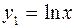 и
и 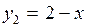 . Абсциссы точек пересечения графиков (
. Абсциссы точек пересечения графиков ( 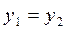 ) равны корням функции
) равны корням функции 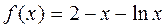 . Из графика видно, что
. Из графика видно, что 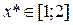 .
.
Проверка: 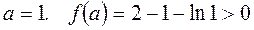 .
. 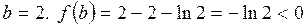 Ответ:
Ответ: 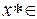
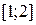 .
.
|
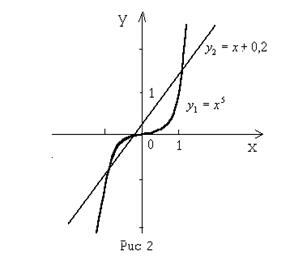
 Запишем уравнение в виде
Запишем уравнение в виде 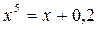 и построим графики функций
и построим графики функций 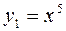 и
и 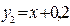 . Как видно из графика, линии пересекаются в трех точках:
. Как видно из графика, линии пересекаются в трех точках:
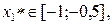
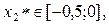
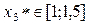 .
.
Проверка. 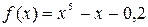 .
.
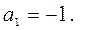
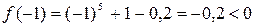
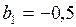
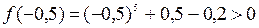
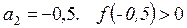 .
. 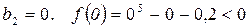 .
.
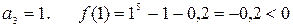
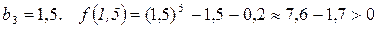 .
.
Ответ: 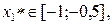
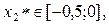
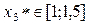 .
.
Задачи для самостоятельного решения
Найти промежутки изоляции корней для следующих уравнений: 
1). 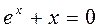 . 2).
. 2). 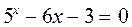 . 3).
. 3). 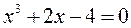
Ответы: 1) [-1; 0]; 2) [-1; 0] и [1; 2]; 3) [1; 2].
Дата добавления: 2021-07-22; просмотров: 509;











