Цепь с последовательным соединением активного сопротивления индуктивности и емкости. Резонанс напряжений.

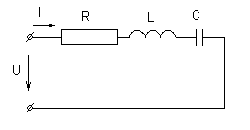
i = I_M sinWt

u = u_R + u_L + u_C

Рассмотрим 3 случая:

1) U_L > U_C ; X_L > X_C

2) U_L < U_C : X_L < X_C

3) U_L = U_C : X_L = X_C

1 случай U_L > U_C ; X_L > X_C .

;
;

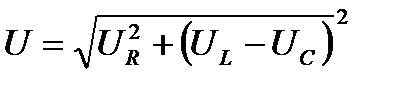
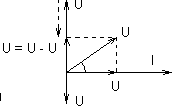
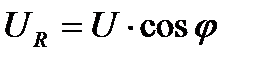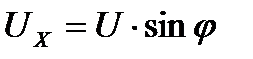
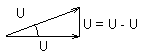
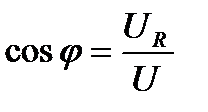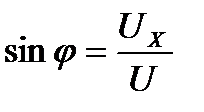
Умножив каждую сторону на ток, получим треугольник мощностей.

,

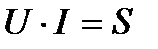
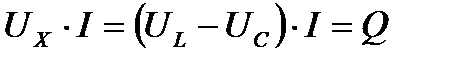
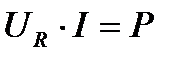
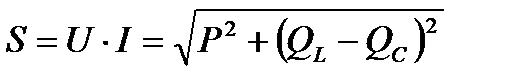
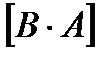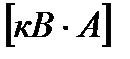
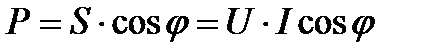
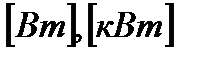
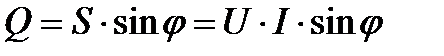
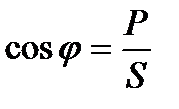
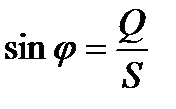
Коэффициент мощности 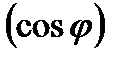показывает, какую долю от полной мощности составляет активная мощность.

Разделив каждую сторону треугольника напряжений на ток, получим треугольник сопротивлений.

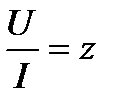
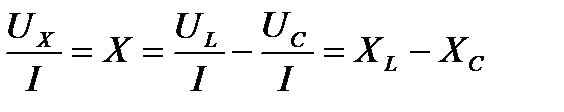
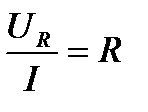
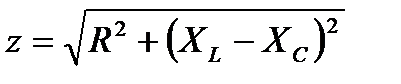- полное сопротивление цепи

,

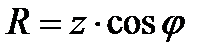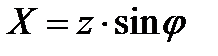
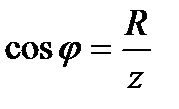
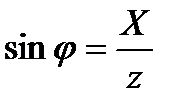
2-й случай U_L < U_C , X_L < X_C

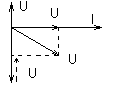
Все остальное, в принципе то же самое.

3-й случай: U_L = U_C : X_L = X_C

В последовательной цепи, состоящей из активного сопротивления, индуктивности и емкости, при равенстве реактивных сопротивлений X_L и X_C резонанс напряжений.

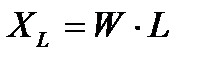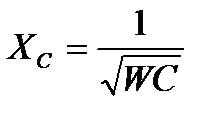Т.к. а , то при резонансе 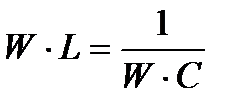или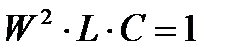

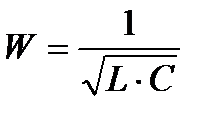- угловая скорость

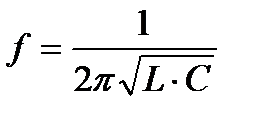- частота

Установлено, что в контуре без потерь, подключенном к источнику постоянного напряжения, возникает переменный ток с угловой частотой собственных колебаний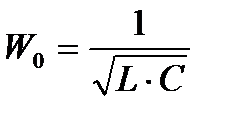

Т.е резонанс наступает, если частота напряжения источника питания W совпадает с частотой собственных колебаний контура W₀, при этом X=X_L-X_C=0 т.е реактивное сопротивление равно нулю.

При резонансе сопротивление любого из реактивных участков цепи:

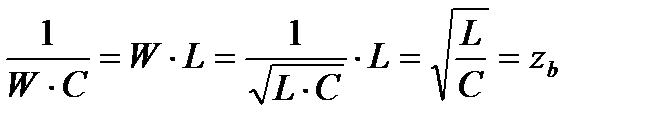
Принято называть волновым сопротивлением.

Величина 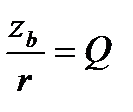- называется добротностью контура.

Полное сопротивление цепи при резонансе напряжений:

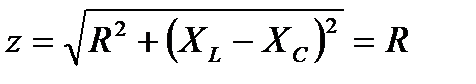
Равно активному сопротивлению цепи, и следовательно, наименьшее из всех возможных при изменении частоты f.

Ток в цепи (действующее значение) при резонансе достигает максимума и совпадает с напряжением по фазе.

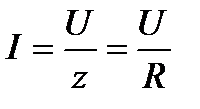
При резонансе индуктивное напряжение 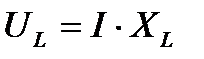и емкостное 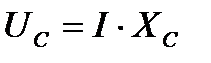, сдвинутые по фазе на половину периода, равны по величине;

Напряжение на зажимах цепи U равно активному напряжению .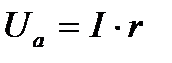

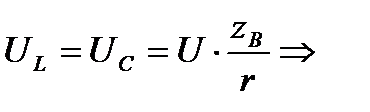при z_B > R напряжение U_L и U_C больше приложенного к зажимам цепи!

Настройка цепи в зажим резонанса напряжений может быть выполнена следующим образом:

1) при неизменной индуктивности изменением емкости

2) при неизменной емкости изменением индуктивности

3) при неизменной емкости и индуктивности изменением частоты.