Уравнение Клайперона 1834г.

Техническая термодинамика. Основные понятия и определения.

Термодинамика изучает законы превращения энергии в различных процессах, происходящих в макроскопических системах, и сопровождается тепловыми эффектами (макроскопическая система- это объект, который состоит из большого числа частиц). Техническая термодинамика изучает закономерности взаимного превращения тепловой и механической энергии и свойства тел, участвующих при этом вращении.

Вместе с теорией теплообмена она является теоретическим фундаментом теплотехники.

Термодинамическая система представляет собой совокупность материальных тел, находящихся в механическом и тепловом взаимодействии друг с другом и с окружающим систему внешними телами (внешней средой).

Сведения по физике

Основные параметры: температура, давление и удельный объем.

Под температурой понимают физическую величину, характеризующую степень нагретости тела. Применяют 2 температурные шкалы: термодинамическую Т(°К) и международную практическую t (°С). Соотношение между Т и t определяется по значениям тройной точки воды:

Т= t(°С)+273,15

Тройная точка воды – состояние, при котором твердое, жидкое и газообразное фазы находятся в равновесии.

За единицу давления принимается Паскаль (Па) данная единица очень мала, поэтому используют большие величины кПа, МПа. А также внесистемные единицы измерения – техническая атмосфера и миллиметры ртутного столба. (мм.рт.ст.)

Рн =760мм.рт.ст.=101325 Па=101,325 кПа = 0,1 МПА=1кг/см

Основные параметры состояния газа связаны между собой уравнением:

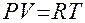
Уравнение Клайперона 1834г.

R- Удельная газовая постоянная.

Умножив левую и правую части на m, получим уравнение Менделеева, Клайперона, где m- молекулярная масса вещества:

m×R×u=R×T×m

Значение произведения m× R называют универсальной газовой постоянной, её выражение определяется из формулы:

m×R=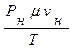

При нормальных физических условиях: 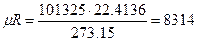Дж/(Кмоль*К).

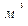Где m×Vн=22,4136 /Кмоль - молярный объем идеального газа при нормальных физических условиях.

Удельная газовая постоянная R- это работа, затраченная на нагревание 1 кг вещества на 1 К при постоянном давлении

R= ,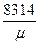

Если все термодинамические параметры постоянны во времени и одинаковы во всех точках системы, то такое состояние системы называется равновесным. Если между различными точками в системе существуют разности температур, давлений и других параметров, то она является неравновесной. В такой системе под действием градиентов параметров возникают потоки теплоты, вещества и другие, стремящиеся вернуть её в состояние равновесия. Опыт показывает, что изолированная система с течением времени всегда приходит в состояние равновесия и никогда самопроизвольно выйти из него не может. В классической термодинамике рассматривается только равновесные системы т.е.:

В реальных газах, в отличие от идеальных, существуют силы межмолекулярных взаимодействий (силы притяжений, когда молекулы находятся на значительном расстоянии и силы отталкивания, когда молекулы отталкиваются). И нельзя пренебречь собственным объемом молекул. Для равновесной термодинамической системы существует функциональная связь между параметрами состояния, которое называется уравнением состояния.

Опыт показывает, что удельный объем, температура и давление простейших систем, которыми являются газы, пары или жидкости связаны термическим уравнением состояния вида:

f r,u,T)=0

Уравнения состояния реальных газов.

Наличие межмолекулярных сил отталкивания приводят к тому, что молекулы могут сближаться между собой до некоторого минимального расстояния. Поэтому можно считать, что свободные для движения молекул, объем будет равен:

u-b;

где b- тот наименьший объем, до которого можно сжать газ.

В соответствии с этим длина свободного пробега уменьшается и число ударов о стенку в единицу времени, а следовательно давление увеличивается.

, ,

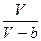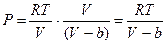Возникает молекулярное (внутреннее) давление.

Сила молекулярного притяжения каких-либо 2 малых частей газа пропорциональна произведению числа молекул в каждой из этих частей, т.е. квадрату плотности, поэтому молекулярное давление обратнопропорционально квадрату удельного объема газов: Рмол £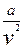

Где а - коэффициент пропорциональности, зависящий от природы газов.

Отсюда уравнение Ван-дер-Ваальса (1873г.)

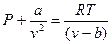
При больших удельных объемах и сравнительно невысоких давлениях реального газа уравнение Ван-дер-Ваальса практически выражается в уравнение состояния идеального газа Клайперона. Ибо величина 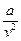(по равнению с Р) и b по сравнению с u становятся пренебрежимо малыми.