Первый закон термодинамики.

Первый закон термодинамики является частным случаем общего закона сохранения энергии: «Энергия не создается из ничего и не исчезает бесследно, а превращается из одной формы в другую в строго определенных количествах» (Ломоносов).

В результате подвода теплоты тело нагревается (dt>0) и увеличивается его объем, поэтому увеличение объема связано с наличием внешней работы:

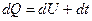или Q=DU+ L

Где Q- общее количество тепла, приведенного к системе.

DU- изменение внутренней энергии.

L-работа, направленная на изменение объема термодинамической системы.

Теплота, сообщаемая термодинамической системе идет на увеличение внутренней энергии и на совершение внешней работы.

Первый закон:

«невозможно создать машину производящую работу без того чтобы эквивалентное количество энергии другого вида не исчезала» (Вечный двигатель первого рода)

То есть невозможно построить двигатель, который вырабатывал бы энергию из ничего. Иначе вырабатывал бы энергия не потребляя при этом какую-либо другую энергию.

Теплоемкость.

Для того чтобы повысить температуру любого вещества, необходимо подвести определенное количество теплоты. Выражение истинной теплоемкости:

,

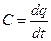Где 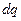- элементарное количество теплоты.

dt – соответствующие изменения температуры вещества в данном процессе.

Выражение показывает удельную теплоемкость, то есть количество теплоты необходимое подвести единице количества вещества для нагревания его на 1 К (или 1 °С). Различают массовую теплоёмкость (С) отнесенную к 1 кг. Вещества, необходимую (С’) отнесенную к 1 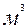вещества и киломольную (mС) отнесенную к 1 кмолю.

Удельная теплоемкость – это отношение теплоемкость тела к его массе:

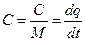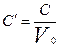; - объемная.

Процессы с подводом теплоты при постоянном давлении называется изобарными, а с подводом теплоты при постоянном объеме – изохорным.

При теплотехнических расчетах в зависимости от процессов теплоемкости получают соответствующие названия:

Сv- изохорная теплоемкость,

Ср- изобарная теплоемкость.

Теплоемкость при изобарном процессе (p=const)

,

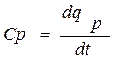При изохорном процессе:

,

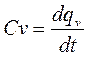Уравнение Майера:

Ср-Сv=R - показывает связь между изобарным и изохорным процессами.

В процессах V=const работа не совершается а полностью расходуется на изменение внутренней энергии dq=dU , при изобарном подворье теплоты имеет месть увеличение внутренней энергии и совершение работы против внешних сил, поэтому изобарная теплоемкость Ср всегда больше изохорной на величину газовой постоянной R.

Энтальпия

В термодинамике важную роль играет сумма внутренней энергии системы U и произведения давления системы р на её объем V, называемая энтальпией и обозначается Н.

Н=U+pV,

Т.к. входящие в нее величины являются функциями состояния, то и сама энтальпия является функцией состояния, также как и внутренняя энергия, работа и теплота она измеряется в Дж.

Удельная энтальпия h=H/M представляет собой энтальпию системы, содержащей 1 кг вещества, и измеряется в Дж/кг. Изменение энтальпии в любом процессе определяется только начальным и конечным состояниями тела и не зависит от характер процесса.

Физический смысл энтальпии выясним на примере:

Рассмотрим расширенную систему, включающую газ в цилиндре и поршень с грузом, общим весом G. Энергия этой системы складывается из внутренней энергии газа и потенциальной энергии поршня с грузом.

E=U+Gy;

В условиях равновесия G=pF эту функцию можно выразить через параметры газа:

E=U+p∙F_У;

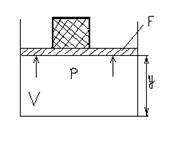
Получаем, что ЕºН, т.е. энтальпию можно трактовать как энергию расширенной системы. Если давление системы сохраняется независимым, т.е. осуществляется изобарный процесс dp=0, то q_P = h₂ - h₁, т.е. теплота, подведенная к системе при постоянном давлении, идет только на измерение энтальпии данной системы. Это выражение очень часто используется в расчетах, так как огромное количество процессов подводов теплоты в термодинамике (в паровых котлах, камерах сгорания газовых турбин и реактивных двигателей, теплообменных аппаратах) осуществляется при постоянном давлении. При расчетах практический интерес представляет изменение энтальпии в конечном процессе:

;

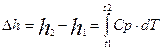Энтропия

Название энтропия происходит от греческого слова «энтропос»- что означает превращение, обозначается буквой S, измеряется [Дж/К], а удельная энтропия [Дж/кг×К]. В технической термодинамике является функцией, которая характеризует состояние рабочего тела, следовательно является функцией состояния: ,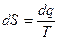

где 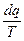- полный дифференциал некоторой функции состояния.

Формула применима для определения изменения энтропии, как идеальных газов, так и реальных может быть представлен в виде зависимости от параметров:

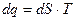
Это означает, что элементарное количество подведенной (отведенной) удельной теплоты в равновесных процессах равно произведению термодинамической температуры на изменение удельной энтропии.

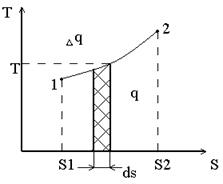
Понятие энтропии позволяет ввести чрезвычайно удобную для термодинамических расчетов TS - диаграмму, на которой, как и на PV- диаграмме состояние термодинамической системы изображается точкой, а равновесный термодинамический процесс линией

Dq - Элементарное количество теплоты.

;

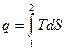Очевидно, что в TS-диаграмме элементарная теплота процесса изображается элементарной площадкой с высотой Т и основанием dS, а площадь, ограниченная линиями процесса, крайними ординатами и осью абсцисс, эквивалентна теплоте процесса.

Если Dq>0, то dS>0

Если Dq<0, то dS<0 (отвод теплоты).