ЗАВИСИМОСТЬ МЕЖДУ КООРДИНАТАМИ ТОЧКИ ГОРИЗОНТАЛЬНОГО И НАКЛОННОГО СНИМКОВ.

В фотограмметрии часто применяются зависимости между координатами точек горизонтального и наклонного снимков. Их легко получить из уравнений (28) и (34), с учетом того, что Z_S – Z = H и координаты главной точки равны нулю. Левые части этих уравнений выражают одни и те же величины – координаты X и Y точки местности. Поэтому справедливо:

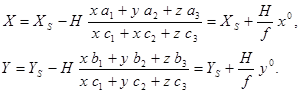
Откуда

(40)

Таким образом, если даны его угловые элементы внешнего ориентирования, то по формулам (40) можно перейти от координат точек на наклонном снимке, к координатам соответствующих точек на горизонтальном снимке. Этот процесс называется трансформированием координат. Они справедливы при любых значениях угловых элементов внешнего ориентирования снимка.

Подставив в уравнения (40) выражения направляющих косинусов из (21), после преобразований с точностью до членов второго порядка малости получим:

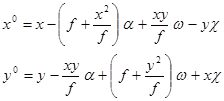
(41)

Приведенные формулы проще, но они перестали быть строгими.

Строгие и простые соотношения можно написать, если начало координат на снимке и на местности совместить с точкой нулевых искажений с, тогда с учетом уравнений (34) и(38) получим:

,

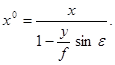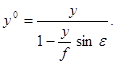
(42)

МАСШТАБ СНИМКА.

Масштабом снимка 1/m в данной точке по данному направлению называется отношение бесконечно малого отрезка dl на снимке к соответствующему отрезку dL на местности. То есть:

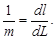
(43)

Пусть местность равнинная, а начала координат в пространстве и на снимке расположены соответственно в точках S и o,(рис. 32).

Обозначив проекции отрезков dl и dL на соответствующие координатные оси через dx, dy и dX, dY, с учетом данного определения масштаба и рис. 32 напишем:

,

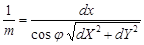(44)

где φ – угол между осью x снимка и заданным направлением отрезка dl.

При указанном выборе систем координат, и при условии, что оси ординат расположены в плоскости главного вертикала, справедливы уравнения (37) зависимости между координатами точек местности и снимка. Продифференцируем их по переменным x и y, в результате получим:

.

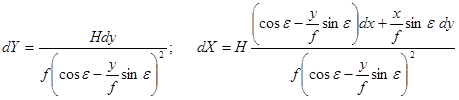Введём обозначение:

.

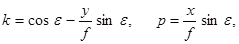и учтем, что dy=dxtgj, тогда

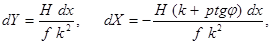
(45)

Подставив выражения dX и dY из соотношений (45) в формулу (44), будем иметь:

.

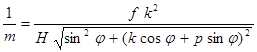(46)

Полученное равенство показывает, что масштаб снимка зависит от фокусного расстояния АФА, высоты фотографирования, угла наклона снимка, положения точки на снимке (координат x и y), в которой взят элемент dl и от направления φ этого элемента относительно линии главного вертикала .

Определим значение масштаба 1/m для частных случаев.

1. Масштаб горизонтального снимка (ε = 0). Подставив это значение в формулу (46), с учетом принятых обозначений k и p получим:

,

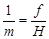т. е. масштаб горизонтального снимка плоской местности во всех точках постоянный.

2. Масштаб наклонного снимка по направлению главной вертикали (x = 0, φ = 90°):

.

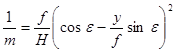(47)

На основании уравнения (47) запишем значение масштаба 1/m в характерных точках, лежащих на линии главного вертикала:

В главной точке снимка o (y = 0)

;

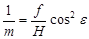В точке нулевых искажений с , поэтому:

;

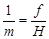В точке надира n 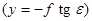, после подстановки получаем:

;

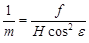В главной точке схода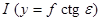

.

Таким образом, масштаб в точке нулевых искажений равен, в главной точке мельче, а в точке надира крупнее масштаба горизонтального снимка. Масштаб в точке нулевых искажений называется главным масштабом снимка.

3. Масштаб наклонного снимка по направлению горизонтали (φ = 0°)

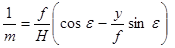
(48)

Поскольку в уравнении абсцисса точки отсутствует, то вдоль горизонтали, если местность равнинная, мосштаб величина постоянная.

Запишем выражения 1/m для горизонталей, проходящих через характерные точки снимка:

По линии действительного горизонта 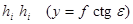, поэтому:

;

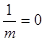Вдоль главной горизонтали 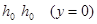, после подстановки имеем:

;

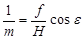На линии неискажённого масштаба 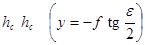, значит

;

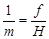По горизонтали h_nh_n, проходящей через точку надира 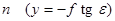, и:

.

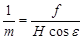Выполненный анализ показал, что масштаб снимка в точке c по любому направлению равен масштабу горизонтального снимка.