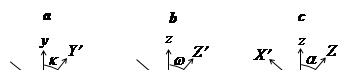ЗАВИСИМОСТЬ МЕЖДУ ПРОСТРАНСТВЕННЫМИ И ПЛОСКИМИ КООРДИНАТАМИ ТОЧКИ СНИМКА.

При изучении теории фотограмметрии и решении практических задач используются зависимости между плоскими координатами x, y точек снимка и их пространственными координатами X', Y', Z'. Эти зависимости можно установить, если известны элементы внутреннего и угловые элементы внешнего ориентирования снимка.

Введём для этого систему координат S x y z с началом в точке фотографирования S (рис. 29). Координатные оси x, y этой системы расположим параллельно соответствующим осям на снимке, а ось z совместим с главным лучом связки So. Тогда координаты x, y любой точки снимка в пространственной системе имеют те же значения, что и в плоской, а координата z для всех точек постоянна и равна фокусному расстоянию снимка (z = -f).

Системы S X' Y' Z' и S x y z имеют общее начало, поэтому в процессе преобразования координат из одной сиситемы в другую следует выполнять только вращение, что выражается, например, формулой:

.

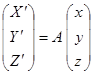(14)

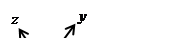Ортогональная матрица А имеет третий порядок и называется матрицей преобразования координат. Ее элементами являются 9 направляющих косинуса, поэтому выше приведенное соотношение можно записать и так:

.

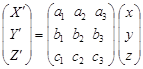(15)

Причем, каждый из направляющих косинусов это косину угла между соответствующими осями систем координат участвующих в преобразовании, то есть:

;

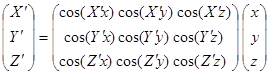(16)

Отметим, что в формуле 16 не произведения координат, заключенных в скобках, а обозначение осей, между которыми берется угол.

В силу ортогональности направляющие косинусы матрицы связаны между собой шестью независимыми уравнениями:

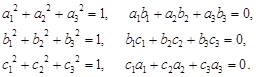
(17)

Один поворот в пространстве можно заменить тремя последовательными поворотами в плоскости (вокруг осей Z, X и Y, рис.30). Им будут соответствовать матрицы 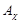, А_ω, и А_α.. В соответствии с рис. 26 для каждого из поворотов соотношение 16 можно представить следующим образом:

, ,

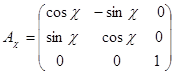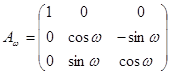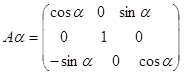
Общая матрица преобразования A равна произведению:

А = А_α А_ω

После перемножения матриц и получим формулы для вычисления направляющих косинусов. В данном случае они будут иметь вид:

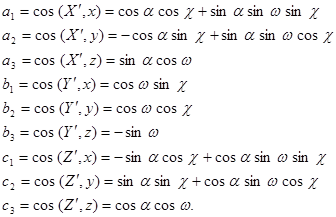
(18)

Таким образом, направляющие косинусы а₁, а₂, а₃,…..,с₃ зависят от трёх угловых элементов внешнего ориентирования снимка и являются координатами единичных векторов, определяющих взаимное положение рассматриваемых систем координат: X' Y' Z' и x y z.

Аналогично для второй группы элементов внешнего ориентирования снимка можно получить:

Формулы (18) и (19) позволяют установить связь между элементами ориентирования и направляющими косинусами разных систем ЭВО:

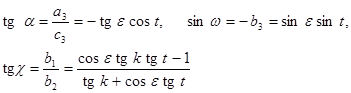
Можно было бы привести и еще ряд соотношений.

Переход от пространственных координат к плоским осуществляется по формулам:

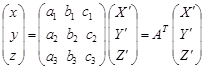
(20)

где А^Т – транспонированная матрица А.

Если начало координат снимка не совпадает с его главной точкой, то вместо координат x и y в формулах 14,15,16 и 20 следует использовать разности x – x_о и y - y_о.

Формулы (14) – (20) справедливы для любых значений угловых элементов внешнего ориентирования снимка.

Для плановых снимков, когда α, ω и 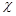малы, с точностью до членов второго порядка малости можно записать:

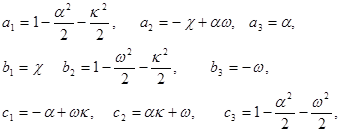
(21)

Если же учитывать только члены первого порядка малости, то:

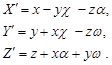
(22)

Для случая, изображенного на рис. 29 матрица A будет единичной, то есть:

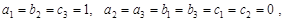
(23)

Полученные зависимости между системами координат X' Y' Z' и x y z используются в аналитических способах определения координат точек местности по измерениям снимков.