ЗАВИСИМОСТЬ МЕЖДУ КООРДИНАТАМИ ТОЧКИ МЕСТНОСТИ И СНИМКА

Точка местности М и её изображение на снимке т находятся на одном проектирующем луче (рис.31). Положение точек S и М в системе координат местности X Y Z определяется векторами соответственно 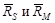, а положение точек т и М в системе координат S X' Y' Z' – векторами .

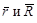Векторы 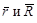коллинеарны, поэтому

,

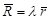(24)

где λ – скаляр, а

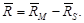
Спроектируем векторы 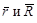на координатные оси X, Y, Z, тогда:

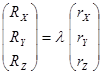
(25)

Из третьего равенства (25) найдем λ и подставим его выражение в первое и второе. Тогда:

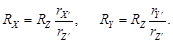
(26)

Так как

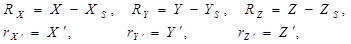
то

,

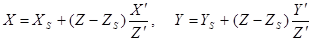(27)

Или, с учётом равенства (15)

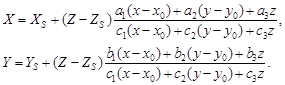
((28)

Итак, если элементы ориентирования снимка даны, то два уравнения (27) имеют три неизвестных. Отсюда следует, что пространственные координаты точки местности по одиночному снимку не определить. Можно получить лишь ее плановое положение. Но надо знать высоту фотографирования H = - (Z – Z_S).

В фотограмметрии часто используются обратные зависимости (между координатами точки снимка и координатами соответствующей точки местности). Для их получения, спроектируем векторы 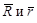равенства (24) на координатные оси системы координат S x y z (рис. 31), в результате получим:

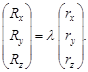
(29)

Решим третье уравнение относительно λ и подставим его значение в первое и второе уравнения. Тогда:

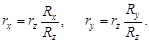
(30)

Матрицы-столбцы равенств (29) можно представить в виде:

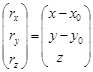;	((31)
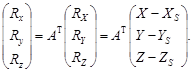
	((32)

Подставив выражения проекций векторов r и R из (31) и (32) в (30), будем иметь:

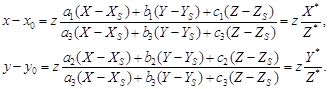
(33)

Формулы (28) и (33) справедливы при любых значениях элементов ориентирования снимка.

Пусть x₀ = y₀ = 0, X_S = Y_S = 0, Z_S – Z = H, тогда при условии расположения осей как на рис. 24 (снимок можно считать горизонтальным) формулы (28) и (33) будут выглядеть следующим образом:

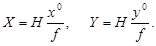
	(34)
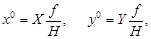
	(35)

где x⁰, y⁰ – координаты точки горизонтального снимка.

Предположим теперь, что снимок наклонный, но при этом 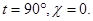Матрица преобразования координат A будет иметь вид:

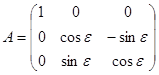
(36)

И при указанных выше условиях (x₀ = y₀ = 0, X_S = Y_S = 0, Z_S – Z = H), получим:

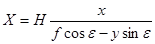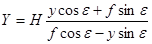и (37)

Уравнения (37) записаны для случая, когда начало координат на местности совмещено с точкой S или N, а на снимке - с главной точкой о. Если же начала координат перенести соответственно в точки C и c, то соотношения станут еще более простыми:

,

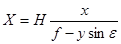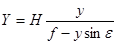
(38)

При условии, что за начало координат на местности принята точка N, а на снимке – соответствующая ей точка надира n, справедливы следующие соотношения;

,

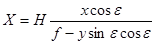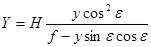
(39)

Уравнения (38) и (39) легко получить из соотношения 37 и переносом систем координат на снимке и в пространстве.