Уравнение состояния идеального газа

Равновесное состояние идеального газа как термодинамической системы определяется его параметрами: температурой T, давлением p и удельным объемом 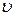. Между этими параметрами существует связь, которая выражается уравнением состояния. Уравнение состояния идеального газа имеет вид:

.

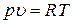(2)

Здесь R – газовая постоянная, ;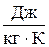

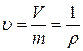– удельный объем вещества.

Это уравнение записано для массы идеального газа, равной 1 кг, и носит название уравнения Клапейрона.

Для одного киломоля газа уравнение (2) запишется так:

,

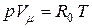(3)

где V_μ – объем одного киломоля газа при данных условиях, R₀ – универсальная газовая постоянная, одинаковая для одного киломоля любого газа:

.

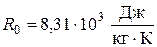Для произвольной массы газа m с молекулярной массой μ уравнение (3) запишется в виде

,

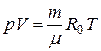(4)

где V – объем, занимаемый m кг газа, 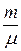– число киломолей газа.

Уравнение (4) можно записать также в виде

.

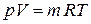(5)

Газовая постоянная R связана с универсальной газовой постоянной R₀ соотношением

.

(6)

Уравнения (2) и (5) называются характеристическими, поскольку с их помощью можно характеризовать состояние идеального газа.

Смесь газов

В природе и в технике очень часто встречаются различные смеси газов. Например, воздух представляет собой смесь газов (азот, кислород, углекислый газ и др.), различные горючие газы, представляют собой смесь углеводородов (пропана, бутана, метана, пентана и др.), продукты горения, состоят из смеси газов (углекислый газ, азот, окись углерода и др.).

Поэтому важно понять закономерности, которым подчиняются смеси газов.

Если различные компоненты газовой смеси не вступают между собой в химические реакции, то каждый газ равномерно распределяется по всему объему сосуда. Давление, которое оказывает каждый газ в смеси, называется парциальным. То есть, парциальное давление газа в смеси равно давлению, которое будет, если этот газ один занимает весь объём смеси при той же температуре. Его можно определить по температуре и объему смеси на основании характеристического уравнения (5) для данного газа.

По закону Дальтона, давление, оказываемое смесью газов, равно сумме парциальных давлений отдельных газов, входящих в состав смеси:

.

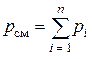Смесь газов ведет себя как однородный газ и его состояние можно описать характеристическими уравнениями

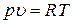
	– для одного килограмма газовой смеси;
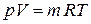
	– для m кг смеси;
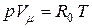
	– для одного киломоля смеси.

Однако для использования этих уравнений необходимо знать газовую постоянную смеси либо молекулярную массу смеси, связанную с газовой постоянной соотношением

.

Эти величины зависят от количественного и качественного состава газовой смеси. При этом состав смеси может быть задан в массовых или объемных долях.

Массовая доля представляет собой отношение массы компонента к массе всей смеси:

.

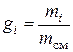Объемная доля представляет собой отношение объема компоненты смеси при давлении смеси к объему всей смеси:

.

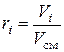Чтобы применить уравнение Клапейрона для смеси идеальных газов необходимо вычислить газовую постоянную смеси R_см или молекулярную массу смеси μ_см.

Существуют два способа расчета этих величин: массовый и объемный.

Если задан массовый состав смеси, то есть, заданы массовые доли каждого газа в смеси, тогда

.

.

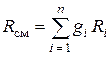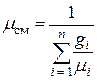Если задан объемный состав смеси, то есть, заданы объемные доли каждого газа в смеси, тогда

.

.

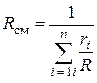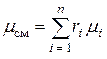Массовые и объемные доли связаны между собой

.

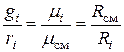После определения R_см и μ_см смесь можно рассматривать как однородный газ с соответствующими характеристиками.