Основные термодинамические процессы
Изучение термодинамического процесса заключается в определении работы, совершаемой газом в этом процессе, изменения внутренней энергии, количества теплоты и установлении прочих связей между параметрами термодинамического процесса.
Рассмотрим закономерности изменения параметров для основных термодинамических процессов.
Изохорный процесс
Изохорным называют термодинамический процесс, протекающий при постоянном объеме.
Количественные характеристики изохорного процесса можно получить из уравнения состояния
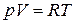 ,
,
откуда
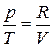 .
.
Поскольку в изохорном процессе V = const, то
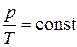 и и 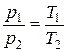 , ,
| (13) |
то есть, давление, оказываемое газом на стенки сосуда, при изохорном процессе пропорционально температуре (закон Шарля). Зависимости (13) есть уравнения изохорного процесса.
На p – V диаграмме изохорный процесс отобразится прямой линией, параллельной оси ординат, называемой изохорой (рис. 6).
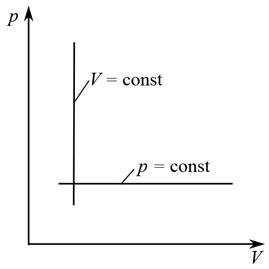
Рис. 6
Так как при изохорном процессе 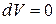 , то и
, то и 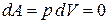 , то есть не совершается никакой работы по преодолению внешних сил. Тогда первый закон термодинамики запишется как
, то есть не совершается никакой работы по преодолению внешних сил. Тогда первый закон термодинамики запишется как
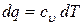 ,
,
то есть вся подведенная теплота расходуется на увеличение внутренней энергии (температуры) газа.
Изобарный процесс
Изобарным называют термодинамический процесс, протекающий при постоянном давлении. Первый закон термодинамики для этого процесса будет иметь вид
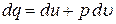
или
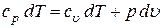 .
.
Из характеристического уравнения при постоянном давлении получим
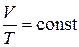 или или  , ,
| (14) |
то есть, при изобарном процессе объем, занимаемый массой газа, прямо пропорционален температуре (закон Гей-Люссака). Графически изобарный процесс отобразится прямой линией, параллельной оси абсцисс – изобарой (рис. 6).
Для одного килограмма газа при изобарном процессе можно записать:
· количество подведенного тепла 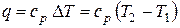 ;
;
· изменение внутренней энергии 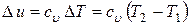 ;
;
· работа по преодолению внешних сил 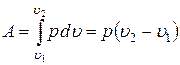 .
.
На основании характеристического уравнения (уравнения состояния) 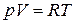 можно записать
можно записать
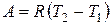 .
.
Можно оценить, какая приблизительно часть подводимой тепловой энергии при изобарном процессе расходуется на увеличение внутренней энергии, а какая – на совершение работы. Из уравнения 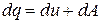 запишем
запишем
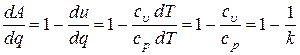 ,
,
где k – показатель адиабаты.
Для двухатомного газа показатель адиабаты k = 1,4, тогда
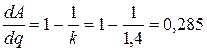 .
.
То есть меньше трети (0,285 или 28,5 %) подведенного тепла при изобарном процессе расходуется на совершение работы, остальное (71,5 %) идет на увеличение внутренней энергии газа.
Дата добавления: 2017-04-05; просмотров: 1684;











