Изотермический процесс
Изотермическим называется процесс, протекающий при постоянной температуре. Такой процесс практически реализовать достаточно трудно, ведь при совершении газом работы по преодолению внешних сил необходимо также отводить тепло от этого газа, чтобы не изменилась его температура (а значит и внутренняя энергия).
При T = constиз уравнения состояния получаем
 или или 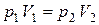 , ,
| (15) |
то есть, при постоянной температуре для данной массы газа произведение давления газа на его объем постоянно (закон Бойля – Мариотта). Графическое изображение изотермического процесса в координатах p – V представляет собой гиперболу (рис. 7).
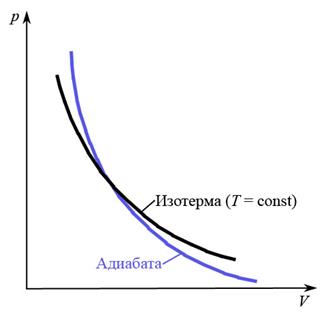
Рис. 7
При изотермическом процессе изменения внутренней энергии газа не происходит. Понятно, что для этого от газа нужно отводить тепло в количестве, эквивалентном работе, затрачиваемой извне на сжатие газа:
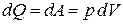 .
.
Работа 1 кг газа при изотермическом процессе определится выражением
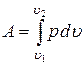 .
.
Зависимость давления от удельного объема получим из уравнения состояния
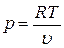 .
.
Подставляя это выражение в формулу для определения работы, получим
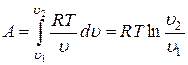 .
.
С учетом зависимостей 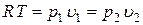 , а также
, а также 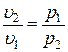 , можем записать
, можем записать
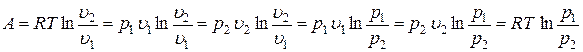 .
.
Адиабатный процесс
Адиабатным называют термодинамический процесс, протекающий без теплообмена рабочего тела (газа) с окружающей средой. Практически такой процесс можно реализовать, окружив сосуд с газом толстым слоем высококачественного теплоизоляционного материала. Кроме того, некоторые термодинамические процессы происходят настолько быстро, что за время процесса рабочее тело не успевает обменяться теплом с окружающей средой. Такие процессы тоже можно с определенной степенью приближения считать адиабатными.
Для адиабатного процесса первый закон термодинамики запишется так
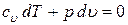 .
.
Продифференцируем уравнение состояния 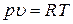 :
:
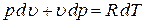
и выразим отсюда величину dT:
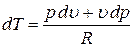 .
.
Подставим это значение в предыдущую формулу и после перегруппировки получим
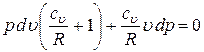 .
.
Вспомним уравнение Майера
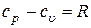 .
.
Тогда можно записать
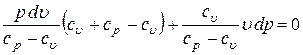 .
.
Продолжая преобразования, получаем
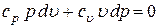 ;
;
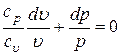 .
.
Ранее мы ввели обозначение 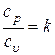 и отметили, что k – величина постоянная. Тогда последнее выражение можно проинтегрировать и получить
и отметили, что k – величина постоянная. Тогда последнее выражение можно проинтегрировать и получить
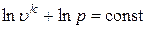 или
или 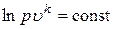 .
.
Окончательно можно записать
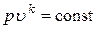 или или 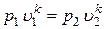 . .
| (16) |
Зависимости (16) есть уравнения адиабатного процесса. Величина k называется показателем адиабаты.
Используя уравнение состояния, можно получить связь других параметров в адиабатном процессе
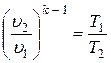 ;
;
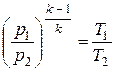 .
.
Кривую, отображающую адиабатный процесс в координатах p – V, называют адиабатой (рис. 7). Так как 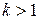 , то при изменении объема в адиабатном процессе изменение давления идет более интенсивно, чем в изотермическом, то есть адиабата поднимается более круто, чем изотерма.
, то при изменении объема в адиабатном процессе изменение давления идет более интенсивно, чем в изотермическом, то есть адиабата поднимается более круто, чем изотерма.
При адиабатном процессе внешняя работа полностью выполняется за счет изменения внутренней энергии газа
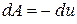 или
или 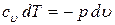 .
.
Для всего процесса работу можно определить как
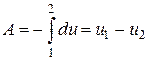 ,
,
или
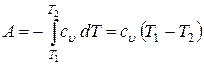 .
.
Здесь мы считали 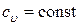 .
.
Работу 1 кг газа при адиабатном процессе можно посчитать и несколько иначе. Поскольку 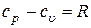 и
и 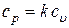 , то можно записать
, то можно записать
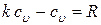 ;
;
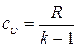 ;
;
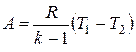 .
.
С учетом того, что 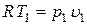 и
и 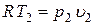 получим
получим
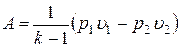 .
.
Можно получить еще несколько формул для работы газа.
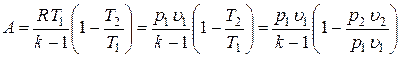 .
.
Вспомним, что 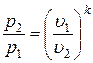 и
и 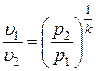 . Тогда
. Тогда
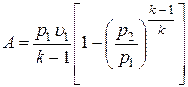 ;
;
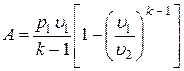 ;
;
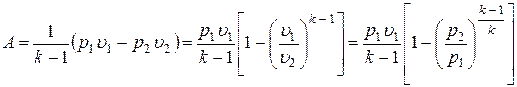 .
.
Дата добавления: 2017-04-05; просмотров: 2317;











