Распределение напряжений в грунтовом основании

<10 11 121314 15 16 >

При определении напряжений в грунтах грунты рассматриваются как линейно-деформируемые тела в стабилизированном состоянии, у которых вся нагрузка уже передалась на скелет грунта.

Для определения напряжений в грунтах используется принцип линейной зависимости между напряжениями и деформациями с учетом добавочных условий, вытекающих из физической природы грунтов как дисперсных тел, например, изменения пористости при изменении давления по закону уплотнения и т. п.

При определении напряжений в грунтах уравнения теории линейно-деформируемых тел будут справедливы для напряжений, при которых отсутствуют области пластических деформаций под фундаментами, или при условии, что эти области имеют незначительную величину по сравнению со всей площадью загрузки. Для оснований сооружений обычно и назначают такую величину напряжений, чтобы под подошвой фундаментов не возникало областей пластических деформаций.

С учетом всех особенностей грунтовых оснований, при определении напряжений в массиве принимают, что грунт является сплошным линейно-деформируемым телом, испытывающим одноразовое загружение. При этих условиях для определения осредненных напряжений в точке массива грунта используют решения теории упругости.

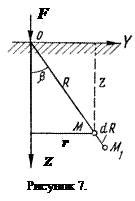Основная задача — действие сосредоточенной силы приложенной перпендикулярно к поверхности линейно-деформируемого полупространства. Задача распределения напряжений в любой точке массива от действия сосредоточенной силы F (рисунок 7) является основной в теории распределения напряжений в грунтах, впервые решение ее дано Буссинеском.

Составляющие напряжений в точке М для любой площадки, параллельной ограничивающей плоскости, при действии на поверхность линейно-деформируемого массива сосредоточенной силы (рисунок 8) определяются формулами

,
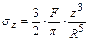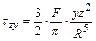,	(22)
,

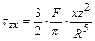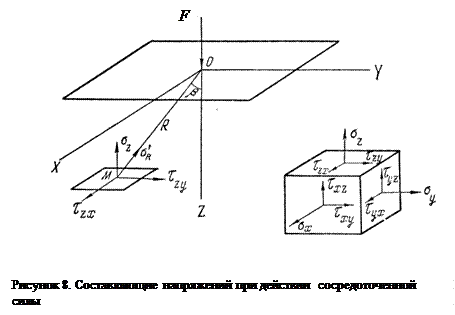
где R – расстояние от точки приложения силы F до рассматриваемой точки М;

x, y и z – координаты точки М.

В рассматриваемой задаче напряжения s_z на глубине z в точке М равны напряжениям s_z для любой точки расположенной на окружности радиуса r с координатой z (рисунок 7). Поэтому часто формулу для напряжений s_z записывают в виде

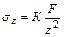(23)

где .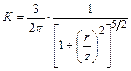

Действие равномерно распределенной нагрузки.Если на поверхности грунтового массива приложено местное распределенное давление, то для определения напряжений в толще массива поступают следующим образом: выделяют бесконечно малый элемент загруженной площади и, считая нагрузку на этот элемент сосредоточенной, пользуясь формулами (22), определяют составляющие напряжений. Проинтегрировав полученные выражения в пределах всей площади получают формулы для составляющих напряжений от действия данной нагрузки.

При равномерно распределенном давлении, после интегрирования по прямоугольной площади загружения (рисунок 9), вертикальные нормальные напряжения s_zр для точек, расположенных под центром прямоугольной площади загружения с координатой z, определяются выражением

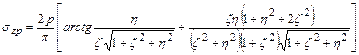(24)

где h = l/b; z =2z/b.

При равномерно распределенном давлении после интегрирования по полосовой площади загружения (ленточные фундаменты) вертикальные нормальные напряжения s_zр для точек, расположенных под центром полосовой площади загружения с координатой z, определяются выражением

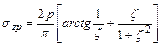(25)

где z =2z/b.

Поскольку напряжения s_zр зависят от р и безразмерных величин z и h, для удобства вычислений формулы (24) и (25) преобразованы к виду

s_zp = a×p,

(26)

где 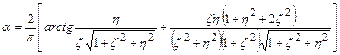для прямоугольной площадки и 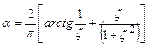для полосовой нагрузки.

Коэффициенты a в зависимости от размеров z и h сведены в таблицу 17.

Таблица 17

z=2z/b (z=z/b)	Коэффициент a для фундаментов
круг- лых	прямоугольных с соотношением сторон h=l/b, равным	ленточ- ных
		1,0	1,4	1,8	2,4	3,2		(h³10)
0,4 0,8 1,2 1,6 2,0 2,4 2,8 3,2 3,6 4,0 4,4 4,8 5,2 5,6 6,0 6,8 7,6 8,4 9,2 10,4 12,0	1,000 0,949 0,756 0,547 0,390 0,285 0,214 0,165 0,130 0,106 0,087 0,073 0,062 0,053 0,046 0,040 0,031 0,024 0,021 0,017 0,014 0,010	1,000 0,960 0,800 0,606 0,449 0,336 0,257 0,201 0,160 0,131 0,108 0,091 0,077 0,067 0,058 0,051 0,040 0,032 0,026 0,022 0,019 0,013	1,000 0,972 0,848 0,682 0,532 0,414 0,325 0,260 0,210 0,173 0,145 0,123 0,105 0,091 0,079 0,070 0,055 0,044 0,037 0,031 0,024 0,018	1,000 0,975 0,866 0,717 0,578 0,463 0,374 0,304 0,251 0,209 0,176 0,150 0,130 0,113 0,099 0,087 0,064 0,056 0,046 0,039 0,031 0,023	1,000 0,976 0,876 0,739 0,612 0,505 0,419 0,349 0,294 0,250 0,214 0,185 0,161 0,141 0,124 0,110 0,088 0,072 0,060 0,051 0,040 0,031	1,000 0,977 0,879 0,749 0,629 0,530 0,449 0,383 0,329 0,285 0,248 0,218 0,192 0,170 0,152 0,136 0,110 0,091 0,077 0,065 0,052 0,040	1,000 0,977 0,881 0,754 0,639 0,545 0,470 0,410 0,360 0,319 0,285 0,255 0,230 0,208 0,189 0,173 0,145 0,123 0,105 0,091 0,074 0,058	1,000 0,977 0,881 0,755 0,642 0,550 0,477 0,420 0,374 0,337 0,306 0,280 0,258 0,239 0,223 0,208 0,185 0,166 0,150 0,137 0,122 0,106

Коэффициент a для промежуточных значений z и h вычисляется линейной интерполяцией.

Формула (26) является основной рабочей формулой для вычисления напряжений в толще грунтового основания от действия равномерно распределенных давлений по прямоугольной и полосовой площадям.

Выражениями (24) и (25) пользуются в том случае, если размер z превышает данные таблицы 17.

Нормальные вертикальные напряжения на глубине z от прямоугольной площади загружения по вертикали, проходящей через угловую точку площади, например, точку С (рисунок 9), обозначаются s_zp_,c и определяются по формуле

s_z_p_,c = 0,25×a×p,

(27)

где a - коэффициент, принимаемый по таблице 17 в зависимости от соотношения сторон прямоугольной площади h и относительной глубины, равной x =z/b.

Нормальные вертикальные напряжения, получаемые по формулам (23)-(27) являются сжимающими напряжениями. В механике грунтов и при проектировании оснований фундаментов (но не самих конструкций фундаментов) нормальные вертикальные сжимающие напряжения считаются положительными.

<10 11 121314 15 16 >

Дата добавления: 2017-04-05; просмотров: 5536;